Заметим, что

-12(mod 7) º -5(mod 7) º 2(mod 7) º 9(mod 7) и т.д.

 Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(a + b) mod n = [a(mod n) + b(mod n )] mod n,

(a - b) mod n = [a(mod n) - b(mod n )] mod n,

(a * b) mod n = [a(mod n) * b(mod n )] mod n,

[a * (b + c)] mod n = {[a * b(mod n)] + [a * c(mod n)]} mod n.

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.

Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа а по модулю n

a^x mod n

можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

a⁸ mod n,

 не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

(a * a * a * a * a * a * a * a) mod n

 Вместо этого выполняют три малых умножения и три малых приведения по  модулю:

((a² mod n)² mod n)² mod n.

 Тем же способом вычисляют

a¹⁶ mod n = (((a² mod n)² mod n)²mod n)² mod n.

 

Вычисление

a^x mod n.

 где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х как сумму степеней 2:

x = 25₍₁₀₎ ® 1 1 0 0 1₍₂₎, поэтому 25 = 2⁴+ 2³ + 2⁰

Тогда

a²⁵ mod n = (a * a²⁴) mod n = (a * a⁸ * a¹⁶) mod n = a * ((a²)²)² * (((a²)²)²)² mod n = ((((a² * a)²)²)² * a) mod n.

 При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a² mod n) * a) mod n)² mod n)² mod n)² mod n) * a) mod n

 Этот метод уменьшает трудоемкость вычислений до 1,5xk операций в среднем, где k-длина числа в битах [123].

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.

 

 

Алгоритм Евклида для нахождения наибольшего общего делителя

 Целое число а делит без остатка другое целое число b, если, и только если

b = k * a

для некоторого целого числа k. В этом случае число а называют делителем числа b или множителем в разложении числа b на множители.

Пусть а - целое число, большее 1. Тогда а является простым числом, если его единственными положительными делителями будут 1 и само а, в противном случае а называется составным.

Любое целое n >1 может быть представлено единственным образом с точностью до порядка сомножителей как произведение простых [45].

Существенный с точки зрения криптографии факт состоит в том, что не известно никакого эффективного алгоритма разложения чисел на множители; не было получено и никакой нетривиальной нижней оценки временной сложности разложения. Никаких эффективных методов не известно даже в таком простом случае, когда необходимо восстановить два простых числа р и q из их произведения:

n = p * q

Наибольший общий делитель чисел а и b, обозначаемый как ПОД (а, b) или просто (а, b),-это наибольшее целое, делящее одновременно числа а и b. В эквивалентной форме (а, b)-это то  единственное натуральное число, которое делит а и b и делится на любое целое, делящее и а и b. Если НОД (а, b)=1, то целые а и b- взаимно простые.

Наибольший общий делитель может быть вычислен с помощью алгоритма Евклида. Евклид описал этот алгоритм в своей книге "Начала", написанной около 300 лет до н.э. Он не изобрел его. Историки полагают, что этот алгоритм, возможно, старше еще на 200 лет. Это древнейший нетривиальный алгоритм, который просуществовал до настоящего времени и все еще хорош и сегодня.

Опишем алгоритм Евклида для нахождения НОД (а, b). Введем обозначения: q_i -частное; r_i-остаток. Тогда алгоритм можно представить в виде следующей цепочки равенств:

 

 

Остановка гарантируется, поскольку остатки r_i от делений образуют строго убывающую последовательность натуральных чисел. Из этой цепочки немедленно получаем, что r_kесть общий делитель чисел а и b и, более того, что любой общий делитель чисел а и b делит и r_k. Таким образом, r_k=HOД(a, b) или r_k =(a, b).

 Алгоритм Евклида для вычисления наибольшего общего делителя

 

 

 Вычисление обратных величин

 В арифметике действительных чисел нетрудно вычислить мультипликативную      обратную величину а~1 для ненулевого а:

a^-1 = 1/a или a * a^-1 =1

Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку

 

 

В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения

4 * x º 1(mod 7)

 эквивалентно нахождению таких значений х и k, что

4 * x º 7 * k +1

где х и k-целые числа.

Общая формулировка этой задачи -нахождение такого целого числа х, что

a * x(mod n) = 1

Можно также записать

a^-1 º x(mod n)

 Решение этой задачи иногда существует, а иногда его нет. Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку

5 * 3 = 15 º 1(mod 14).

 С другой стороны, число 2 не имеет обратной величины по модулю 14.      

Вообще сравнение

a^-1 º x(mod n)

 имеет единственное решение, если а и n - взаимно простые числа.

Если числа а и n не являются взаимно простыми, тогда сравнение

не имеет решения [45].

a^-1 º x(mod n)]

 Сформулируем основные способы нахождения обратных величин. Пусть целое число а Î{0,1,2,..., n-1}. Если НОД(а, n)=1, то a * i (mod n) при 1 = 0,1,2,...,n-1 является перестановкой множества {0,1,2, ...,n-1}.

Например, если а=3 и n=7(НОД(3,7}=1), то

3 * i (mod 7) при i = 0,1,2,…,6

 является последовательностью 0, 3, 6, 2, 5, 1, 4, т.е. перестановкой множества (0,1,2, ...,6).

Это становится неверным, когда НОД(а, n)¹1. Например, если а=2 и n= 6, то

Если НОД(а, n) = 1, тогда существует обратное число а^-1, 0<а^-1<n, такое, что

a * a^-1 º 1(mod n)

 Действительно, a * i(mod n) является перестановкой 0,1,..., n-1, поэтому существует i, такое, что

a * i º 1(mod n).

 Как уже отмечалось, набор целых чисел от 0 до n-1 называют полным набором вычетов по модулю п. Это означает, что для любого целого числа а(а>0) его вычет r = a(mod n)-это некоторое целое число в интервале от 0 до n-1.

Выделим из полного набора вычетов подмножество вычетов, взаимно простых с п. Такое подмножество называют приведенным набором вычетов.

Пример. Пусть модуль n=11- простое число. Полный набор вычетов по модулю 11.

(0,1,2,…,10)

 

При формировании приведенного            набора вычетов из них удаляется только один элемент-0. Приведенный набор вычетов по модулю 11 имеет 11-1=10 элементов.

Вообще приведенный набор вычетов по модулю простого числа n имеет n-1 элементов.

Пример. Пусть модуль n=10. Полный набор вычетов по модулю n =10

{0,1,2,3,4,5,6,7,8,9}.                                                            

Из них только 1, 3, 7, 9 не имеют общего сомножителя с числом 10. Поэтому приведенный набор вычетов по модулю 10 равен {1, 3, 7, 9}. При формировании этогоприведенного набора были исключены элементы:

0                   (1 элемент),

кратные 2       (4 элемента),

кратные 5       (1 элемент),

т.е. всего шесть элементов. Вычитая их из 10, получаем 10-1-4-1=4. т.е. четыре элемента в приведенном наборе.

10. Асимметричные шифры. Свойства, принципы построения.

Криптографическая система с открытым ключом (также асимметричное шифрование, асимметричные шифры) — система шифрования и/или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифрования сообщения используется секретный ключ. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.

Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значение f(x), тогда как определение xиз f(x) сложно в смысле теории.

Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой y, что зная f(x), можно вычислить x. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.

Понять идеи и методы криптографии с открытым ключом помогает следующий пример — хранение паролей в компьютере. Каждый пользователь в сети имеет свой пароль. При входе, он указывает имя и вводит секретный пароль. Но если хранить пароль на диске компьютера, то кто-нибудь его может считать (особенно легко это сделать администратору этого компьютера) и получить доступ к секретной информации. Для решения задачи используется односторонняя функция. При создании секретного пароля в компьютере сохраняется не сам пароль, а результат вычисления функции от этого пароля и имени пользователя. Например, пользователь Алиса придумала пароль «Гладиолус». При сохранении этих данных вычисляется результат функции f(ГЛАДИОЛУС), пусть результатом будет строкаРОМАШКА, которая и будет сохранена в системе. В результате файл паролей примет следующий вид:

Вход в систему теперь выглядит так:

Когда Алиса вводит «секретный» пароль, компьютер проверяет, даёт или нет функция, применяемая к ГЛАДИОЛУС, правильный результат РОМАШКА, хранящийся на диске компьютера. Стоит изменить хотя бы одну букву в имени или в пароле, и результат функции будет совершенно другим. «Секретный» пароль не хранится в компьютере ни в каком виде. Файл паролей может быть теперь просмотрен другими пользователями без потери секретности, так как функция практически необратимая.

Основные принципы построения криптосистем с открытым ключом

1. Начинаем с трудной задачи P. Она должна решаться сложно в смысле теории: не должно быть алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P за полиномиальное время относительно размера задачи. Более правильно сказать: не должно быть известного полиномиального алгоритма, решающего данную задачу — так как ни для одной задачи ещё пока не доказано, что для неё подходящего алгоритма нет в принципе.

2. Можно выделить легкую подзадачу P' из P. Она должна решаться за полиномиальное время, лучше, если за линейное.

3. «Перетасовываем и взбалтываем» P', чтобы получить задачу P'', совершенно не похожую на первоначальную. Задача P'', по крайней мере, должна выглядеть как оригинальная труднорешаемая задача P.

4. P'' открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из P'' получить P', держится в секрете как секретная лазейка.

5. Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как второй решает P'' задачу, первый использует секретную лазейку и решает P' задачу.

Особенности системы

Применение:

Алгоритмы криптосистемы с открытым ключом можно использовать

• Как самостоятельные средства для защиты передаваемой и хранимой информации.

• Как средства распределения ключей. Обычно с помощью алгоритмов криптосистем с открытым ключом распределяют ключи, малые по объёму. А саму передачу больших информационных потоков осуществляют с помощью других алгоритмов.

• Как средства аутентификации пользователей.

Преимущества:

• Преимущество асимметричных шифров перед симметричными шифрами состоит в отсутствии необходимости предварительной передачи секретного ключа по надёжному каналу.

• В симметричной криптографии ключ держится в секрете для обеих сторон, а в асимметричной криптосистеме только один секретный.

• При симметричном шифровании необходимо обновлять ключ после каждого факта передачи, тогда как в асимметричных криптосистемах пару (E,D) можно не менять значительное время.

• В больших сетях число ключей в асимметричной криптосистеме значительно меньше, чем в симметричной.

Недостатки:

• Преимущество алгоритма симметричного шифрования над несимметричным заключается в том, что в первый относительно легко внести изменения.

• Хотя сообщения надежно шифруются, но «засвечиваются» получатель и отправитель самим фактом пересылки шифрованного сообщения.

• Несимметричные алгоритмы используют более длинные ключи, чем симметричные. Ниже приведена таблица, сопоставляющая длину ключа симметричного алгоритма с длиной ключа несимметричного алгоритма с аналогичной криптостойкостью: 

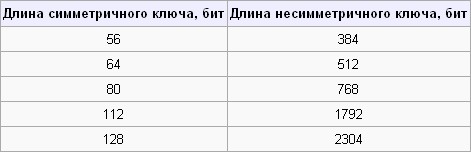
• Процесс шифрования-расшифрования с использованием пары ключей проходит на два-три порядка медленнее, чем шифрование-расшифрование того же текста симметричным алгоритмом.

• В чистом виде асимметричные криптосистемы требуют существенно больших вычислительных ресурсов, потому на практике используются в сочетании с другими алгоритмами.

  1. Для ЭЦП сообщение предварительно подвергается хешированию, а с помощью асимметричного ключа подписывается лишь относительно небольшой результат хеш-функции.

  2. Для шифрования они используются в форме гибридных криптосистем, где большие объёмы данных шифруются симметричным шифром на сеансовом ключе, а с помощью асимметричного шифра передаётся только сам сеансовый ключ.

Схема шифрования с открытым ключом

Пусть K — пространство ключей, а e и d — ключи шифрования и расшифрования соответственно. E_e — функция шифрования для произвольного ключа e K, такая что:

E_e(m) = c

Здесь c C, где C — пространство шифротекстов, а m M, где M — пространство сообщений.

D_d — функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифротекст c:

D_d(c) = m

{E_e: e K} — набор шифрования, а {D_d: d K} — соответствующий набор для расшифрования.

Каждая пара (E,D) имеет свойство: зная E_e, невозможно решить уравнение E_e(m) = c, то есть для данного произвольного шифротекста c C, невозможно найти сообщение m M. Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E_e является односторонней функцией, а d — лазейкой.

Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемыми Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.

1. Боб выбирает пару (e,d) и шлёт ключ шифрования e (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу, либо его подлинность должна быть гарантирована некоторым сертифицирующим органом).

2. Чтобы послать сообщение m Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e: E_e(m) = c, c — полученный шифротекст.

3. Боб расшифровывает шифротекст c, применяя обратное преобразование D_d, однозначно определённое значением d.

Функция, которая удовлетворяет все свойства называется функцией с открытыми дверями.

Теоретико-числовые задачи.

Факторизация большого целого числа

Описание задачи

Пусть дано целое число N >1, которое не является простым, тогда существует целое число a , такое, что 1 < a < N и a | N . Задача состоит в том, что бы найти такое a или доказать, что оно равно 1. В криптографических приложениях используют число N , состоящее из двух простых множителей соизмеримой величины, другими словами они имеют соизмеримые двоичные длины.

Дискретный логарифм

В данном случае под задачей дискретного логарифма подразумевается целый класс задач, которые отличаются друг от друга лишь алгебраическими структурами, образующими группы. Далее дадим наиболее общее определение данной задачи. Пусть дана конечная циклическая группа G порядка n , образующий элемент P и произвольный элемент группы Q . Задача нахождения дискретного логарифма состоит в поиске такого целого числа x , что Q = xP .

Отметим, что это число приведено по модулю n . Рассмотрим задачи дискретного логарифмирования (DLP) на конкретных алгебраических структурах, которые образуют группы.

Постквантовая криптография-разработка неизвестных алгоритмов.

Квантовый алгоритм — это алгоритм, предназначенный для выполнения на квантовом компьютере.

Квантовый алгоритм представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами их надо совершать. Квантовый алгоритм задается либо в виде словесного описания таких команд, либо с помощью их графической записи в виде системы вентилей (quantum gate array).

Результат работы квантового алгоритма носит вероятностный характер^[1]. За счёт небольшого увеличения количества операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.

Множества задач, допускающих решение на квантовом компьютере и на классическом, совпадают. Квантовый компьютер, таким образом, не увеличивает число алгоритмически разрешимых задач. Весь смысл применения квантового компьютера в том, что некоторые задачи он способен решить существенно быстрее, чем любой из классических. Для этого квантовый алгоритм должен по ходу вычисления генерировать и использовать запутанные квантовые состояния (см. Квантовая суперпозиция и Квантовая сцепленность).

Любая задача, решаемая квантовым алгоритмом, может быть решена и классическим компьютером путем прямого вычисления унитарных матриц экспоненциальной размерности, получения явного вида квантовых состояний. В частности, проблемы, неразрешимые на классических компьютерах (например, проблема остановки), остаются неразрешимыми и на квантовых. Но такое прямое моделирование требует экспоненциального времени, и потому возникает возможность, используя квантовый параллелизм, ускорять на квантовом компьютере некоторые классические алгоритмы^[2].

Дискретное логарифмирование (DLOG) — задача обращения функции   в некоторой конечной мультипликативной группе  .

Наиболее часто задачу дискретного логарифмирования рассматривают в мультипликативной группе кольца вычетов или конечного поля, а также в группе точекэллиптической кривой над конечным полем. Эффективные алгоритмы для решения задачи дискретного логарифмирования в общем случае неизвестны.

Для заданных g и a решение x уравнения   называется дискретным логарифмом элемента a по основанию g. В случае, когда G является мультипликативной группой кольца вычетов по модулю m, решение называют также индексом числа a по основанию g. Индекс числа a по основанию g гарантированно существует, если gявляется первообразным корнем по модулю m.