26. Непрерывная случайная величина, законы распределения.

НЕПРЕРЫВНОЙ случайной величиной называется случайная величина, которая принимает ЛЮБОЕ ЗНАЧЕНИЕ НА НЕКОТОРОМ (возможно и бесконечном) ИНТЕРВАЛЕ

Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу­бесконечными или бесконечными, например: (a; b], (–µ ; a), [b;µ), (–µ; µ).

Законами распределения непрерывных случайных величин называют плотности распределений.

«Законы распределения непрерывных случайных величин»

 

1. Показательный закон распределения.

2. Нормальный закон распределения.

3. Нормальная кривая.

4. Правило трех сигм.

 

 

1.  Показательный закон  распределения.

Непрерывная случайная величина   имеет показательный закон распределения с параметром  , если ее плотность вероятности имеет вид:

Функция распределения случайной величины  , имеющей показательный закон распределения, равна:

ее математическое ожидание   ,   дисперсия:   

   

2. Нормальный закон распределения.

Нормальным называют распределение вероятностей непрерывной случайной величины  , которое описывается плотностью 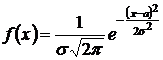 , где   - математическое ожидание;   - среднееквадратическое отклонение случайной величины  .

 

3. Нормальная кривая.

Кривая    имеет вид, изображенный на рисунке. Эта  кривая называется кривой Гаусса

Вероятность того, что   примет значения, принадлежащее интервалу  :

где  функция Лапласа.

Значения функции Лапласа находятся по таблицам.

Вероятность того, что абсолютная  величина отклонения меньше положительного числа  , может быть  вычислена по формуле  .

В частности, при а=0 справедливо равенство    

Медианой  М_е(Х) называют то возможное значение   , при котором ордината   делит пополам площадь, ограниченную кривой распределения. Так как нормальная кривая (график функции  ) симметрична относительно прямой  , то ордината   делит пополам площадь, ограниченную нормальной кривой, значит,   .

Модой    называют то возможное значение  ,  при котором  дифференциальная функция имеет максимум.

Мода и медиана для нормального распределения совпадают с математическим  ожиданием.

 

4. Правило «трех сигм».

Если случайная величина   имеет нормальный закон распределения с параметрами   и  , т.е.  , то практически достоверно, что ее значения заключены в интервале  :

 

27. Непрерывная случайная величина, её числовые характеристики.

Числовые характеристики непрерывных случайных величин»

 

1. Математическое ожидание непрерывной случайной  величины.

2.  Дисперсия непрерывной случайной  величины.

3.  Мода и медиана случайной величины.

4.  Закон равномерного распределения.

 

 

1. Математическое ожидание непрерывной случайной величины.

Математическим  ожиданием  непрерывной  случайной величины  , возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

   

Если возможные значения принадлежат всей оси  , то 

 

  

2. Дисперсия непрерывной  случайной величины.

Дисперсией непрерывной случайной величины   называют математическое ожидание квадрата ее отклонения.

Если возможные значения   принадлежат отрезку   , то

если возможные значения принадлежат всей оси х, то

Для вычислений более удобны формулы:

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для  величины дискретной, равенством   .

Замечание 1. Свойства математического ожидания и дисперсии дискретных  случайных  величин сохраняются и для  непрерывных  случайных  величин.