4. Множества и подмножества.

Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое.

Под множеством понимается некоторая совокупность объектов, объединенных по какому-то общему признаку.

 Отдельные объекты, из которых состоит множество, называются элементами множества.

Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b, c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:

                  N - множество всех натуральных чисел;                   Z - множество всех целых чисел;                   Q - множество всех рациональных чисел;                   R - множество всех действительных чисел;                   C - множество всех комплексных чисел;                   Z₀ - множество всех неотрицательных целых чисел.

Запись   (или  ) означает, что элемент a принадлежит множеству A.

Запись   (или  ) означает, что элемент a не принадлежит множеству A.

Подмно́жество в теории множеств - это понятие части множества.

Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают   (или  )

               

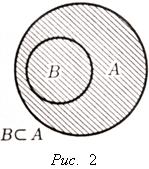
Всегда  , так как каждый элемент множества, естественно, принадлежит A. Пустое множество, т. е. множество, не содержащее ни одного элемента, обозначим символом  . Любое множество содержит пустое множество в качестве своего подмножества.

Если  , то A и B называются равными множествами, при этом записывают A = B.

5. Операции над множествами: объединение множеств, свойства этой операции.

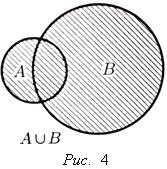
Объединение множеств А и В — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т.е. принадлежат А или принадлежат В.

объединением множеств A и B называется множество

               

6. Операции над множествами: пересечение множеств, свойства этой операции.

Пересечение множеств А и В — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В.

Пересечением подмножеств A и B называется множество

               

7. Элементы комбинаторики: Перестановки.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.

Правило суммы: пусть имеется n попарно непересекающихся множеств A₁, A₂, …, A_n , содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m₁ + m₂ + … + m_n.

Пример. Если на первой полке стоит X книг, а на второй Y, то выбрать книгу с первой или второй полки, можно X+Y способами.

Правило произведения: пусть имеется n множеств A₁, A₂, …, A_n содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а₁, а₂, ..., а_n), где а_i  А _i1 (i = 1, 2, …, n), равно m₁ · m₂ · … · m_n.

Пример. Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

Факториал. Так называют часто встречающуюся в практике функцию, определенную для целых неотрицательных чисел. Название функции происходит от английского математического термина factor - «сомножитель». Обозначается она  . Для каждого целого положительного числа   функция   равна произведению всех целых чисел от 1 до  . Например:  . Для удобства полагают по определению  . Особенно часто встречается факториал в комбинаторике. Например, количество способов выстроить   школьников в одну шеренгу равняется 

Определение. Если в некотором множестве   переставлять местами элементы, оставляя неизменным их количество, то каждая полученная таким образом комбинация называется перестановкой.

 Общее число перестановок из m элементов обозначается P_m и вычисляется по формуле: