3. Мода и медиана случайной величины.

Медианой   называют такое возможное значение, при котором ордината   делит пополам площадь, ограниченную кривой распределения, т.е. такое значение, для которого  . 

Модой    называют ее наиболее вероятное значение  , при котором дифференциальная функция имеет максимум.

 

4. Закон равномерного распределения.

Равномерным называется такое распределение вероятностей  непрерывной  случайной величины Х, если на интервале (а, в), которому принадлежат все возможные значения Х, дифференциальная функция сохраняет постоянное значение, а именно  ; вне этого интервала 

                      

Таким образом:  

 

28. Непрерывная случайная величина, графическое представление её законов распределения.

1. График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения σ.

Асимметрия, эксцесс, мода и медиана нормального распределения равны: As(X) = 0; Ex(X) = 0; Mo(X) = a; Me(X) = a, где а - математическое ожидание. Интегральная функция нормального распределения вероятностей:

2. Плотность вероятности равномерного распределения сохраняет на интервале (a, b) постоянное значение, вне этого интервала плотность вероятности равна нулю. Исходя из основного свойства плотности вероятности, f(x) = 1/(b-a) на интервале (a;b). Интегральную функцию распределения (вероятность того, что с.в. примет значение меньшее, чем x) находим как интеграл от -∞ до x от плотности вероятности: F(x) = (x-a)/(b-a) Графики плотности вероятности и функции равномерного распределения:

Математическое ожидание равномерного распределения: M(X) = (a + b)/2 Дисперсия равномерного распределения: D(X) = (b - a)²/12 Среднее квадратичное отклонение равномерного распределения: σ(X) = (b - a)/(2√3)

29. Нормально распределенная случайная величина, её законы распределения, числовые характеристики и графическое представление.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью  . Нормальное распределение задается двумя параметрами:   – математическим ожиданием,   – средним квадратическим отклонением. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Нормированным называют нормальное распределение с параметрами  . Плотность нормированного распределения задается формулой .

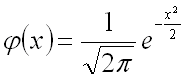Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2. Плотность распределения имеет вид: 

Построим график:

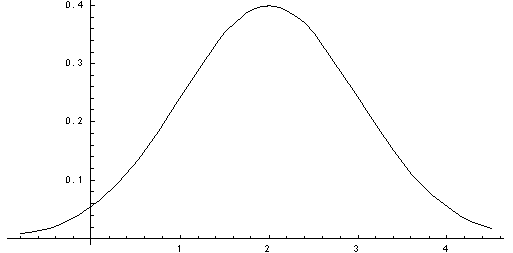
Найдем вероятность попадания случайной величины в интервал (1; 3). 

Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2. 

Тот же результат может быть получен с использованием нормированной функции Лапласа. 

Функция Лапласа.

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.   Обозначим   Тогда 

Т.к. интеграл   не выражается через элементарные функции, то вводится в рассмотрение функция  , которая называется функцией Лапласа или интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. Ниже показан график функции Лапласа

. 

 

Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0; 2) Ф(-х) = - Ф(х); 3) Ф¥) = 1. Функцию Лапласа также называют функцией ошибок и обозначают erf x. Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением: 

Ниже показан график нормированной функции Лапласа.

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:  Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:   Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.