Правило сложения векторов по правилу треугольников:
Требуется
найти сумму данных векторов. В силу
того, что все векторы считаются свободными,
отложим вектор
от
конца вектора
:
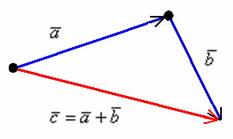Суммой
векторов
и
является
вектор
.
Свойства сложения векторов.
1. Сложение векторов подчиняется закону ассоциативности: (a+b)+c = a+(b+c)
2. Существует нулевой элемент относительно сложения векторов: a+(-a) = (-a)+a =0
3. Для любого вектора существует противоположный ему вектор, такой, что a+(-a)=(-a)+a=0
4. Сложение векторов подчиняется закону коммутативности: а+b =b+a
5.Первое распределительное свойство .(a+b)*c = a*c+b*c .
Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор с и будет являться разностью векторов а и b. Таким образом,
с = а − b = а + (− b).
Любой вектор ⃗𝑝 можно разложить, и притом единственным образом, по двум данным неколлинеарным векторам ⃗𝑎 и ⃗𝑏
⃗𝑝 = 𝑥⃗𝑎 + 𝑦⃗𝑏.
1. В треугольнике 𝐴𝐵𝐶 медианы 𝐴𝑀 и 𝐶𝑁 пересекаются в точке 𝑂. Разложите по базисным векторам ⃗𝑚 = 𝑂𝐴 и ⃗𝑛 = 𝑂𝐶 следующие векторы: 𝑂𝑁, 𝐴𝐶, 𝐵𝐴, 𝐵𝑂.
2. В прямоугольнике 𝐴𝐵𝐶𝐷 точка 𝐹 делит сторону 𝐵𝐶 в отношении 2 : 3, считая от 𝐵. Разложите
𝐴𝐹 по 𝐵𝐴 и 𝐷𝐴.
3. В правильном шестиугольнике 𝐴𝐵𝐶𝐷𝐸𝐹 известно, что 𝐴𝐵 = ⃗𝑎, 𝐴𝐹 =⃗𝑏. Найдите векторы 𝐴𝐷, 𝐵𝐷, 𝐹𝐷 и 𝐵𝑀, где 𝑀 — середина стороны 𝐸𝐹.
13.
Скалярным произведением ⃗𝑎* ⃗b векторов ⃗𝑎 и ⃗b называется число (скаляр) равное произведению их длин (модулей), умноженному на соs угла между ними:
⃗𝑎* ⃗b = | ⃗𝑎|*| ⃗b|*cos(⃗𝑎, ⃗b).
Свойства скалярного произведения:
1) ⃗𝑎* ⃗b = ⃗b* ⃗a – коммутативность (переместительный закон);
2)( ⃗𝑎)* ⃗b = ( ⃗𝑎* ⃗b) –ассоциацивность относительно числового множителя(сочетательный закон);
3) ⃗𝑎*( ⃗b+¯с) = ⃗𝑎* ⃗b+ ⃗𝑎* ⃗с – дистрибутивность (распределительный закон);
4) ⃗𝑎* ⃗b= 0 – необходимое и достаточное условие перпендикулярности ненулевых векторов;
5) ⃗𝑎* ⃗а= ⃗𝑎2 = | ⃗a|2 – скалярный квадрат вектора.
14.
Векторным произведением ⃗𝑎* ⃗b векторов ⃗𝑎 и ⃗b называется вектор ⃗с, определяемый следующими условиями:
1.| ⃗c| = | ⃗𝑎|*| ⃗b|*sin(⃗𝑎, ⃗b).
2.Вектор ⃗с ортогонален каждому из векторов ⃗𝑎, ⃗b.
3.Векторы ⃗𝑎, ⃗b, ⃗с образуют правую тройку.
Свойства векторного произведения:
1) ⃗𝑎* ⃗b = - ⃗b* ⃗a – антикоммутативность ;
2)( ⃗𝑎)* ⃗b = ( ⃗𝑎* ⃗b) – ассоциацивность относительно числового множителя;
3) ⃗𝑎*( ⃗b+¯с) = ⃗𝑎* ⃗b+ ⃗𝑎* ⃗с – дистрибутивность ;
4) ⃗𝑎* ⃗b= 0 – необходимое и достаточное условие перпендикулярности ненулевых векторов;
15.
Смешанным произведением ⃗𝑎 ⃗b ⃗с векторов ⃗𝑎, ⃗b, ⃗с называется число, равное векторному произведению ⃗𝑎* ⃗b, умноженному скалярно на вектор ⃗с, т.е. ⃗𝑎 ⃗b ⃗с = (⃗𝑎* ⃗b)* ⃗с.
Геометрический смысл смешанного произведения. Модуль ⃗|𝑎 ⃗b ⃗с| равен объему параллелепипеда, построенного на векторах ⃗𝑎, ⃗b, ⃗с.
Свойства смешанного произведения:
1. ⃗𝑎 ⃗b ⃗с = ( ⃗𝑎* ⃗b)* ⃗с = ⃗𝑎*( ⃗b* ⃗с);
2. ⃗𝑎 ⃗b ⃗с = . ⃗b ⃗c ⃗a =. ⃗c ⃗a ⃗b = - ⃗b ⃗a ⃗с = - ⃗𝑎 ⃗c ⃗b;
3. ( ⃗𝑎) ⃗b ⃗с = ( ⃗𝑎 ⃗b ⃗с);
4. ⃗𝑎 ⃗b( ⃗с + ⃗d) = ⃗𝑎 ⃗b ⃗с + ⃗𝑎 ⃗b ⃗d;
5. ⃗𝑎 ⃗b ⃗с = 0 – необходимое и достаточное условие компланарности векторов ⃗𝑎, ⃗b, ⃗с.
16.
Уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.
Вид уравнения прямой в прямоугольной системе координат Oxy на плоскости задает теорема:
Всякое уравнение первой степени с двумя переменными x и y вида Ах +Ву+С =0, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида Ах +Ву+С =0 - называется общим уравнением прямой на плоскости.
Уравнение прямой вида y =k*x+b, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).
Определение углового коэффициента прямой дается через определение угла наклона прямой к положительному направлению оси Ox.
Углом наклона прямой к положительному направлению оси абсцисс в данной прямоугольной декартовой системе координат Oxy называют угол а, отсчитываемый от положительного направления оси Ох до данной прямой против хода часовой стрелки.
Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, k = tg a.
Параметрические
уравнения прямой на плоскости имеют
вид
,
где х 1 ,у 1, а
х и а у–
некоторые действительные числа, причем
а х и а у
одновременно не равны нулю, а -
параметр, принимающий любые действительные
значения.
Параметрические уравнения прямой устанавливают неявную зависимость между абсциссами и ординатами точек прямой линии с помощью параметра (отсюда и название этого вида уравнений прямой).
Пара чисел (х,у), которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра , представляет собой координаты некоторой точки прямой.
17.
Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, k = tg a.
Уравнение прямой с угловым коэффициентом имеет вид y =k*x+b,
Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y - y1 = k(x - x1).
Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка.
Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
Если в общем
уравнении прямой вида Ax+By
+C =0 числа А, В и С
таковы, что длина
вектора
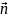= =(A,B) равна
единице, а C ≤ 0 , то это
общее уравнение прямой называется
нормальным уравнением прямой.
Нормальное уравнение прямой определяет
в прямоугольной системе координат Oxy
прямую линию, нормальным вектором
которой является вектор
= (A,B) ,
причем эта прямая проходит на расстоянии
|C| от начала координат в
направлении вектора
= (A,B).
Часто можно
видеть другую форму записи нормального
уравнения прямой: cosa
*x + cosb
*y – p = 0, где
cosa и
cosb -
действительные числа, представляющие
собой направляющие косинусы нормального
вектора прямой единичной длины (то
есть,
= (cosa,cosb)
и справедливо равенство |
|
=
),
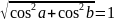а величина p (p ≥ 0 )
равна расстоянию от начала координат
до прямой.
18.
Расстояние
от точки M(x0;у0) до
прямой d:
Ax+By+C
=0 выражается формулой
.
Угол между двумя прямыми. Способ первый
Рассмотрим
две прямые, заданные уравнениями в общем
виде:
и не перпендикулярны, то ориентированный
угол q между ними
найдем по формуле:
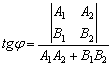
Самое пристальное
внимание обратим на знаменатель – это
в точности скалярное
произведение направляющих
векторов прямых:
Способ второй
Если прямые
заданы уравнениями с угловым коэффициентом
и
не перпендикулярны, то ориентированный
угол
между
ними найдем по формуле:
Условие перпендикулярности прямых выражается равенством 1+k1k2 = 0, откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых:k1 = -1/k2 , которая используется в некоторых задачах.
Есть и третий
способ решения. Идея состоит в том, чтобы
вычислить угол между направляющими
векторами прямых с помощью формулы:
.
Здесь результат заведомо будет
положительным. Но может получиться
тупой угол. В этом случае придётся из
180-ти градусов вычитать получившийся
арккосинус.
19.
Эллипсом
– называется геометрическое место
точек на плоскости, сумма расстояний
которых до двух заданных точек, называемых
фокусами, есть, величина постоянная,
большая чем расстояние между фокусами.
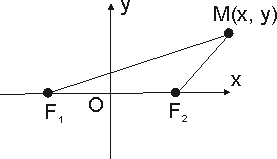
Комментарии
к определению: F1
и F2
– фокусы, | F1F2
|
= 2·с
— расстояние между фокусами, | MF1
| + |MF2|
= 2·a
>2·c
— определение эллипса.
Система
координат, в которой уравнение имеет
наиболее простой вид, называется
канонической. Проведём
ось абсцисс через фокусы, начало координат
поместим в середине между фокусами, ось
ординат направим перпендикулярно. Пусть
М(х,
у)
— произвольная точка на эллипсе, тогда
F1(-
c;
0) и F2(c;
0). Расстояния текущей точки эллипса до
её фокусов называются фокальными
расстояниями |MF1|
= r1,
|MF2|
= r2
и, по определению эллипса, имеем r1
+ r2
= 2·a.
Воспользовавшись
формулой расстояния между двумя точками,
из определения эллипса имеем:
+
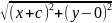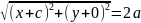
Избавимся
от иррациональности, возведя обе части
соотношения
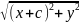=2а-
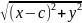
в
квадрат:
,
,
,
,
,
,
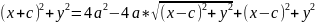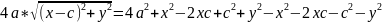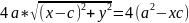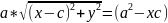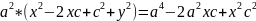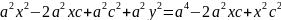далее
х2(а2
-
с2)
+ а2у2
= а2(а2
– с2),
а2
– с2
= b2
, x2b2
+a2y2
= a2b2.
Разделив
обе части на a2b2,
получим каноническое уравнение эллипса
.
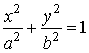