9)Условия работы см в простейшей системе при скорости отличной от синхронной. Понятие асинхронного режима. Применение метода наложения. Синхронный и асинхронный моменты см.

12

2

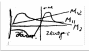
10. Элементарная теория статической устойчивости. Математические основы анализа статической устойчивости простейшей ЭЭС и ее состояния равновесия. Уравнения возмущенного движения. Уравнения первого приближения и анализ состояний равновесия. Виды нарушения устойчивости.

Нарушения устойчивости бывают апериодическими или колебательными.

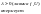
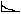
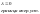
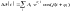
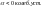
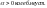
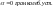
11. Статическая устойчивость одномашинной системы. Уравнения первого приближения. Характеристическое уравнения и его корни. Виды нарушения устойчивости. Позиционаня модель и условия устойчивости.

Статическая устойчивость – способность системы сохранять (восстанавливать) исходный (или близкий к нему) режим при действии «малых» возмущений.

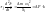
При анализе рассматриваем только малые отклонения скорости ротора от синхронной:

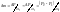
При отличии скорости вращения ротора от синхронной у машины появляются асинхронные свойства:

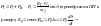
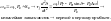_{Малым возмещениям соответствуют малые начальные отклонения:}

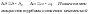
Чтобы решение было устойчивым, то действительная часть корней должна быть <0.

Нарушения устойчивости бывают апериодическими или колебательными.

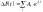
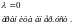
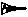
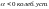
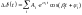
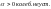
Синхронизирующие мощности(д.б.>0) : С1. Без АРВ С2.АРВПДС3. АРВ сильного действия

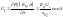
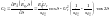
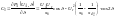В ПОЗИЦИОННОЙ модели режимы электрической системы зависят от положения ротора СГ. Наличие демпфирующих свойств не учитывается. Характеристическое уравнение:

12. Критерии статической устойчивости для сложных ээс. Критерий Гурвица.

Рассмотрим систему N узлов c (N-1) уравнениями.

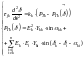
Составляем характеристический определитель (N-1)* (N-1):

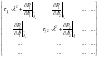
ПОРЯДОК УРАВНЕНИЯ – 2*(N-1)

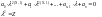
Для того, чтобы исходный режим был статически устойчив, необходимо, чтобы при условии

, все остальные коэффициенты характеристического уравнения были положительны.

Z<0 (вещественный), λ чисто мнимые.

Еще один критерий устойчивости – свободный член характеристического уравнения:

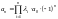
При утяжелении режима нарушение статической устойчивости носит апериодический характер, то есть появляется один положительный вещественный корень, что соответствует изменению знака свободного коэффициента.

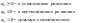
Критерий Гурвица.

позволяет определить статически устойчивый режим или нет или количество корней характеристического уравнения.

ВСЕ ДИАГОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ ДОЛЖНЫ БЫТЬ >0!

Количество смен знаков в определителях соответствует количеству корней с положительной вещественной частью.