17.Транспортная задача линейного программирования.

По терминологии обобщенной модели академика Л.В. Канторовича, двухиндексная задача оптимизации загрузки оборудования соответствует производственной системе с накапливаемыми и потребляемыми ингредиентами. Накапливаемыми ингредиентами являются обрабатываемые заказы, потребляемыми – машинное время используемого оборудования. Общее число ингредиентов равно m + n. Способы функционирования рассматриваемой системы определяются видами продукции, обрабатываемой на раз-личных машинах. Общее число способов функционирования равно m * n.

С позиций математики рассматриваемая задача принадлежит классу распределительных задач линейного программирования. Частным случаем распределительных задач является транспортная задача.

Постановка транспортной задачи

В m пунктах отправления (у поставщиков) сосредоточено a_i, i=1,...,m единиц однородного груза, который следует доставить в n пунктов назначения (потребителям) с потребностями в грузе b_j, j=1,...,n. В базовой (закрытой) модели транспортной задачи предполагается, что суммарные запасы груза в пунктах отправления равны суммарным потребностям в грузе пунктов назначения:

Известны затраты на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения: c_ij, i=1,...,m, j=1,...,n. Необходимо найти план перевозки груза, при котором весь груз будет вывезен из пунктов отправления, в каждый пункт назначения будет доставлено требуемое число единиц груза и при этом общие затраты на перевозку груза будут минимальными.

М атематическая модель транспортной задачи (закрытого типа)

Найти min f =

при условиях

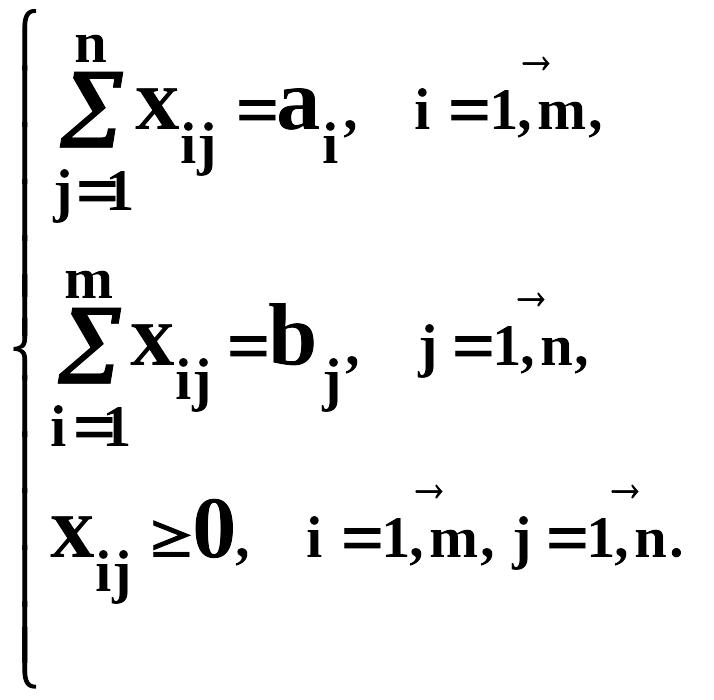
x_ij – число единиц груза, подлежащих перевозке из i -го пункта отправления в j -й пункт назначения;

f – общие затраты на перевозку груза.

18.Задача о назначениях.

Частным случаем транспортной задачи является следующая задача о назначениях. Имеется n должностей и n претендентов на эти должности. Известна полезность каждого претендента при назначении на каждую из должностей, т.е. задана матрица c_ij, i,j=1,...,n. Требуется произвести назначение каждого претендента на одну из должностей, обеспечив при этом максимальную суммарную полезность назначений.

Обозначим через x_ij, i,j=1,...,n неизвестные, которые будут принимать значение, равное единице, если i-й претендент получает назначение на j-ю должность, и нулю - в противном случае; через f обозначим суммарную полезность назначений.

Н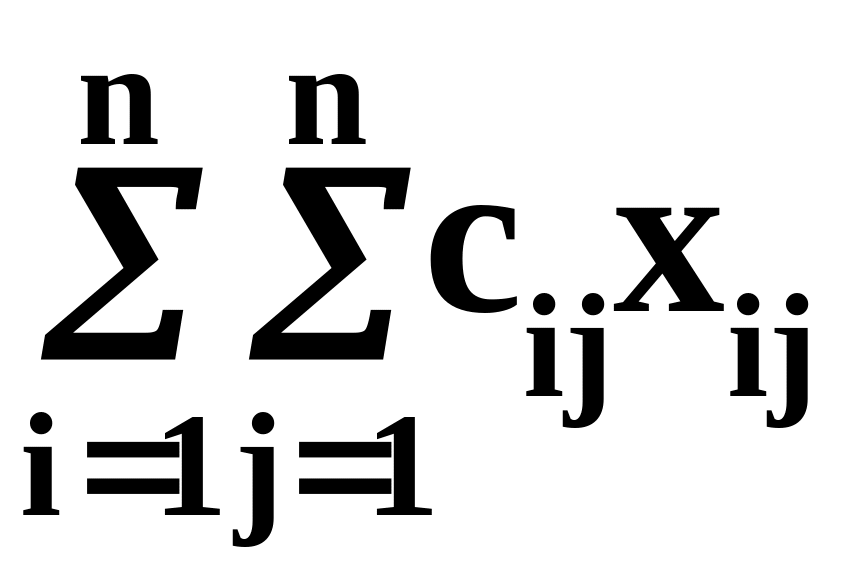 айти max f =

п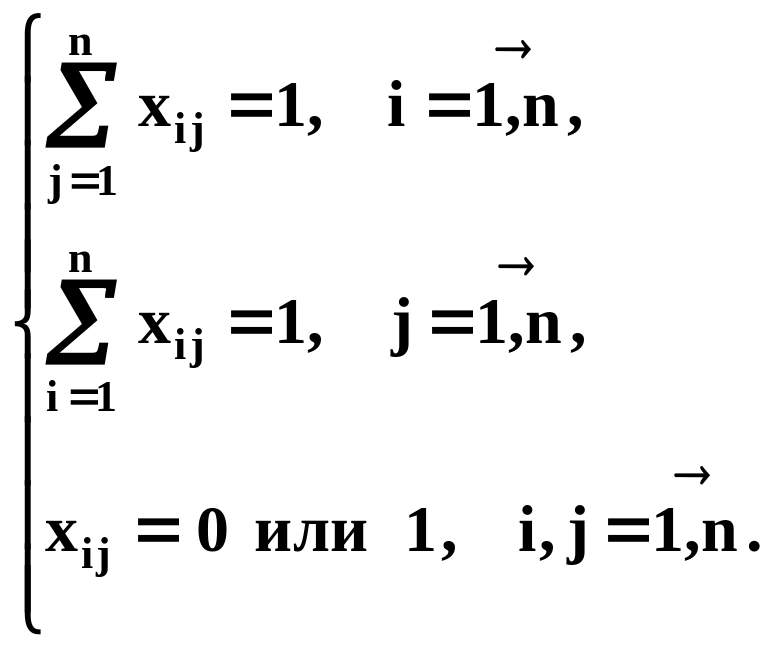 ри условиях

Переменные, которые могут принимать одно из двух значений: 0 или 1, называются булевыми (двоичными) переменными. Задача о назначениях является задачей с булевыми неизвестными - частным случаем задачи целочисленного линейного программирования.

19.Метод динамического программирования. Постановка задачи оптимизации сроков замены производственного оборудования.

Примеры задач нелинейного программирования

К числу задач нелинейного программирования относятся:

• задача оптимизации последовательности обработки заказов (решается методом случайного поиска),

• задача оптимизации сроков замены оборудования (решается методом динамического программирования),

• задача управления запасами (для ее решения применяется классический аппарат поиска экстремума функции нескольких переменных).

На этапе постоптимизационного анализа задач линейного и нелинейного программирования используются методы целочисленного и параметрического программирования. При решении задач в стохастической постановке применяется метод компьютерного моделирования и используются эконометрические модели для обработки результатов моделирования.

Ключевым вопросом долгосрочного планирования является выработка оптимальной политики обновления производственных мощностей предприятия. Особенно актуальна эта задача для полиграфических предприятий в связи с высоким возрастом печатных машин.

Метод динамического программирования

Для научного обоснования оптимальной политики обновления производственного оборудования используется математическая модель задачи о замене оборудования, разработанная американскими математиками Р. Беллманом и С. Дрейфусом [1].

Задача решается методом динамического программирования. Этим методом решаются задачи, которые естественным путем или искусственно расчленяются на ряд шагов или этапов. Оптимальное решение такого рода задач вырабатывается последовательно, поэтапно на основе оптимальных решений семейства взаимосвязанных локальных задач, различающихся по длительности процесса планирования и уровню использования ресурсов. Связь между оптимальными решениями локальных задач задается функциональ-ными уравнениями (рекуррентными соотношениями) Р. Беллмана. Формирование функциональных уравнений – основная трудность в реализации метода динамического программирования.

[1] Р.Беллман, С.Дрейфус. Прикладные задачи динамического программирования. Пер. с англ. М., Наука, 1965. с. 156-166

Рассматривается плановый период продолжительностью N лет. Вследствие физического износа машины имеет место падение с течением времени ее производительности, увеличение эксплуатационных расходов и, в целом, снижение годовой прибыли от функционирования машины.

Научно-технический прогресс в отрасли приводит к моральному старению эксплуатирующейся машины, которое проявляется в том, что ежегодно появляются новые модели (поколения) машины с лучшими технико-экономическими показателями.

Явление физического и морального старения машины учитывается в модели с помощью семейств кривых S(p,t) и C(p,t). Первое из них характеризует зависимость годовой прибыли от возраста и поколения машины, второе – затраты на замену машины.

Для аналитического описания годовой прибыли от эксплуатации машины принята экспоненциальная функция в виде

S(p,t)=P*e^b(p–1)*e^–gt»P*(1+b)^(p–1)/(1+g)^t где t - возраст машин; p - индекс поколения; P - параметр, за-висящий от типа машины и расчетной д.ед.; b - коэффициент, учитывающий темпы морального старения машины; g - коэф-фициент, учитывающий темпы физического старения машины.

Затраты на замену машины существенно зависят от ее возраста и аналитически выражаются функцией

C(p,t)=R/P*e^d(p–1)*e^j*t»R/P*(1+d)^(p–1)*(1+j)^t где R - параметр, зависящий от типа машины; d, j - коэффи-циенты, учитывающие темпы морального и физического старения машины.