13.Двухиндексная задача раскроя материала.

q – число видов исходного материала; n_k, k = 1, ..., q – число возможных вариантов раскроя для k-го вида материала; a_kij, k =1, ..., q, i = 1, ..., m, j = 1, ..., n_k – число заготовок i-го вида, выкраиваемых из одного листа (рулона) k-го вида при применении j-го варианта его раскроя; c_kj, k = 1, ..., q, j = 1, ..., n_k – площадь отхода при раскрое одного листа (рулона) k-го вида по j-му варианту; d_k, k = 1, ..., q – запасы листов (рулонов) k-го вида, которые могут быть использованы для раскроя; x_kj, k = 1, ..., q, j = 1, ..., n_k – листов (рулонов) k-го вида, подлежащих раскрою по j-му варианту; f – суммарная площадь отходов материала.

Н айти min f = при условиях

14.Задача оптимизации загрузки взаимозаменяемого оборудования.

На участке, оснащенном m разнотипными взаимозаменяемыми машинами, планируется обработка n заказов. Известны фонды машинного времени (в часах) для каждой машины a_i, i = 1, …, m; производственные задания (в учетных единицах) по каждому заказу b_j, j = 1, …, n; время, затрачиваемое на обработку одной учетной единицы каждого заказа на каждой машине t_ij, i = 1, …, m, j = 1, …, n. Кроме того, определены удельные затраты, связанные с обработкой заказов на различных машинах c_ij, i = 1, …, m, j = 1, …,n (в д.ед/уч.ед.).

Т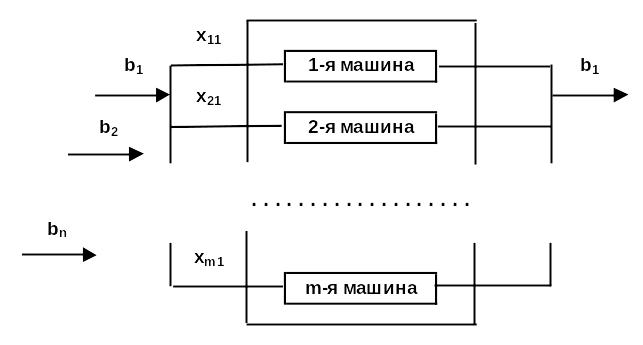 ребуется так распределить заказы на машины, чтобы минимизировать суммарные затраты на выполнение производственных заданий по всем заказам, обеспечив при этом работу каждой машины в пределах располагаемого фонда машинного времени.

С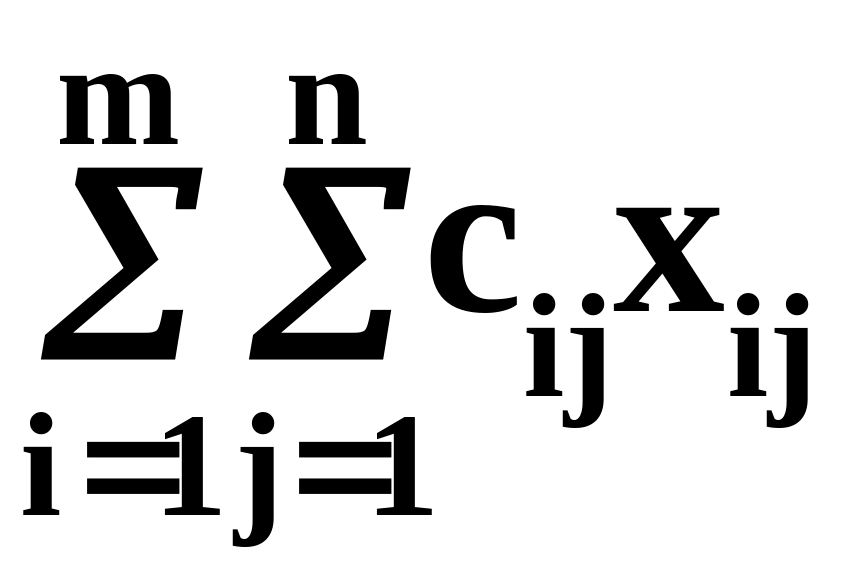 труктурная схема производственной системы с взаимозаменяемым оборудованием

Найти min f =

п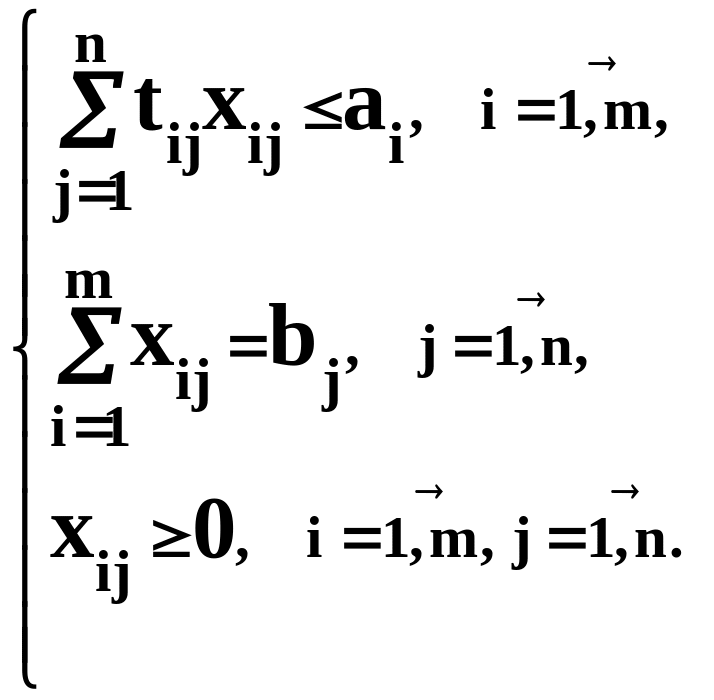 ри условиях

x_ij – число учетных единиц j-го заказа, обрабатываемых на i-й машине;

f –общие затраты на обработку всех заказов.

15. Задача оптимизации загрузки взаимозаменяемого оборудования с булиевыми переменными.

На участке, оснащенном m разнотипными взаимо-заменяемыми машинами, планируется обработка n заказов. Известны фонды машинного времени (в часах) для каждой машины a_i, i = 1, …, m; производственные задания (в учетных единицах) по каждому заказу b_j, j = 1, …, n; время, затрачиваемое на обработку одной учетной единицы каждого заказа на каждой машине t_ij, i = 1, …, m, j = 1, …, n. Кроме того, определены удельные затраты, связанные с обработкой заказов на различных машинах c_ij, i = 1, …, m, j = 1, …,n (в д.ед/уч.ед.).

Т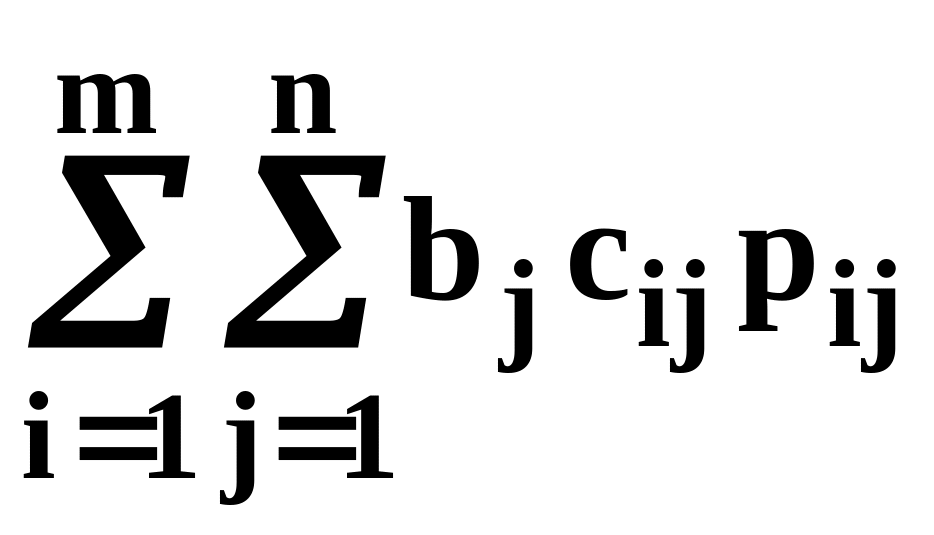 ребуется так распределить заказы на машины, чтобы минимизировать суммарные затраты на выполнение производственных заданий по всем заказам, обеспечив при этом работу каждой машины в пределах располагаемого фонда машинного времени.

Найти min f =

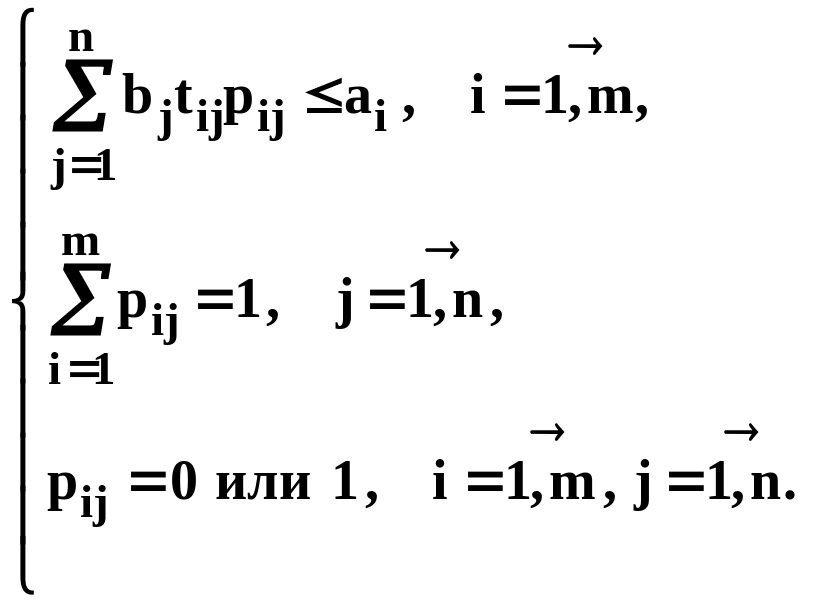
при условиях

Найти min f =

п ри условиях

p_ij равно 1, если j-й заказ распределяется на i-ю машину, и 0 в противном случае.

16.Задача выбора оптимальных технологических маршрутов.

Часто по организационно-технологическим соображениям удобно производить обработку заказов партиями. Каждый заказ может рассматриваться как одна партия изделий либо может делиться на несколько партий.

Каждая партия проходит обработку на одной из машин участка, т.е. используется определенный технологический маршрут для каждой партии изделий. Для каждого заказа (вида продукции) может быть выделено несколько допустимых маршрутов, поэтому возникает задача выбора оптимальных технологических маршрутов и интенсивности их загрузки (оптимальных объемов партий), обеспечивающих минимальные суммарные затраты на выполнение всех заказов в установленных объемах.

n_m – общее число технологических маршрутов;

m – индекс маршрута (m = 1, …, n_m);

M^j, j = 1, …, n – множество индексов маршрутов, связанных с обработкой j-го заказа;

M^ki, k = 1, …, q; i = 1, …, m_k – множество индексов маршрутов, связанных с использованием i-й машины k-го участка;

x_m, m = 1, …, n_m – количество учетных единиц заказа, обрабатываемых с использованием m-го технологического маршрута;

t_kim, k = 1, …, q; i = 1, …, m_k; m = 1, …, n_m – затраты машинного времени i-й машины k-го участка, при обработке одной учетной единицы продукции на m-м технологическом маршруте;

s_m, m = 1, …, n_m – затраты на обработку одной учетной единицы продукции на m-м технологическом маршруте;

z_km, k = 1, …, q; m = 1, …, n_m – затраты на обработку одной учетной единицы продукции на k-м участке для m-го технологического маршрута

Н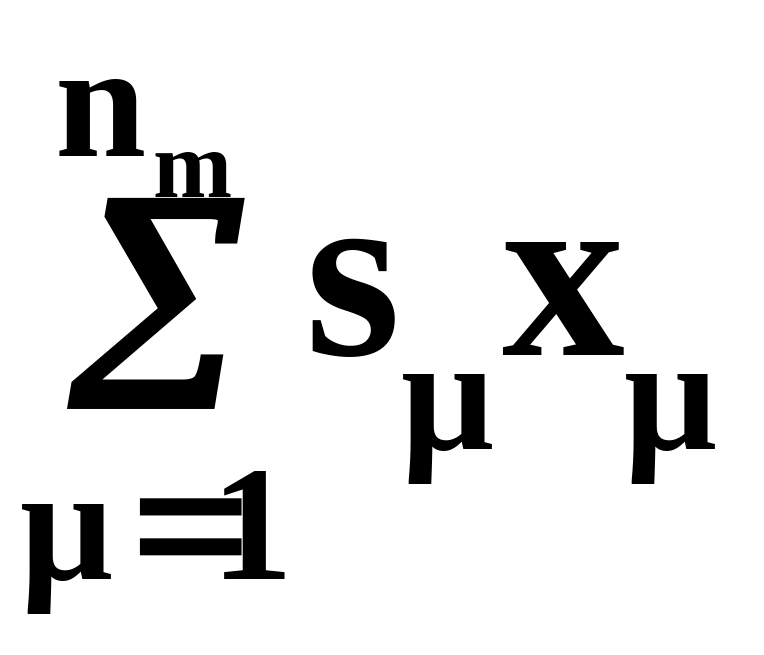 айти min f =

п ри условиях

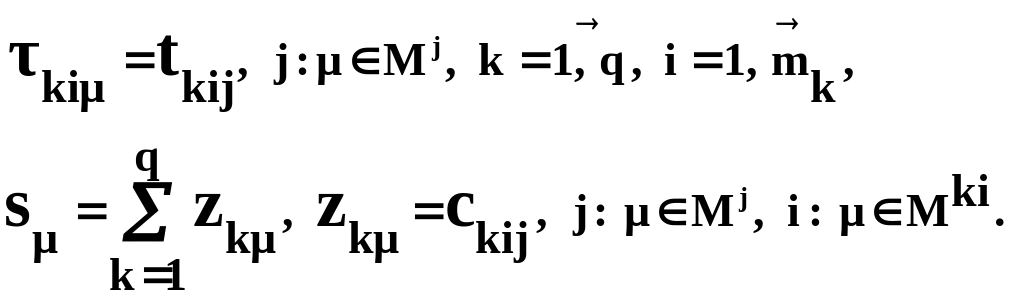
где:

Пример задачи оптимизации технологических маршрутов

Рассчитать оптимальный план загрузки производственного оборудования формного цеха. Цех должен изготовить стереотипы текстовых форм по двум заказам. По первому заказу производственная программа составляет 20 стереотипов (листов набора), по второму – 30 стереотипов. Процесс изготовления стереотипов включает три последовательно выполняемые технологические операции (на трех участках). Первая операция (набор) может выполняться на трех видах взаимозаменяемого оборудования, вторая операция (изготовление оригиналов форм) – на двух видах взаимозаменяемого оборудования, третья операция (получение стереотипов) – на двух видах оборудования.