9 .Математическая модель задачи с расширением спроса.

Найти max f =

п ри условиях

Q – общие затраты на дополнительные ресурсы и расширение спроса; u_j, j=1,...,n – имеющийся объем спроса на продукцию j-го вида, w_j, j=1,...,n – расширение спроса на продукцию j-го вида, q_j, j=1,...,n – затраты на единицу спроса.

Перспективы развития производственной системы определяются на основе параметрирования суммы средств, затрачиваемых на расширение производства.

Эффективный путь развития производства связан с комплексным оптимальным наращиванием запасов ресурсов и расширением спроса на базисные виды продукции.

При расширении производства необходимо учитывать не только цены на дополнительно приобретаемые ресурсы, но и затраты на расширение спроса на отдельные виды продукции.

10.Постановка и математические модели задачи раскроя материала.

О бозначив x_j, j=1,...,n - число листов (рулонов), раскраиваемых по j-му варианту, f – суммарную площадь отходов материала, запишем базовую модель задачи оптимального раскроя материала в виде:

Найти min f =

п ри условиях

Д вухиндексная модель задачи раскроя материала

Н айти min f = при условиях

Модель задачи с комплектным раскроем

Н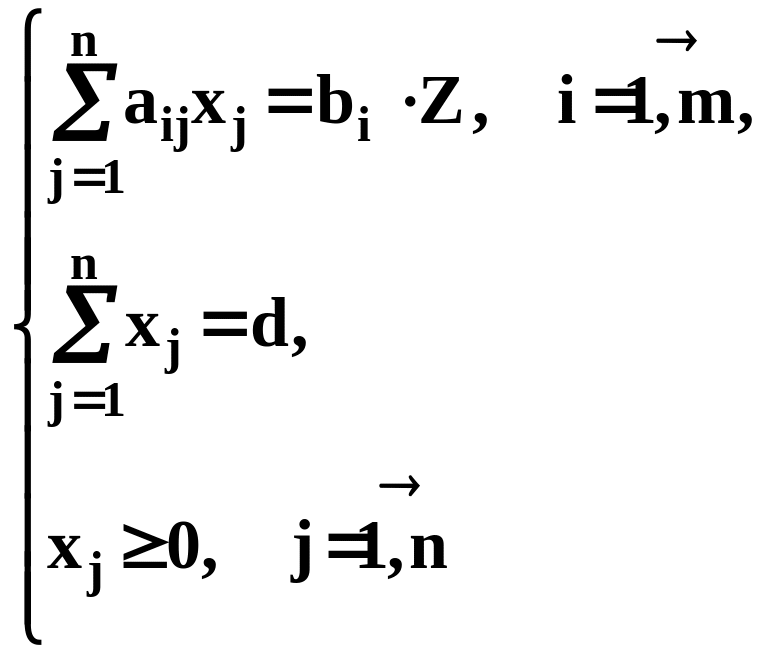 айти max f = Z при условиях

1 1.Двойственная задача для задачи раскроя материала.

Н айти max F = при условиях

y_i, i=1,...,m - неизвестные двойственной задачи (условные показатели технологичности раскроя заготовок); F - суммарная технологичность всей партии раскраиваемых заготовок.

С огласно первой теореме двойственности, общие затраты материала при оптимальном плане раскроя равны суммар-ной технологичности всей партии заготовок:

Условные коэффициенты технологичности характеризуют приращение общих затрат материала на каждую дополни-тельно выкраиваемую заготовку соответствующего вида.

П ризнак оптимальности плана раскроя, вытекающий из 2-й теоремы двойственности: план раскроя оптимален, если для вариантов раскроя, включенных в этот план, ограниче-ния двойственной задачи выполняются в виде равенств:

а для вариантов раскроя, не включенных в план раскроя, ограничения двойственной задачи выполняются в виде неравенств:

12.Применение двойственных оценок для решения задачи раскроя материала.

Первая группа условий образует систему нормальных линейных алгебраических уравнений с m неизвестными и позволяет рассчитать значения двойственных оценок для анализируемого плана раскроя.

Д алее полученные значения двойственных оценок должны использоваться для проверки выполнения второй группы условий. Если не сформировано множество допустимых вариантов раскроя, то невозможно напрямую проверить выполнение второй группы условий. Однако, возможна косвенная проверка на основе решения вспомогательной задачи, имеющей целью найти вариант раскроя материала, оптимальный для значений двойственных оценок, определен-ных из первой группы условий.

Н айти max z = при условиях