7.Стоимостной анализ оптимального решения задач.

Диапазоном устойчивости оптимального плана при измене-нии удельной прибыли c_j называется множество значений c_j, при которых остаются неизменными состав дефицитных ресурсов, номенклатура и оптимальные объемы выпускаемой продукции, а оптимальные значения суммарной прибыли и цен дефицитных ресурсов линейно изменяются при переходе от нижней к верхней границе диапазона устойчивости (в част-ном случае, некоторые из них не изменяются).

Диапазоном устойчивости оптимального плана при измене-нии объема ресурса b_i называется множество значений b_i, при которых остаются неизменными номенклатура выпускаемой продукции, состав и условные цены дефицитных ресурсов, а оптимальные значения суммарной прибыли и объемов выпускаемой продукции линейно изменяются при переходе от нижней к верхней границе диапазона устойчивости (в частном случае, некоторые из них не изменяются).

8 .Постановка, математическая модель и порядок решения целочисленной задачи с пороговыми значениями объемов выпуска продукции.

Н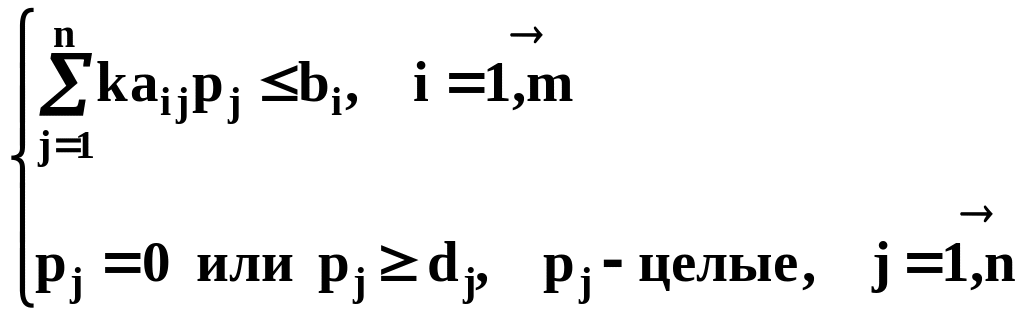 айти max f = при условиях

k – размер партии; p_j, j=1, ..., n – число производимых партий продукции j-го вида (неизвестные); d_j, j=1, ..., n – минимально допустимое число производимых партий продукции j-го вида.

Задача формирования целочисленного плана выпуска продукции с пороговыми значениями объемов выпуска продукции является задачей нелинейного целочисленного программирования и не может быть решена в автоматиче-ском режиме с помощью пакета “Поиск решения” ЭТ Excel.

Для ее решения применяется интерактивный метод ветвей и границ: решение исходной задачи нелинейного целочислен-ного программирования сводится к решению последователь-ности порожденных задач линейного целочисленного программирования, каждая из которых формируется в интерактивном режиме с учетом ограничений, связанных с пороговыми значениями объемов выпуска продукции.

а) Решение целочисленной задачи планирования производства с пороговыми значениями объемов выпуска продукции начинается с определения текущего плана для базовой системы ограничений, включающей условие целочисленности значений неизвестных, но не учитывающей пороговые значения объемов выпуска продукции.

Если получен приемлемый допустимый план, то задача решена. Если получен допустимый план, не являющийся приемлемым, то задача решения не имеет. Наконец, если текущий план для исходной задачи оказался приемлемым, но недопустимым, то реализуется алгоритм целенаправленного перебора текущих планов, связанный с формированием в интерактивном режиме множества порожденных задач и их последовательным решением с помощью пакета “Поиск решения”.

б) Если на некотором шаге в результате решения одной из порожденных задач получен неприемлемый текущий план, то убивается соответствующая ему ветвь иерархической структуры порожденных задач.

Если получен приемлемый, но недопустимый план, в котором положительная компонента p_j меньше порогового значения d_j, то производится дробление очередной задачи на две порожденные задачи: для первой из пары порожденных задач в систему ограничений вводится дополнительное условие p_j = 0 и условие p_j ³ d_j для второй порожденной задачи.

Каждая из порожденных задач является задачей целочисленного линейного программирования и решается с помощью пакета “Поиск решения” после интерактивного уточнения настроек в диалоговом окне пакета.

с) Если на данном шаге впервые получен приемлемый допустимый план, то он запоминается вместе с соответствующей ему величиной суммарной прибыли. Если же ранее уже был найден допустимый план с лучшей величиной суммарной прибыли, то убивается ветвь иерархической структуры порожденных задач, соответствующая вновь найденному допустимому плану. В противном случае запоминается новый допустимый план и убивается ветвь ранее найденного допустимого плана.

Процедура решения исходной задачи заканчивается, когда в иерархической структуре порожденных задач остается единственная ветвь, соответствующая лучшему из найденных допустимых решений.