4.Двойственность в линейном программировании.

Число неизвестных двойственной задачи равно числу основных ограничений исходной задачи и, наоборот.

Матрица основных ограничений двойственной задачи образуется путем транспонирования соответствующей матрицы исходной задачи.

Параметрами ограничений (правыми частями) двойственной задачи служат коэффициенты при неизвестных в целевой функции исходной задачи и, наоборот.

З наки неравенств основных ограничений двойственной задачи противоположны знакам неравенств основных ограничений исходной задачи; если исходная задача - на максимум, то двойственная к ней - на минимум и, наоборот.

Н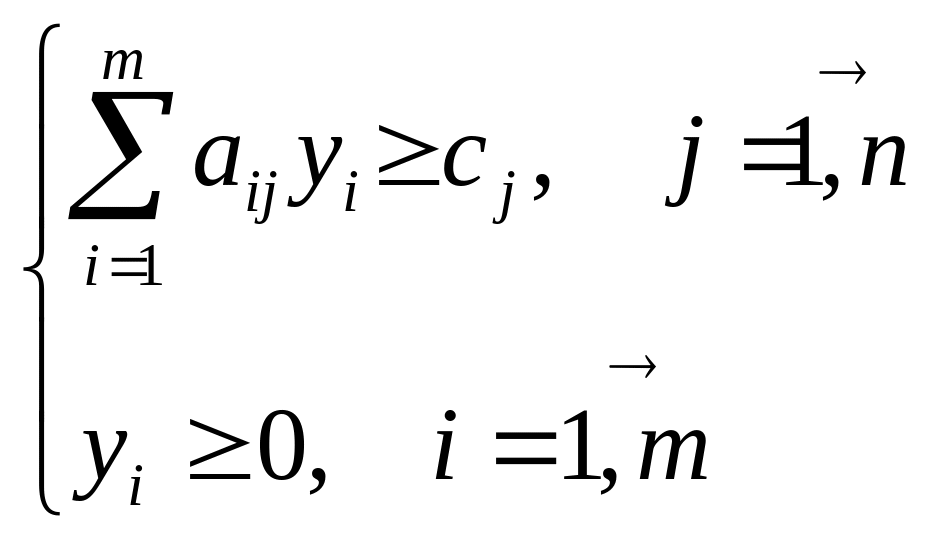 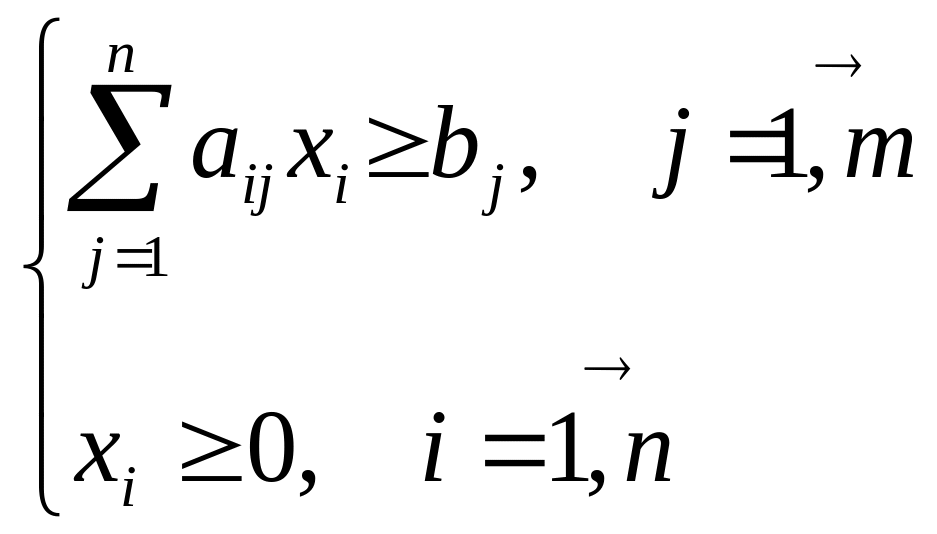айти min z = max f = при условиях

y_i, i=1,...,m - неизвестные двойственной задачи (условные цены ресурсов). Условные цены ресурсов отражают значимость ресурсов в конкретных условиях данной производственной ситуации

5.Теоремы двойственности.

Т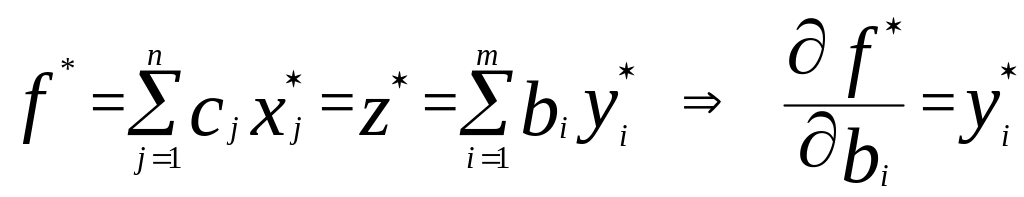 еоремы двойственности устанавливают взаимосвязь между оптимальными решениями прямой и двойственной задач. Согласно первой теореме двойственности суммарная стоимость ресурсов по оптимальным условным ценам равна общей прибыли от реализации всей продукции, изготовленной предприятием при оптимальном плане выпуска продукции из имеющихся запасов ресурсов.

Условные цены ресурсов характеризуют приращение суммарной прибыли на каждую дополнительную единицу запаса соответствующего ресурса.

В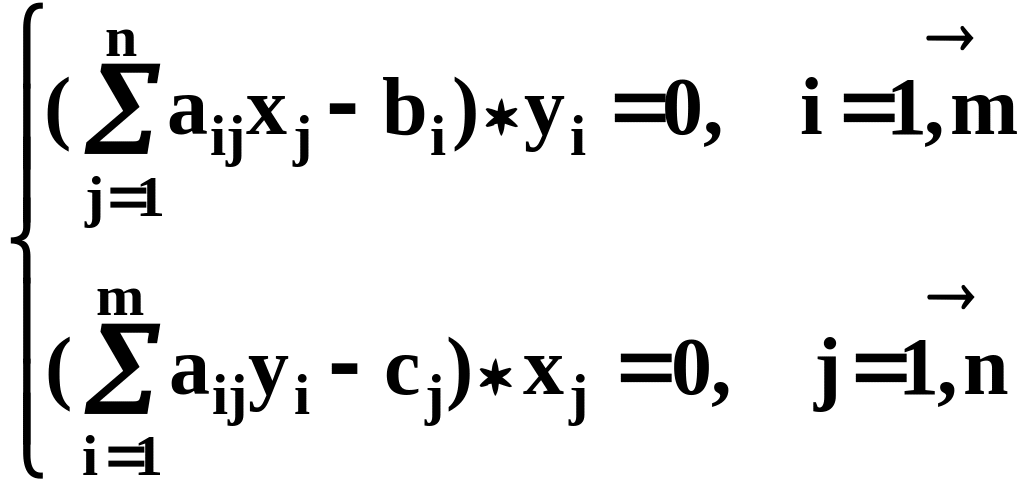 торая теорема двойственности устанавливает соотношения между компонентами оптимальных решений прямой и двойственной задач. Для того, чтобы допустимые решения x₁,x₂,...,x_n; y₁,y₂,...,y_m прямой и двойственной задач были бы их оптимальными решениями, необходимо и достаточно выполнение условий:

Экономическая интерпретация теорем двойственности

Ресурс i-го вида имеет ненулевую цену, если полностью расходуется в процессе производства (такой ресурс будем называть дефицитным). Продукции j-го вида производится, если стоимость затраченных на ее производство ресурсов по условным ценам равна прибыли от реализации данной продукции (такой вид продукции будем называть базисным). Сравнительно небольшие изменения удельной прибыли или запасов ресурсов не приводят к нарушению условий второй теоремы двойственности: оптимальная номенкла-тура выпускаемой продукции и состав дефицитных ресурсов остаются неизменными.

6.Содержание и порядок проведения постоптимизационного оптимального решения задач.

Разработка рекомендаций по заблаговременной организационно-технологической подготовке производства на случай возможных изменений производственной ситуации.

Разработка субоптимального плана, не слишком сильно отличающегося от теоретически оптимального по суммарной прибыли, но более удобного с точки зрения организации производства.

Поиск эффективных путей развития производства и радикального повышения суммарной прибыли.

Разработка предложений по дополнительной (по сравнению с рекомендуемым планом) организационно-технологической подготовке производства проводится на основе:

Анализа возможных неблагоприятных структурных (качественных) изменений производственной ситуации и разработки альтернативных (“аварийных”) планов, минимизирующих потери суммарной прибыли в этих условиях.

Анализа устойчивости оптимального плана при случайных количественных изменениях параметров производственной ситуации, не контролируемых со стороны предприятия (в пределах ± 30% от номинальных значений).

Компьютерного моделирования оптимальных объемов выпуска продукции при случайных изменениях производственной ситуации.