1.Понятие экономико-математической модели производственной системы. Задача и методы.

Экономико-математические методы и модели (ЭММиМ) предназначены для поиска и обоснования путей повышения эффективности производства, рационального использования ресурсов, обеспечения конкурентоспособности предприятий в условиях рыночной экономики. На основе ЭММиМ с помощью современных компьютерных технологий получают данные для анализа эффективности производственных систем, прогнозирования их поведения при возможных изменениях производственной ситуации и выработки управленческих решений для достижения поставленных целей.

Э кономико-математической модель – это формализованное (математическое) описание условий и результатов функционирования производственной системы с позиций экономики. Модель строится с помощью переменных, параметров, множеств, функций, уравнений, неравенств, логических правил.

Н айти max (min) при условиях

г де f, g_i , - заданные, в общем случае нелинейные функции n переменных - b_i – заданные параметры.

З апись означает, что может иметь место неравенство вида , уравнение или неравенство вида . В экономических приложениях функцию f называют целевой функцией. Если f и g_i , - линейные функции, то имеет место задача линейного программирования.

2.Формулировка и математическая модель задачи линейного программирования.

Н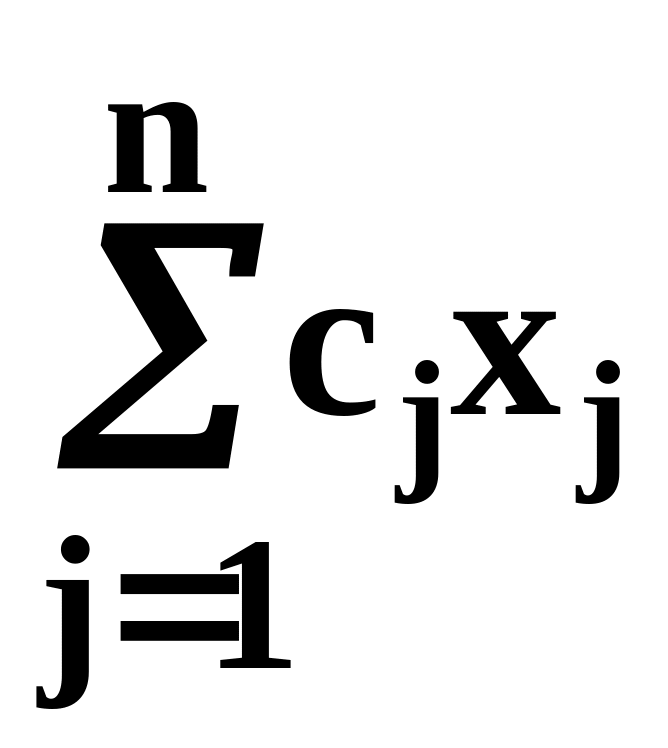 аиболее популярными задачами математического программирования для экономических приложений являются задачи линейного программирования, в которых целевая функция f и функции ограничений являются линейными функциями неизвестных x₁, x₂, …, x_n :

Найти max (min) f =

при условиях

Задачи планирования производства, раскроя материалов, загрузки производственного оборудования и ряд других задач линейного программирования относятся к задачам технико-экономического планирования, для которых академик Канторович Л.В. предложил обобщенную модель и единую методику решения, введя понятия ингредиентов и способов функционирования производственной системы.

Под ингредиентами производственной системы понимаются готовая продукция и услуги, производимые системой (накапливаемые ингредиенты), а также используемые в процессе производства материальные, трудовые, финансовые и др. ресурсы (потребляемые ингредиенты). Под способами функционирования производственной системы понимаются различные варианты использования имеющихся ресурсов для производства продукции и услуг.

3.Постановка и математические модели задачи планирования производства.

Предприятие может производить продукцию n видов, используя m видов ресурсов. Известны: a_ij, i=1,...,m, j=1,...,n - нормы затрат ресурсов i-го вида на производство единицы продукции j-го вида; b_i, i=1...,m - запасы ресурсов i-го вида; c_j, j=1,...,n - прибыль от реализации единицы продукции j-го вида вида.

Требуется найти объемы производства продукции каждого вида x_j, j=1,...,n, при которых будет достигнута максимальная суммарная прибыль f при условии сбалансированности плана производства продукции по каждому виду ресурсов.

Б азовая модель задачи планирования производства

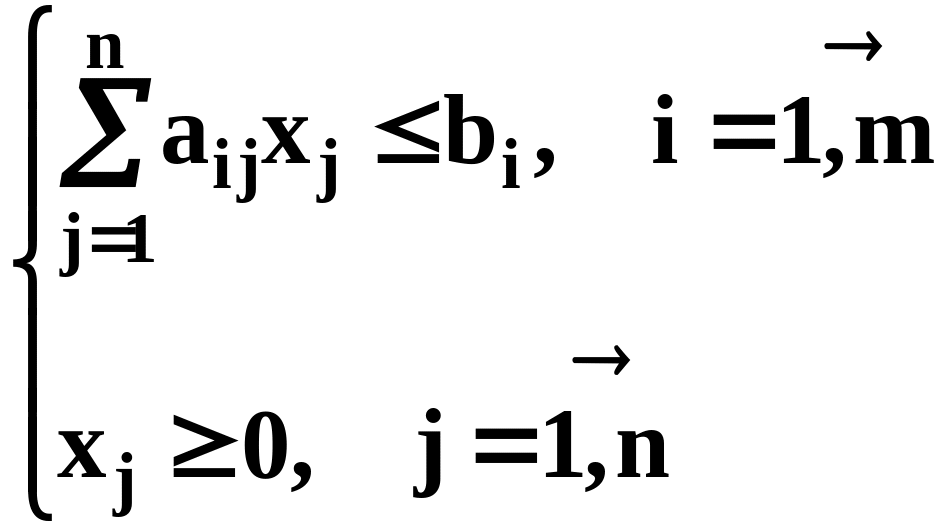Н айти max f = при условиях

М одифицированная модель задачи планирования производства

Н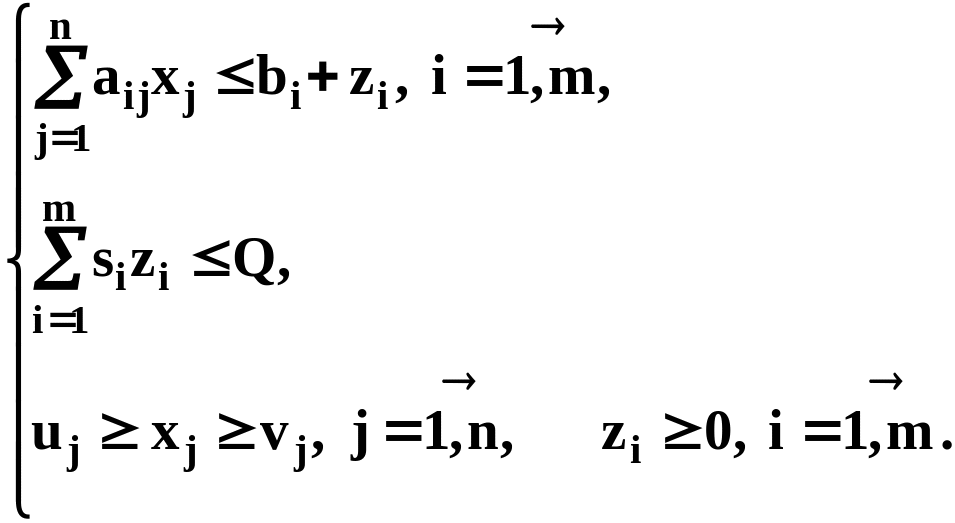 айти max f = при условиях

Q – сумма на приобретение дополнительных ресурсов; s_i, i=1,...,m – стоимость единицы i-го ресурса; z_i, i=1,...,m – число приобретаемых единиц i-го ресурса; u_j, j=1,...,n – объем спроса, v_j, j=1,...,n – объем заказа на продукцию j-го вида.

Д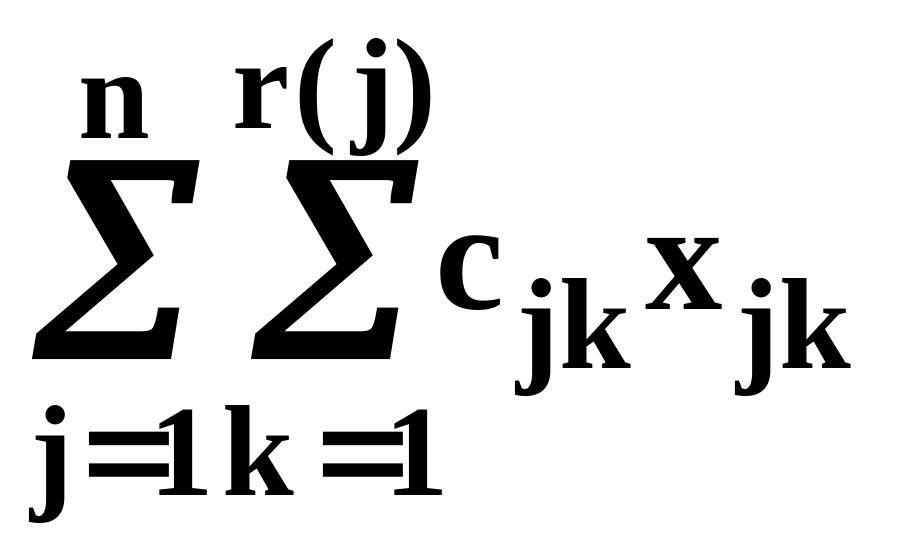 вухиндексная модель задачи планирования производства

Найти max f =

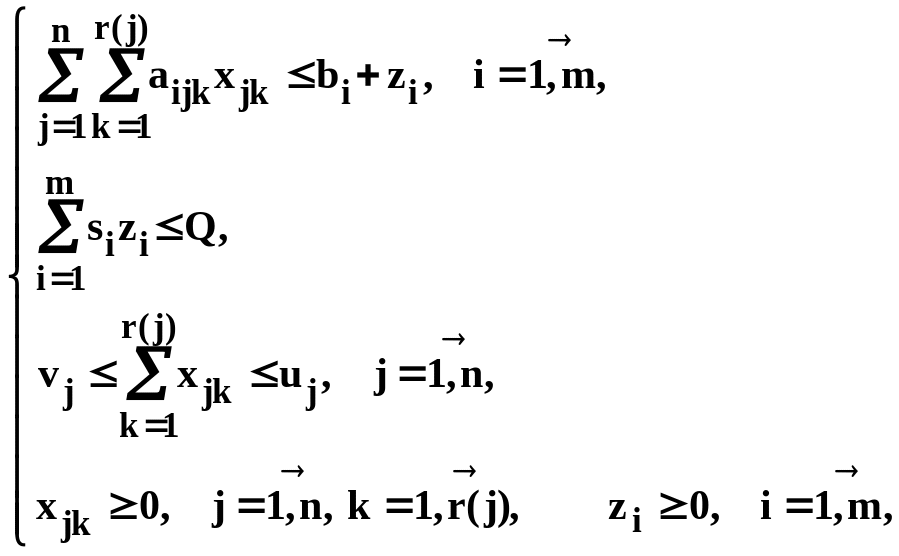при условиях

r(j) j=1, ..., n - число возможных технологических вариантов изготовления продукции j-го вида;

c_jk, j=1, ..., n, k=1, ..., r(j) - прибыль от реализации единицы продукции j-го вида, изготовленной по k-му технологиче-скому варианту;

a_ijk, i=1, ..., m, j=1, ..., n, k=1, ..., r(j) - норма расхода ресурса

i-го вида на производство единицы продукции j-го вида при применении k-го технологического варианта;

x_jk, j=1, ..., n, k=1, ..., r(j) - планируемый объем выпуска продукции j-го вида с использованием k-го технологиче-ского варианта.