4.Нормальный закон распределения и его значение для прикладной статистики.

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности.

Нормальный закон распределения также называется законом Гаусса

распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

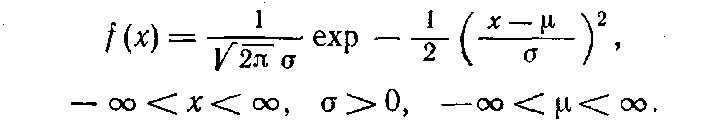
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистике. Физическая величина, подверженная влиянию значительного числа независимых факторов, могущих вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Свойства

Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиями и соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией .

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Центральная предельная теорема

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

отклонение при стрельбе, погрешности измерений, рост живых организмов

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).

Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием центральной предельной теоремы.

5. Статистические гипотезы в задачах регрессии.

Статистической гипотезой Н называется предположение относительно параметров или вида распределения случайной величины Х.

Статистическая гипотеза Н называется простой, если она однозначно определяет распределение случайной величины Х; в противном случае, гипотеза Н называется сложной.

Проверяемая гипотеза называется нулевой гипотезой и обозначается Но. Это гипотеза об отсутствии различий, называется нулевой потому, что содержит число 0: X1- Х2=0, где X1, X2 - сопоставляемые значения признаков.

Альтернативная гипотеза - это гипотеза о значимости различий. Она обозначается как H1. Альтернативная гипотеза - это то, что мы хотим доказать, поэтому иногда ее называют экспериментальной гипотезой.

Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными.

Направленные гипотезы: H0: X1 не превышает Х2, H1: X1 превышает Х2,

Ненаправленные гипотезы: H0: X1 не отличается от Х2 Н1: Х1 отличается от Х2

Правило, по которому принимается решение принять или отклонить нулевую гипотезу, называется критерием.

Статистический критерий - это решающее правило, обеспечиваю­щее надежное поведение, то есть принятие истинной и отклонение ложной гипотезы с высокой вероятностью.

В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна-Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила.

Мощность критерия - это его способность выявлять различия, если они есть, тое есть это его способность отклонить нулевую гипотезу об отсутствии различий, если она неверна.

Ошибка, состоящая в том, что мы приняли нулевую гипотезу, в то время как она неверна, называется ошибкой II рода. Вероятность такой ошибки обозначается как β. Мощность критерия - это его способность не допустить ошибку II рода, поэтому мощность равна 1 — β. Мощность критерия определяется эмпирическим путем. Одни и те же задачи могут быть решены с помощью разных критериев, при этом обнаруживается, что некоторые критерии позволяют выявить различия там, где другие оказываются неспособными это сделать, или выявляют более высокий уровень значимости различий. Возникает вопрос: а зачем же тогда использовать менее мощные критерии? Дело в том, что основанием для выбора критерия может быть не только мощность, но и другие его характеристики, а именно: а) простота;

б) более широкий диапазон использования; в) применимость по отношению к неравным по объему выборкам; г) большая информативность результатов.

Уровень значимости - это вероятность того, что мы сочли различия существенными, а они на самом деле случайны.

Когда мы указываем, что различия достоверны на 5%-ом уровне значимости, или при р<0,05, то мы имеем виду, что вероятность того, что они все-таки недостоверны, составляет 0,05. Когда мы указываем, что различия достоверны на 1%-ом уровне значимости, или при р<0,01, то мы имеем в виду, что вероятность того, что они все-таки недостоверны, составляет 0,01.

Уровень статистической значимости - это вероятность отклонения нулевой гипотезы, в то время как она верна.

Ошибка, состоящая в том, что мы отклонили нулевую гипотезу, в то время как она верна, называется ошибкой I рода. Вероятность такой ошибки обозначается как α. Если вероятность ошибки - это α, то вероятность правильного решения: 1 - α. Чем меньше α, тем больше вероятность правильного решения.

Правило отклонения H0 и принятия H1:

Если эмпирическое значение критерия равняется критическому значению, соответствующему р<0,05 или превышает его, то H0 отклоняется, но мы еще не можем определенно принять H1. Если эмпирическое значение критерия равняется критическому значению, соответствующему р<0,01 или превышает его, то H0 отклоняется и принимается H1.

Исключения: критерий знаков G, критерий Т Вилкоксона и критерий U Манна Уитни. Для них устанавливаются обратные соотношения.

Таким образом, формулирование гипотез систематизирует предположения исследователя и представляет их в четком и сжатом виде. Благодаря гипотезам исследователь не теряет ориентира в процессе расчетов и ему легко понять после их окончания, что, собственно, он обнаружил. Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, - достоверными.

Проверка гипотез осуществляется с помощью критериев статистической оценки различий. При описании каждого критерия в руководстве даны формулировки гипотез, которые он помогает нам проверить.

Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X₁,X₂,...,X_p. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных), а не причинно-следственные отношения.

Цель регрессионного анализа: 1.Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)2.Предсказание значения зависимой переменной с помощью независимой(-ых)3. Определение вклада отдельных независимых переменных в вариацию зависимой.

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.