4. Смеси распределений

Пусть имеется набор функций распределения

Пусть далее - неотрицательные числа, .

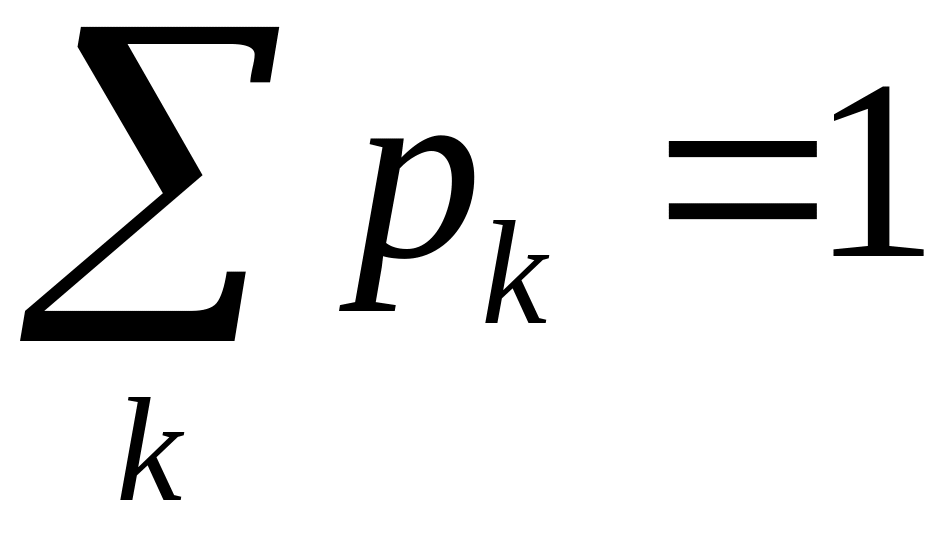Определим функцию

Функция обладает всеми свойствами функции распределения (это можно доказать, для конечного набора функций распределения доказательство очевидно).

Определение.

Функция распределения называется дискретной смесью распределений с весами В частности, если p_i=0 при i>k, то смесь называется конечной.

Пример.

Пусть  – с.в., принимающая значения 1,2,…,k с вероятностями и пусть имеется набор с.в. , определенных на вероятностном пространстве и имеющих функции распределения Будем считать, что любые события (=i) и (A), где AF – независимы.

Тогда с.в. имеет функцию распределения, задаваемую формулой .

Действительно, по формуле полной вероятности имеем:

.

Пример:

В ящике 1000 деталей, характеризующихся параметром  - случайной величиной. 700 деталей изготовлены на заводе 1, 300 – на заводе 2. В силу различной технологии распределения с.в.  представляются функциями .

Из ящика наудачу извлекается деталь. Функция распределения параметра  для этой детали имеет вид

Справедлива следующая теорема.

Теорема:

Пусть F(x) – произвольная функция распределения. Тогда существует функция дискретного распределения F₁(x), функция непрерывного распределения F₂(x) и функция сингулярного распределения F₃(x), а также неотрицательные постоянные 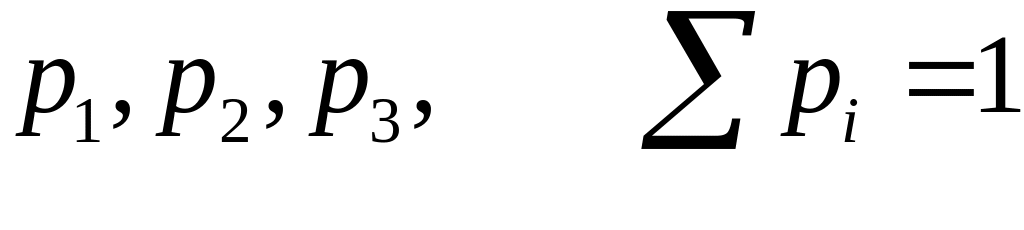такие, что

.

Дискретные, непрерывные и сингулярные распределения называются чистыми, а все остальные – смешанными распределениями.

Пример 1.

Пусть имеется элемент со случайным временем  безотказной работы. Причем  -

экспоненциальная (показательная) с.в. с параметром ;

Найти вероятность отказа элемента в интервале времени при условии, что элемент проработал до времени x.

Решение

Т.О. случайное время безотказной работы при условии, что элемент проработал до времени x, также есть экспоненциальная с.в.

Т.О. распределение времени остатка безотказной работы не зависит от того, сколько времени элемент уже проработал.

Рассмотрим

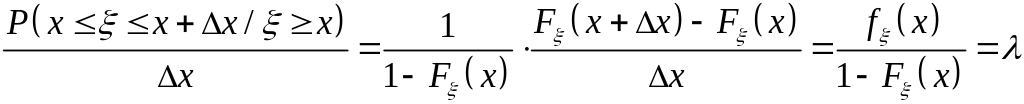
Т.О.  можно интерпретировать как «интенсивность отказа».

Пример 2.

Пусть  - с.в. – время жизни некоторого лица.

1. Пусть вероятность того, что некоторое лицо умрет в течение времени равна

2. Будем считать, что смерть или выживание данного лица в промежуток времени не зависит от того, что было до момента времени t₁.

3. Вероятность смерти в момент рождения равна 0.

Найти функцию распределения .

Решение.

- вероятность смерти до возраста t.

Обозначим – вероятность дожить до возраста t.

.

- вероятность не умереть в течение времени .

По условиям 2,3 эта вероятность не зависит от того, что было до времени t и

.

Т.О.

и удовлетворяет дифференциальному уравнению

и

- вероятность смерти до возраста t.

22