1. Борелевская –алгебра. Измеримые функции.
2. Функция распределения и ее основные свойства.
3. Виды случайных величин (дискретные непрерывные, сингулярные).
4. Смеси распределений
1. Борелевская –алгебра. Измеримые функции.
Цель этой лекции – определить метод для отображения произвольного вероятностного пространства на множество действительных чисел. Это полезно, так как с множеством действительных чисел работать легче, чем с произвольным вероятностным пространством.
Итак, роль нового
вероятностного пространства
будет играть R
– множество действительных чисел.
Определим на нем –алгебру,
содержащую множества
.
Напомним, что –алгебра
есть класс множеств, замкнутый относительно
счетного числа операций дополнения,
объединения и пересечения.
Введенная –алгебра
называется Борелевской и обозначается
.
Класс борелевских множеств достаточно
широк, он содержит множества вида
(дополнение к
),
множества
(пересечение множеств
и
),
отдельные точки (пересечение бесконечного
числа интервалов
),
множества вида
,
.
Фактически все, встречающиеся на практике
множества являются борелевскими.
Пусть теперь нам
задано вероятностное пространство
,
а также (R,B)
– вещественная прямая с борелевской
–алгеброй
на ней. Рассмотрим некоторое отображение
g
пространства
на вещественную прямую R.
Отображение g
ставит в соответствии каждому
действительное число
;
.
Определение.
Для данной функции g
и множества
будем называть прообразом
множества А,
обозначаемым
,
множество тех
для которых
:
.
Определение. Будем называть функцию g() измеримой, если прообразом каждого борелевского множества является множество, принадлежащее –алгебре F.
Определение.
Пусть задано вероятностное пространство
.
Случайной
величиной
на этом пространстве называется измеримая
функция, принимающая значения на
вещественной оси;
.
Мы ограничиваем наше рассмотрение только измеримыми функциями, чтобы в прообразы борелевских множеств не попали множества, не принадлежащие –алгебре событий, и значит, которые могут не иметь меры, то есть вероятности. Как проверить, является ли функция измеримой или нет?
Критерий измеримости. Функция является измеримой, если прообразом любого множества , а – произвольное число, является множество принадлежащие –алгебре событий F.
Осталось рассмотреть,
как отображаются вероятности событий
из
в
.
Рассмотрим
борелевское множество A,
соответствующее лучу
.
Его прообразом, относительно отображения
является множество А0
из –алгебре
событий F.
Вероятностью для случайной величины
принять значение из интервала
будем считать вероятность события А0,
то есть
.
Так как значение
x
можно брать на оси R
произвольно, то
есть функция от x,
определенная на всей числовой оси.
Определение.
Пусть
– с.в., определенная на неком вероятностном
пространстве. Функция
называется функцией распределения
с.в..
Основные свойства функции распределения.
1.
определена при всех
.
2.
(то есть
- неубывающая).
3.
(по свойствам вероятности).
4.-5.
.
Пусть
- две монотонные последовательности,
.
Пусть событие An
равносильно попаданию с.в.
в интервал
.
Очевидно, что
.
Так как
,
то по условию непрерывности
[ Пусть
- возрастающая последовательность
событий
и
,
тогда
при
]
.
Т.О.
,
что
.
Если
,
то тем более
, а так же
.
Отсюда вытекает свойства 4-5.
6. Функция
-
непрерывна слева, то есть
.
Пусть
- любая возрастающая последовательность,
сходящаяся к x.
.
По аксиоме сложения вероятностей
Ряд в правой части
состоит из неотрицательных чисел и
сходится к
,
поэтому
, что
Т.О.
,
кроме того
,
поэтому
.
В силу произвольности
имеем
.
Замечание:
Справедлива теорема о том, что любая
функция
,
удовлетворяющая свойствам 1-6, является
функцией распределения некоторой с.в.,
то есть можно построить вер. пространство
и ввести на нем с.в., функция распределения
которой совпадет с
.
Это означает, что функция распределения может рассматриваться без исходного вероятностного пространства, что часто и делают. Функция распределения – исчерпывающая характеристика с.в.
Дополнительные свойства функции распределения.
7.
,
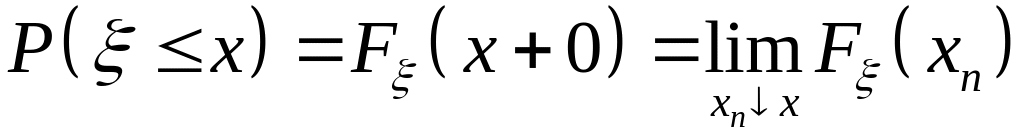где
– любая убывающая последовательность,
сходящаяся к x.
По аксиоме сложения вероятностей
.
8.
.
