Вопрос 1.

Суть способа Лежандра заключается в том, чтобы зная исходную сторону по формулам плоской тригонометрии вычислить остальные стороны.

Рассмотрим этот способ.

Из сферической тригонометрии известно, что сумма безошибочно известных углов сферического треугольника равна (180 ̊+ε), где ε – сферический избыток.

Приведём формулы вычисления ε

=

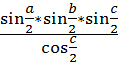
где соответствие величины представлено на чертеже

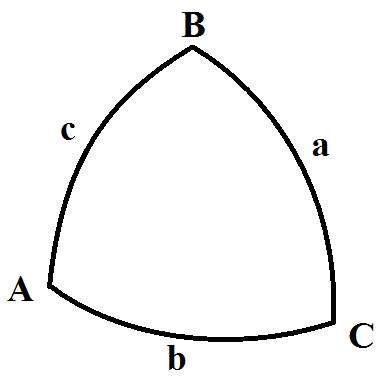
Углы А,В,С – измерены

a, b, c – длины сторон, выраженные в угловой мере.

Решение треугольников на сфере осуществляется по формуле

= =

если известно, то

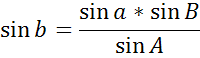
радиус шара в данной точке, можно определить значение дуги в линейной мере.

Rb=S_b

Раньше, когда вычисления осуществлялись по таблицам, использовались формулы плоской геометрии. Для этого из каждого угла, измеренного на эллипсоиде, вычиталась величина равная 1/3 сферического избытка.

Если задана исходная сторона S_a и исправленные за сферический избыток углы

A’=A-

B’=B-

C’= C-

=

S_b=

В заключении покажем вывод формулы сферического избытка

= *

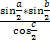Поскольку сферический избыток- малая величина, его можно заменить величиной

*

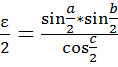Вопрос 2.

Способ аддиментов

Аддимент от слова “qaddition” – добавлять.

В этом случае ввод поправок в углы, как в способе Лежандра, а в стороны решение выполняется по способу плоского прямоугольника.

в качестве исходной формулы запишем формулу вычисления сторон на сфере:

Пусть у нас имеется измеренная сторона S_a, тогда:

С тем чтобы получить решение по правилам плоской тригонометрии, синусы сторон разлагают в ряд Тейлора, ограничиваясь первыми членами разложения.

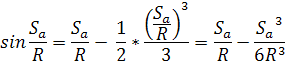
Считая, что на расстоянии 100 м, ряд Тейлора можно не рассчитывать.

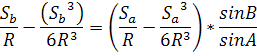
Можно считать, что приведенные члены в третьей степени являются какими-то поправками.

МОДУЛЬ 3

Решение главных геодезических задач на эллипсоиде

1. Общие сведения о главной геодезической задаче на поверхности эллипсоида

2. Пути и методы решения главной геодезической задачи

3. Точность решения главной геодезической задачи

4. Вывод формул путём разложения в ряд разности широт, долгот и азимутов

5. Решение обратной геодезической задачи со средними аргументами

6. Способ Бесселя для решения главной геодезической задачи

7. Требования к решению главной геодезической задачи на любые расстояния

Вопрос 1.

В геодезии на плоскости существуют 2 главные геодезические задачи: прямая и обратная.

В прямой геодезической задаче даны координаты X, Y первой точки, дирекционный угол направления с точки 1 на точку 2 (α_1-2). Необходимо определить координаты второй точки.

В обратной геодезической задаче по координатам конечных точек отрезка или прямой линии, необходимо вычислить ее длину S и дирекционный угол α.

На эллипсоиде в сферической геодезии также рассматриваются 2 главные геодезические задачи.

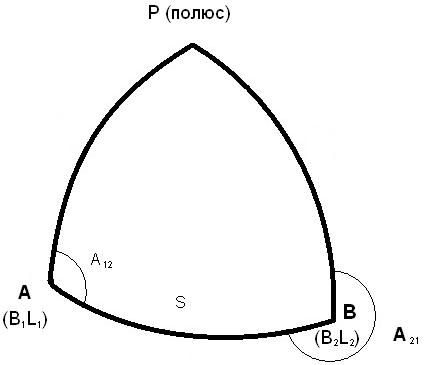
Прямая геодезическая задача: даны B₁, L₁ (широта и долгота точки), длина геодезической линииS, азимут линии в точке А (А₁₂). Необходимо определить B₂, L₂, а также обратный азимут А₂₁.

Обратная геодезическая задача на сфероиде: Даны B₁, L₁, B₂, L₂. Найти длину геодезической линии S, а также азимуты А₁₂ и А₂₁