МОДУЛЬ 2

Геометрия земного эллипсоида

1. Земной эллипсоид. Методы определения его параметров

2. Исходные геодезические данные

3. Система координат на поверхности земного эллипсоида

4. Линейный элемент поверхности

5. Дифференциалы и длины дуг меридианов и параллелей

6. Площадь сферической трапеции

7. Уравнение геодезической линии на поверхности эллипсоида

Вопрос 1.

Поскольку земной эллипсоид является поверхностью относимости, на которой решаются задачи по определению координат точек и с которого точки и линии проецируются на плоскость, то необходимо определить параметры земного эллипсоида.

Земной эллипсоид образуется вращением эллипса вокруг его малой оси. Другими словами эллипсоид называют сфероидом.

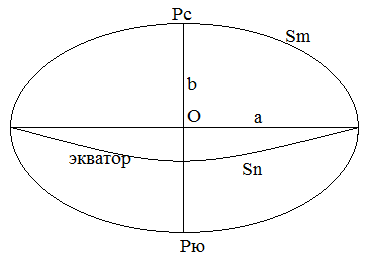
Эллипсоид определяется двумя параметрами. Параметрами земного эллипсоида могут быть:

1. а, в – большая, малая полуось;

2. а, α= , сжатие

3. а, ℓ=

4. ℓ'=

Для решения всех геодезических задач необходимо подобрать такие параметры, при которых эллипсоид наилучшим образом описывает фигуру реальной земли.

Существуют следующие методы определения параметров

1. геометрический

2. физический

Геометрический заключается в измерении дуг меридианов и параллелей, из сравнения этих измерений можно определить параметры. Такой метод называется методом дуг.

Вторым геометрическим методом является метод площадей. Он заключается в определении астрономических координат пунктов геодезической сети, расположенных на большой территории. Далее задаются приближенными параметрами земного эллипсоида а⁰, α⁰. По этим параметрам определяем геодезические координаты пунктов этой сети В⁰, L⁰. В результате обработки этих данных надо получить поправку в эллипсоид δа, поправку сжатия δα и поправки в координаты в координаты δВ, δL. Поправок в координаты пунктов будет столько, каким является двойное число пунктов. Чтобы упростить и решить корректно задачу поправки δB_i и δL_i выражают через поправки в исходный пункт δB₁,δL₁ и δ_А1 – азимут на исходном пункте. В результате у нас будет пять неизвестных δB₁,δL₁ и δ_А, δа, δα.

Физический метод заключается в измерении силы тяжести на пунктах геодезической сети. По расхождениям значений силы тяжести можно также определить параметры земного эллипсоида. Например, сила тяжести на полюсе и экваторе различается между собой. Очевидно, что по разностям таких измерений можно определить сжатие.

Геометрический метод развивается дополнением GPS измерений. На больших расстояниях (600 и более км.) измеряется приращение координат между пунктами, их тоже можно использовать для определения параметров земного эллипсоида.

Вопрос 2.

Под исходными геодезическими датами понимают значение:

1. двух параметров земного эллипсоида;

2. координат исходного пункта на эллипсоиде, а именно геодезической широты, геодезической долготы и азимута, которые астрономическим координатам. Таким образом, названные астрономические координаты определяют ориентировку эллипсоида в центре земли.

Вопрос 3.

Раздел геодезии, в котором решаются задачи на поверхности земного эллипсоида называется сфероидической геодезией.

Все задачи необходимо решать в определённой системе координат.

Различают системы координат:

1)Прямоугольная геоцентрическая система.

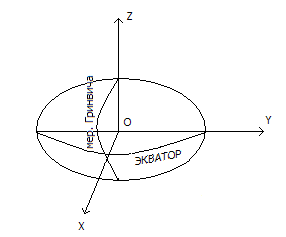
В ней ось X направлена в пересечение экватора и меридиана Гринвича. Ось Z совпадает с осью вращения земли. Начало в центре масс земли. Ось y дополняет систему до правой.

2)Прямоугольная топоцентрическая.

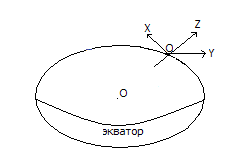
Ось Z направлена в зенит по нормали, ось X на север, ось Y дополняет систему до правой на восток.

3)Геодезическая.

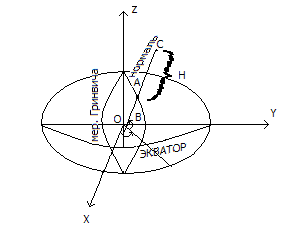
Положение точки А к геодезическим сетям определяется геодезической широтой В, долготой L, геодезической высотой V. В – угол между нормалью и плоскостью экватора.

4)Геоцентрическая угловая.

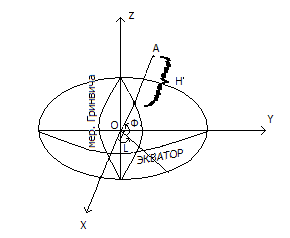
Положение точки А определяется Ф – геоцентрической широтой, L – геодезической долготой, высотой H по радиус-вектору, направленному с центра эллипсоида.

5)СК с приведенной широтой.

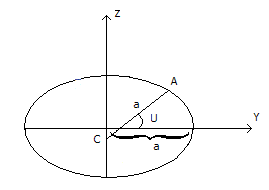
Если через точку А провести радиус-вектор длиной а, точку О чтобы он касался оси вращения в точке С, то угол между этим радиус-вектором и плоскостью СА называется приведенной широтой (U). Долгота остаётся прежней.

6)Прямоугольных сфероидических координат.

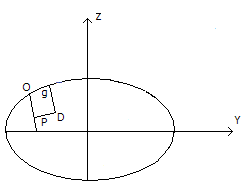
Одной из осей системы является меридианом, а второй кривая линия перпендикулярная меридиану в точке О. Положение точки Д будет определяться криволинейными координатами p и q.

7)Плоские прямоугольные координаты.

Примером является система геодезических координат.

Связь между системами координат:

1)Связь между геодезической широтой и геоцентрическими координатами x и y.

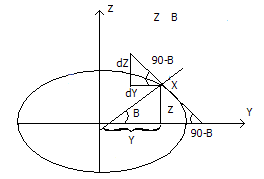
tg(90⁰-B)=

2)Связь между геодезической широтой и геоцентрической широтой.

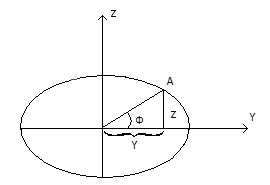
tg Ф= . Исходя из формулы tg(90⁰-B)= и уравнения эллипса меридианного сечения ( )²+( )²=1

Найдём зависимость между L и Ф. Найдём дифференциал эллипса

+ =0

=-

=-

=- *

сtg (90-B)=- tgФ

3)Связь между приведенной широтой и геодезической широтой.

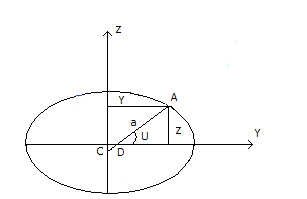
Чтобы установить эту связь найдём чему равен отрезок АД.

z=AD*sinU

y=AC*sin(90-U)

y=a*cosU

Подставим эти значения в уравнения эллипса

(y²/a²)+(z²/b²)=1

(a²*cos²U/a²)+(AD²*sin²U/b²)=1

AD=b

С помощью b можно установить зависимость между геодезической широтой и приведенной.

tg(90⁰-B)=

Для получения dz и dy выразим z и y через приведенную широту.

z=b*sinU

y=a*cosU

dz=b*cosUdU

dy=-asinUdU

tg(90⁰-B)= -

tg(90⁰-B)= - = - ctgU

Данная зависимость является базовой в сфероидической геодезии при вычислении длин дуг и координат точек, так зная приведенную широту и геодезическую долготу легко вычисляются прямоугольные геоцентрические координаты.

Очевидно, что y=r*sinL и x=r*cosL . Для вычисления z воспользуемся отрезком AD. AD=b и z=b*sinU. Для упрощения изложения меридиана в точке А расположен в плоскости чертежа.

r =a*cosU,x=a*cosU*cosL,y=a*cosU*sinL,z=b*sinU – базовые формулы вычисления геоцентрических прямоугольных координат по геодезическим.