4. Какие методы применяются для расчета круглых пластин, нагруженных симметрично.

Пластиной называют плоское тело, ограниченное двумя, по­верхностями, расстояние между которыми мало по сравнению с размерами самих поверхностей. Срединная поверхность пла­стины, т. е. поверхность, равноудаленная от наружных поверх­ностей, представляет собой плоскость. Этим пластины отличаются от оболочек, у которых срединная поверхность не плоская.

Восполь­зуемся методом, предложенным С. Н. Соколовым, который является вариантом метода начальных параметров,

Пластину, подвергаемую сложному нагружению, разделяют на участки, границы между последними выбирают в тех точках, где приложены силы и моменты или где начинается распределенная нагрузка. Когда последняя изменяется скачкообразно, ее представляют в виде суммы двух нагрузок, действующих до наружного края пластины.

Произвольные постоянные интегрирования по участкам сво­дят к начальным параметрам, количество которых не превышает трех. В качестве этих параметров принимают прогиб ω и изгиба­ющие моменты М_r и M_t в центре сплошной пластины или на внутреннем контуре кольцевой пластины.

Для облегчения нахождения постоянных интегрирования ис­пользуют метод выравнивания произвольных постоянных интег­рирования по участкам.

Пример

Исходные данные:

Материал пластины Ст50

Допускаемые напряжения [σ] = 190 МПа

Радиус внутреннего контура пластины r₀ = 30 мм

Радиус внешнего контура пластины R = 110 мм

Средний радиус пластины R_ср = 70 мм

Толщина пластины s = 4 мм

С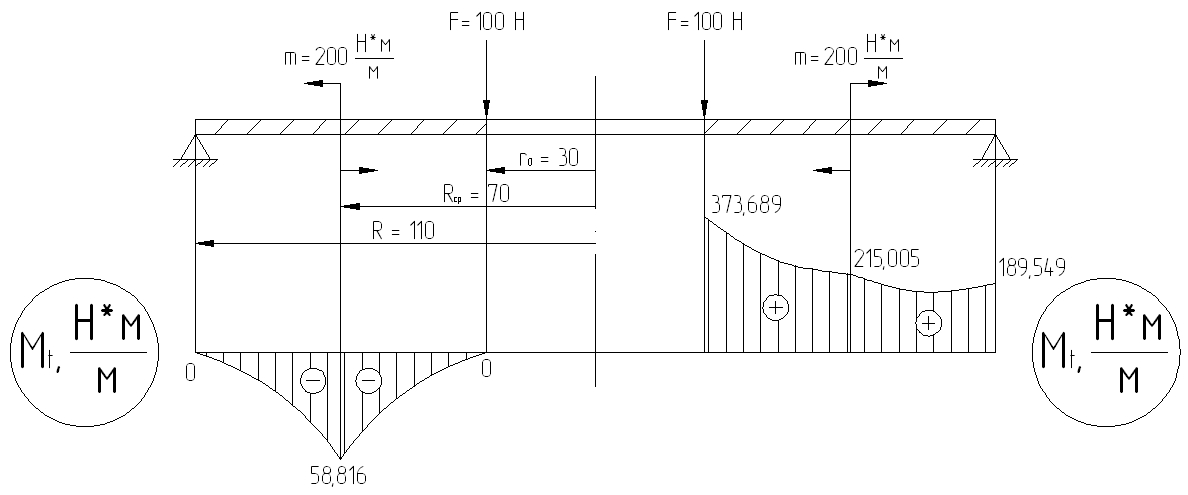 илы, равномерно распределенные по соосным круговым контурам F = 100 Н

Моменты, равномерно распределенные по соосным круговым контурам m = 200

Расчеты:

1. Определяем моменты в радиальном направлении (M_r).

При r = r₀

ψ_rr: λ = r₀/r₀ = 1 => ψ_rr = 1

ψ_rt: λ = r₀/r₀ = 1 => ψ_rt = 0

ψ_rp: λ = r₀/r₀ = 1 => ψ_rp = 0

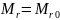
Из граничного условия: при r = r₀ M_r = 0 =>

При r = R

ψ_rr: λ = r₀/R = 0,27 => ψ_rr = 0,5367

ψ_rt: λ = r₀/R = 0,27 => ψ_rt = 0,4633

ψ_rm: λ = R_ср/R = 0,64 => ψ_rm = 0,7848

ψ_rp: λ = r₀/R = 0,27 => ψ_rp = 0,1617

Из граничного условия: при r = R M_r = 0 =>

При r = R_ср

ψ_rr: λ = r₀/R_ср = 0,43 => ψ_rr = 0,5927

ψ_rt: λ = r₀/R_ср = 0,43 => ψ_rt = 0,4073

ψ_rm: λ = R_ср/R_ср = 1 => ψ_rm = 1

ψ_rp: λ = r₀/R_ср = 0,43 => ψ_rp = 0,1102

2. Определяем моменты в окружном направлении (M_t).

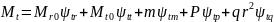
При r = r₀

ψ_tr: λ = r₀/r₀ = 1 => ψ_tr = 0

ψ_tt: λ = r₀/r₀ = 1 => ψ_tt = 1

ψ_tp: λ = r₀/r₀ = 0,43 => ψ_tp = 0

При r = R_ср

ψ_tr: λ = r₀/R_ср = 0,43 => ψ_tr = 0,4073

ψ_tt: λ = r₀/R_ср = 0,43 => ψ_tt = 0,5927

ψ_tp: λ = r₀/R_ср = 0,43 => ψ_tp = 0,0648

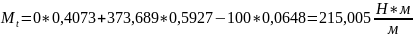
При r = R

ψ_tr: λ = r₀/R = 0,27 => ψ_tr = 0,4633

ψ_tt: λ = r₀/R = 0,27 => ψ_tt = 0,5367

ψ_tp: λ = r₀/R = 0,27 => ψ_tp = 0,1101

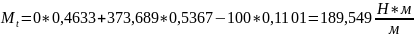
3. Определяем толщину кольцевой пластины.

M_tmax = 373,689

Используем гипотезу наибольших касательных напряжений

=> s = 4 ≥ [s] = 3,44 мм

5. Как применяется метод начальных параметров к расчету пластинок, подвергаемых изгибу или растяжению?

Круглые пластины, нагруженные распределенными симметрич­ными нагрузками, действующими в плоскостях, параллельных срединной плоскости, испытывают растяжение или сжатие.