Манило (метода)

Рис. 3.4. Распределение значений Cq РНК А в группах

Поскольку разница эффективностей систем детекции для РНК А и Б мала и уровни РНК А не меняются в экспериментальных группах, то РНК А можно использовать в качестве референсной РНК для нормировки измеренных уровней РНК Б.

3.4.3.Поиск выбросов с помощью выявления образцов

ссильно отклоняющимися уровнями референсной РНК

Поскольку РНК А удовлетворяет условиям референсной РНК, то по отношению к ней образцы можно рассматривать как технические репликаты, и поэтому значения РНК А можно использовать для поиска выбросов. Причиной появления выбросов может быть, например, присутствие в некоторых образцах ингибиторов ПЦР.

Проведем анализ выбросов для двух выборок – g e n e A _ d o и g e n e A _ p o s . Построим диаграмму размахов значений Cq для каждой выборки (рис. 3.5):

62

Рис. 3.5. Распределение значений Cq РНК А в группах до и после экспериментального воздействия

Из графика видно, что группа g e n e A _ p o s имеет один потенциальный выброс, которым является образец, имеющий максимальное значение Cq. Определим объем выборки g e n e A _ p o s :

> l e n g t h ( g e n e A _ p o s )

[1] 25

Получим значение критерия Граббса для потенциального выброса. В расчетах используются стандартные математические функции – максимальное значение m a x ( ) , математическое ожидание m e a n ( ) , стандартное отклонение s d ( ) :

> ( m a x ( g e n e A _ p o s ) - m e a n ( g e n e A _ p o s ) ) / s d ( g e n e A _ p o s )

[1] 4.624

Рассчитанное значение 4.624 больше, чем 2.822 – критическое значение критерия Граббса для 25 измерений, поэтому отклоняющийся образец признаем выбросом.

63

Определим индекс образца, содержащего ингибиторы реакции амплификации, и исключим его из дальнейшего анализа:

> w h i c h ( g e n e A _ p o s = = b $ o u t )

[ 1 ] 1 0

>g e n e A _ p o s [ 1 0 ] = N A

>g e n e B _ p o s [ 1 0 ] = N A

3.4.4.Проверка условий нормальности распределения данных

иоднородности дисперсий

Убедиться в нормальности распределения данных можно с помощью критерия Шапиро–Уилка. В R данный тест реализуется с помощью функции s h a p i r o . t e s t ( ) . Указав в аргументах данной функции переменную, содержащую некоторую выборку данных, можно легко получить р-значение проверяемой гипотезы. Например, для переменной g e n e A :

Проверка однородности дисперсий между парой групп с помощью критерия Фишера реализуется в R с помощью функции v a r . t e s t ( ) :

> v a r . t e s t ( g e n e B _ d o , g e n e B _ p o s ) $ p . v a l u e

[1] 0.112

Для проверки однородности дисперсий между тремя группами одновременно с помощьюкритерияБартлетта используем функцию bartlett.test():

> b a r t l e t t . t e s t ( g e n e B _ d o ~ g r o u p , e x p ) $ p . v a l u e

[ 1 ] 0 . 4 4 7

3.5.Изучение экспериментальных данных

3.5.1.Изучение различий в абсолютных уровнях исследуемой РНК до и после воздействия

Подготовка данных. В эксперименте перед проведением ПЦР в реальном времени была выполнена нормировка на общую РНК, поскольку в каждой реакции обратной транскрипции использовали ее одинаковое количество. Для решения рассматриваемой в данном разделе задачи дополнитель-

64

ная нормировка производиться не будет. Уровни РНК Б до и после воздействия измеряли у одних и тех же животных, поэтому данные связаны. Так как данные связаны и в первой выборке для 3-го и 4-го образцов, а во второй выборке для 10-го образца значения не определены или удалены (образцы имеют значение NA), то и парные с ними значения необходимо заменить на NA:

> g e n e B _ d o [ 1 0 ] = N A > g e n e B _ p o s [ 3 ] = N A > g e n e B _ p o s [ 4 ] = N A

Проверка гипотезы о равенстве средних значений в выборках. Для этого применим статистический критерий. В аргументах функции параметрического критерия Стьюдента t . t e s t ( ) помимо сравниваемых групп данных необходимо указать:

– информацию о том, связаны данные или нет: p a i r e d = { T R U E или

F A L S E } ;

– вид альтернативной гипотезы: a l t e r n a t i v e = { " t w o . s i d e d " или

" l e s s " или " g r e a t e r " } ;

– информацию об однородности дисперсий: v a r . e q u a l = { T R U E

или F A L S E } .

В аргументах функции непараметрического критерия Манна–Уитни или Вилкоксона w i l c o x . t e s t ( ) помимо сравниваемых групп данных необходимо указать:

– информацию о том, связаны данные или нет: p a i r e d = { T R U E , т. е. рассчитывается критерий Вилкоксона или F A L S E , при этом рассчитывается критерий Манна–Уитни};

– вид альтернативной гипотезы: a l t e r n a t i v e = { " t w o . s i d e d " или

"l e s s " или " g r e a t e r " } .

Врассматриваемом примере данные связаны, условие нормальности не нарушается и дисперсии равны, поэтому используем парный двухсторонний критерий Стьюдента для связанных образцов без поправки на неравенство дисперсий:

> t . t e s t ( g e n e B _ d o , g e n e B _ p o s , p a i r e d = T R U E , a l t e r n a - t i v e = " t w o . s i d e d " , v a r . e q u a l = T R U E ) $ p . v a l u e

[ 1 ] 0 . 0 0 0 5 0 4

Поскольку p-значение меньше 0.05, то гипотеза о равенстве средних значений отвергается.

65

Расчет индивидуальных абсолютных значений РНК Б в экспери-

ментальных образцах. Для расчета абсолютных значений воспользуемся построенной ранее моделью линейной регрессии:

> A Q _ d o = 1 0 ^ ( ( g e n e B _ d o - c o e f ( m B ) [ [ 1 ] ] ) / c o e f ( m B ) [ [ 2 ] ] ) > A Q _ p o s = 1 0 ^ ( ( g e n e B _ p o s -

c o e f ( m B ) [ [ 1 ] ] ) / c o e f ( m B ) [ [ 2 ] ] )

Рис. 3.6. Абсолютные значения уровней РНК Б в экспериментальных образцах

до и после экспериментального воздействия

Представим результаты расчетов на графике (рис. 3.6):

> A Q = c b i n d ( A Q _ d o , A Q _ p o s )

> p l o t ( A Q [ 1 , ] , y l i m = c ( 5 0 0 0 0 , 2 0 0 0 0 0 0 ) , x l i m =

p a r ( n e w = T R U E )

p l o t ( A Q [ i , ] , y l i m = c ( 5 0 0 0 0 , 2 0 0 0 0 0 0 ) , x l i m = c ( 0 . 5 , 2 . 5 ) , p c h = 1 9 , l o g = " y " , y l a b = " " , x l a b = " " , x a x t = " n " ,

y a x t = " n " , m a i n = " " ) l i n e s ( A Q [ i , ] ) }

66

> t e x t ( x = 1 . 5 , y = 1 5 0 0 0 0 0 , l a b e l s = " p = 0 . 0 0 0 5 " , f o n t = 3 )

>l a = a s . v e c t o r ( c ( " До воздействия" , " После воздействия" ) )

>a x i s ( 1 , a t = s e q ( 1 , 2 , b y = 1 ) , l a b e l s = l a , f o n t = 1 )

3.5.2.Изучение различий в относительных уровнях исследуемой РНК

вразных возрастных группах

Проверка гипотезы о равенстве средних значений в трех возрастных группах. Перед применением статистического критерия выполним нормировку индивидуальных значений Cq РНК Б для каждого образца с использованием значений Cq референсной РНК, как это описано в работе Митчелла и соавторов [12]. Для этого рассчитаем нормированные значения следующим образом: CqРНК_Б норм = CqРНК_Б – (CqРНК_А – CqРНК_А медиана), где

CqРНК_Б – Cq РНК Б рассматриваемого образца, CqРНК_А – Cq РНК А этого

же образца, CqРНК_А медиана – медиана Cq РНК А всех образцов. Нормированные значения CqРНК_Б норм запишем в переменную geneB_do_norm:

> g e n e B _ d o _ n o r m < - c ( 3 2 . 6 8 , 3 0 . 2 7 , N A , N A , 2 9 . 6 9 ,

3 1 . 7 1 , 3 2 . 3 5 , 3 0 . 7 4 , 3 1 . 0 4 , 3 0 . 0 7 , 3 0 . 0 7 , 3 0 . 9 7 , 3 0 . 5 7 , 2 8 . 8 9 , 2 9 . 5 8 , 3 0 . 8 4 , 2 9 . 8 2 , 3 0 . 0 2 , 2 9 . 2 8 , 2 8 . 7 1 , 2 8 . 1 9 , 2 8 . 2 4 , 2 8 . 6 9 , 2 8 . 6 0 , 2 7 . 4 3 )

Поскольку данные в выборках не связаны, используем парный двухсторонний критерий Стьюдента для несвязанных образцов без поправки на неравенство дисперсий, так как условие нормальности не нарушается и дисперсии равны. Применим критерий Стьюдента для попарного сравнения групп. Чтобы учесть множественные сравнения необходимо в аргументе функции указать p.adjust.method = {bonferroni или BH или BY} для применения попра-

вок Бонферрони, Беньямини–Хохберга или Беньямини–Йекутили соответственно. В данном случае будет произведено три парных сравнения, поэтому используем поправку Бонферрони. Получим матрицу р-значений:

67

Результаты расчета показывают, что р-значение при сравнении групп 1 и 2 больше 0.05, поэтому гипотеза о равенстве средних значений принимается. При сравнении двух оставшихся пар групп р-значение меньше 0.05, поэтому для них гипотезы о равенстве средних значений отвергаются.

Расчет средних относительных количеств РНК Б в трех возрастных группах. Выполним расчет средних относительных количеств РНК Б с по-

мощью метода 2(– Cq) [13]. Определим переменные:

>r e f = g e n e A _ d o # значения C q референсной РНК

>t a r = g e n e B _ d o # значения C q исследуемой РНК

Найдем разницу между Cq исследуемой и референсной РНК для каждого образца и таким образом выполним нормировку:

> d c q = t a r – r e f ; d c q

Усредним по группам нормированные значения:

> m e a n s . d c q = t a p p l y ( d c q , g r o u p , m e a n , n a . r m = T ) ; m e a n s . d c q

Найдем групповые стандартные отклонения:

> s d = t a p p l y ( d c q , g r o u p , s d , n a . r m = T ) ; s d

Примем за единицу среднее количество РНК Б в группе 1 и вычислим относительные количестваРНК Б в группах 2 и 3. Для этого сначала рассчитаем Cq:

> d d c q = m e a n s . d c q – m e a n s . d c q [ 1 ]

а затем относительные количества

> r q = 2 ^ - d d c q ; r q

Загрузим и установим в R дополнительные пакеты, необходимые для использования функций b a r p l o t 2 ( ) и p l o t C I ():

>i n s t a l l . p a c k a g e s ( " g p l o t s " )

>l i b r a r y ( g p l o t s )

Представим результаты расчетов графически четырьмя разными способами. На рис. 3.7, а представлена точечная диаграмма, где точки соответствуют средним значениям, а «усы» – стандартному отклонению:

> p a r ( m f r o w = c ( 1 , 4 ) )

68

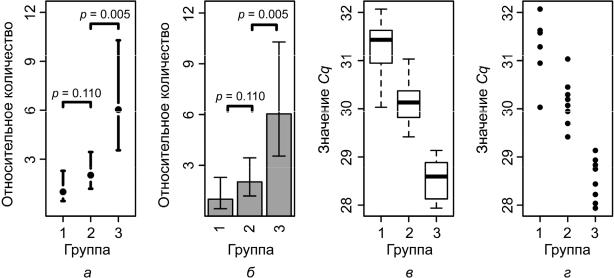
> p l o t C I ( x = c ( 1 : 3 ) , y = r q , u i w = ( 2 ^ - ( d d c q - s d ) ) - 2 ^ -

d d c q , l i w = ( 2 ^ - d d c q ) - 2 ^ - ( d d c q + s d ) , x l i m = c ( 0 . 7 , 3 . 3 ) ,

Укажем на графике названия групп:

> l a = a s . v e c t o r ( c ( " 1 " , " 2 " , " 3 " ) )

> a x i s ( 1 , a t = s e q ( 1 , 3 , b y = 1 ) , l a b e l s = l a , f o n t = 1 )

Укажем на графике р-значения для соответствующих пар групп: > l i n e s ( c ( 1 , 1 , 2 , 2 ) , c ( 4 . 7 , 5 , 5 , 4 . 7 ) , l w d = 2 )

На рис. 3.7, б те же данные средних относительных количеств представлены в виде столбчатой диаграммы:

> b a r p l o t 2 ( 2 ^ - d d c q , p l o t . c i = T R U E , c i . l = 2 ^ - ( d d c q + s d ) , c i . u = 2 ^ - ( d d c q - s d ) , n a m e s . a r g = c ( " 1 " , " 2 " , " 3 " ) , y l a b = " Относительное количество" , x l a b = " Группа" , c o l = " g r e y " , l a s = 2 , c e x . a x i s = 0 . 7 , y l i m = c ( 0 , 1 5 ) , m a i n = " " )

Рис. 3.7. Способы представления результатов расчетов:

а– точечная диаграмма; б – столбчатая диаграмма; в – боксплот;

г– диаграмма рассеяния с указанием значений Cq в индивидуальных образцах

Укажем на графике р-значения для соответствующих пар групп:

> l i n e s ( c ( 1 , 1 , 2 , 2 ) , c ( 4 . 7 , 5 , 5 , 4 . 7 ) , l w d = 2 )

> t e x t ( x = 1 . 5 , y = 5 . 8 , l a b e l s = " p = 0 . 1 1 0 4 " , f o n t = 3 )

69

> l i n e s ( c ( 2 , 2 , 3 , 3 ) , c ( 1 1 . 7 , 1 2 , 1 2 , 1 1 . 7 ) , l w d = 2 )

> t e x t ( x = 2 . 5 , y = 1 2 . 8 , l a b e l s = " p = 0 . 0 0 4 7 " , f o n t = 3 )

На рис. 3.7, в боксплоты иллюстрируют распределения нормированных значений Cq по группам:

> b o x p l o t ( g e n e B _ d o ~ g r o u p , n a m e s = c ( " 1 " , " 2 " , " 3 " ) , x l a b = " Группа" , y l a b = " Значение C q " , m a i n = " " )

На рис. 3.7, г нормированные значения Cq в индивидуальных образцах представлены в виде диаграммы рассеяния:

x l i m = c ( 0 . 6 , 3 . 4 ) , p c h = 1 9 , c e x = 1 , m a i n = " " )

3.5.3.Изучение связи между уровнем исследуемой РНК

ивозрастом животных

Проанализируем связь между уровнем РНК Б до применения воздействия и возрастом животных из групп 1 и 2. В качестве оценки уровня РНК Б будем использовать рассчитанные ранее абсолютные значения. Отберем значения, соответствующие животным из групп 1 и 2:

>a g e 1 2 = a g e [ 1 : 1 6 ]

>A Q _ d o 1 2 = A Q _ d o [ 1 : 1 6 ]

Поскольку значения РНК Б для 3-го и 4-го образцов не определены, то и парные им значения возраста необходимо заменить на NA:

> a g e 1 2 [ 3 ] = N A ; a g e 1 2 [ 4 ] = N A

Вычисляем логарифм абсолютных значений уровней РНК Б: > l A Q _ d o 1 2 = l o g 2 ( A Q _ d o 1 2 )

Применим корреляционный анализ, чтобы количественно оценить силу связи двух параметров и значимость полученной оценки. Рассчитаем коэффициент корреляции Пирсонаи его фактическийуровеньзначимости (р-значение):

> c o r . t e s t ( a g e 1 2 , l A Q _ d o 1 2 , m e t h o d = " p e a r s o n " ) p - v a l u e = 0 . 0 0 0 7

c o r 0 . 7 9

Отобразим результаты анализа на графике (рис. 3.8):

70