
Манило (метода)
.pdfряющим условиям их использования, увеличивается вероятность появления ошибки первого рода. Именно поэтому, если условия нормальности распределения и однородности дисперсий соблюдаются, то рекомендуется использовать параметрические критерии, но если хотя бы одно из этих условий не выполняется, то необходимо воспользоваться непараметрическими критериями.
1.2. Предварительный анализ результатов эксперимента
1.2.1. Анализ грубых ошибок измерения
Если известно, что исследуемый параметр распределен по нормальному закону и имеется достаточное число измерений (более 30), то рекомендуется выявить и исключить из дальнейшего рассмотрения грубые ошибки измерения, которые называют выбросами. Включение выбросов в последующую обработку и анализ данных может вызвать ошибочную интерпретацию результатов анализа. При малом количестве наблюдений (менее 30) поиск и исключение выбросов недопустим, так как в этом случае отклоняющиеся значения могут отражать реально существующий разброс измеряемого параметра. Кроме того, от анализа выбросов лучше отказаться, если распределение исследуемого параметра отлично от нормального. Удаление крайних значений в такой выборке может привести к потере части информации.
На начальном этапе для анализа отклоняющихся значений в имеющейся выборке данных можно построить диаграмму размахов (боксплот) и визуально оценить наличие потенциальных выбросов. Для этого анализируемые значения располагаются в порядке возрастания (упорядоченный ряд). Значения, разделяющие упорядоченный ряд на четыре диапазона, в каждый из которых попадает одинаковое количество значений (25 %), называют квартили. Причем элементы выборки, совпадающие с квартилями, принадлежат обоим диапазонам разделения.
Диаграмма размахов представляет собой «ящик» с «усами» (рис. 1.2). «Ящик» ограничен слева и справа первым (Q1) и третьим (Q3 ) квартилями соответственно. Второй квартиль (Q2 ) соответствует медиане и на диаграм-
ме обозначается линией или точкой внутри «ящика». Границы боксплота обозначают крайние значения выборки, еще попадающие в допустимый диа-
пазон Q3 1.5 Q3 Q1 , Q1 1.5 Q3 Q1 . Значения, которые выходят за пределы допустимого диапазона, изображаются отдельно и рассматриваются как потенциальные выбросы. На рис. 1.2 минимальное значение выборки
11
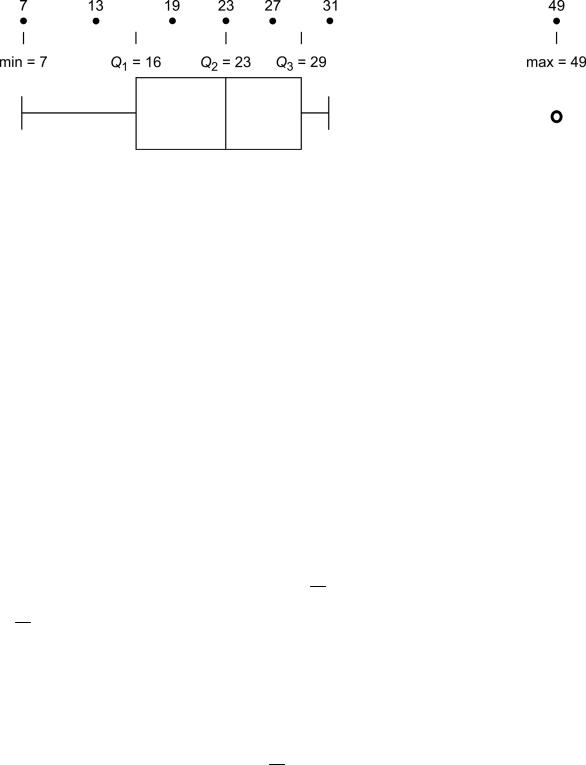
(min) попадает в допустимый диапазон и поэтому соответствует левой границе боксплота, максимальное значение выборки (max) выходит за пределы допустимого диапазона и поэтому обозначено отдельным кружком.
Рис. 1.2. Принцип построения диаграммы размахов
Если на боксплоте отсутствуют потенциальные выбросы, то можно сделать заключение, что выбросов среди измеренных значений нет. Если на боксплоте потенциальные выбросы присутствуют, тогда по графику следует определить их количество и местоположение (максимум/минимум), а затем использовать статистический критерий, например критерий Граббса, для объективной оценки отклоняющихся значений. Если критерий Граббса выявил аномальное значение, то его следует исключить из дальнейшего анализа.
Рассмотрим критерий Граббса для проверки на один выброс. Пусть X1, X2, ..., Xk – упорядоченный по возрастанию ряд наблюдений, в котором
наименьшее значение – X1, а наибольшее – Xk . Обозначим группу образцов без аномальных значений – А, с аномальными значениями – Б. Нулевая гипотеза критерия Граббса: все X1, X2, ..., Xk принадлежат группе А. При проверке на выброс максимального значения альтернативная гипотеза заключается в том, что X1, X2, ..., Xk 1 принадлежат группе А, а Xk – группе Б. В таком случае критерий Граббса имеет вид
G Xk X 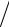 S ,
S ,
где X – среднее выборочное значение; S – стандартное отклонение значений в выборке.
При проверке на выброс минимального значения альтернативная гипотеза предполагает, что X2, X3, ..., Xk принадлежат группе А, а X1 – группе Б. В данном случае критерий Граббса принимает вид
G X X1 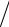 S .
S .
Далее используют табличные значения для соответствующего G критерия и уровня значимости α. Нулевая гипотеза принимается, если G Gтаб, в про-
12
тивном случае она отвергается и принимается альтернативная гипотеза. Существуют критерии Граббса для проверки на аномальность одновременно двух или трех максимальных (минимальных) потенциальных выбросов, а также различных комбинаций количества и типа потенциальных выбросов [2].
1.2.2. Статистические свойства экспериментальных данных
Корректность анализа зависит от соответствия типа критерия статистическим свойствам анализируемых данных, а именно нормальности распределения и однородности дисперсий.
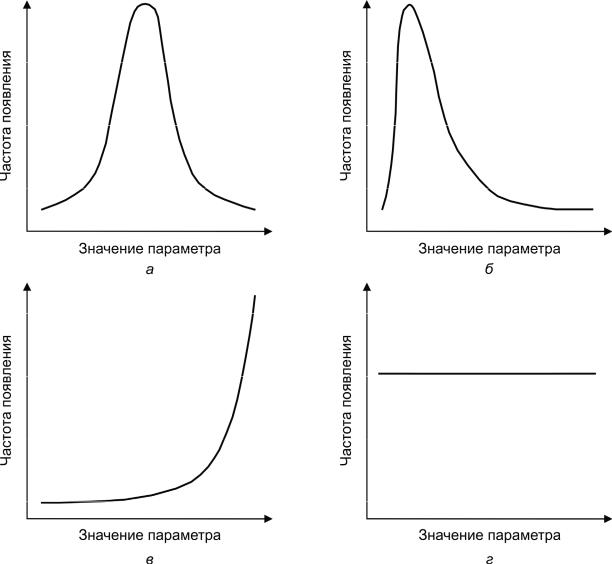
Кривая распределения – график зависимости частоты появления конкретного значения параметра от этого значения. По форме такого графика все виды распределений можно разделить на нормальное и отличное от нормального (логнормальное, экспоненциальное, равномерное и др.) (рис. 1.3).
Рис. 1.3. Виды распределения значений параметра: а – нормальное; б – логнормальное; в – экспоненциальное; г – равномерное
13
Дисперсия определяет степень разброса (изменчивости) данных. Однородность дисперсий (равенство дисперсий в группах, гомоскедастичность дисперсий) является важным условием при применении более мощныхпараметрических критериев.
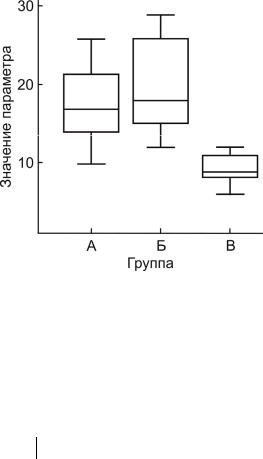
Соблюдение условия однородности дисперсий можно оценить, нарисовав для каждой группы анализируемых данных диаграммы размахов. Неравенство дисперсий полученных выборок данных может быть обусловлено как непосредственно различием в разбросе значений в раз-
ных группах, так и зависимостью погрешности системы измерения от величины значения параметра. На рис. 1.4 представлен пример оценки однородности дисперсий с помощью построения диаграмм размахов. Видно, что дисперсия групп А и Б однородна, а групп Б и В – нет.
В некоторых случаях вид распределения исследуемого параметра и выполнение условия однородности дисперсий можно узнать из литературных источников. Если такие свойства исследуемого параметра не известны или плохо изучены, то лучше использовать непараметрические критерии, чтобы избежать увеличения ошибок принятия гипотез. В случае если свойства измеряемого параметра уже были хорошо изучены и из достоверных источников известно о нормальности распределения параметра и однородности его дисперсий, то следует использовать параметрический критерий.
Статистический анализ позволяет проверить выполнение обоих условий на малых выборках данных. Для того чтобы определить, согласуется ли вид распределения анализируемых совокупностей с нормальным законом, следует использовать специальные критерии нормальности. Для всех критериев нормальности характерна нулевая гипотеза, которая утверждает, что выборка принадлежит группе с нормальным распределением исследуемого параметра. Альтернативная гипотеза – распределение данных отлично от нормального закона.
Один из критериев нормальности, широко используемый в области анализа данных медико-биологических исследований – критерий Шапиро– Уилка. Данный критерий наиболее мощный, когда неизвестен вид альтернативного распределения (если анализируемые выборки данных не принадле-
14

жат нормально распределенным совокупностям) [3]. Значение критерия рассчитывается для каждой выборки отдельно и может быть найдено по формуле (если n 3)
где s2 n xi x 2 ; i 1
|
1 |
|
k |
|
|
|
|
|
2 |
|
W |
|
|
a |
n i 1 |
x |
n i 1 |
x |
|
, |
|
s2 |
||||||||||
|
|
|
|
i |
|
|
||||
|
|
i 1 |
|
|
|
|
|
|
||
x 1 n xi ; k n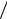 2 ; a – специальные коэффициенты для n i 1
2 ; a – специальные коэффициенты для n i 1
среднеквадратического отклонения Ллойда [3]; n – объем выборки; xi – зна-
чения, принадлежащие выборке; x – среднее значение для выборки. В качестве решающего правила используется табличное значение W-критерия Ша- пиро–Уилка для уровня значимости α [3]. Нулевая гипотеза верна, если рассчитанное значение не меньше табличного (W Wтаб).
Для контроля условия однородности дисперсий в двух выборках данных (при условии, что нет причин сомневаться в выполнении этого условия) предлагается использовать критерий Фишера. Пусть для двух выборок, удовлетворяющих условию нормальности распределения, требуется проверить
гипотезу о дисперсиях H0 : 12 22, опираясь на их несмещенные выбороч-
ные оценки – s12 и s22 . При этом альтернативная гипотеза H1: 12 22. Фор-
мула для критерия Фишера представляет собой отношение двух выборочных оценок дисперсий
s2
F 1 . s22
В числителе принято ставить большую из двух выборочных оценок дисперсий. Тогда при истинности нулевой гипотезы значение критерия F будет иметь распределение Фишера с числом степеней свободы n1 1, n2 1, где
n1 и n2 – размеры сравниваемых выборок данных. Если F F , n1 1, n2 1, то
нет оснований отвергать нулевую гипотезу о равенстве дисперсий в сравниваемых выборках данных.
Если в исследование включены несколько экспериментальных групп, то попарное сравнение дисперсий с помощью критерия Фишера становится неудобным. В этом случае используют критерии контроля однородности дисперсий сразу во всех группах, такие, как критерий Бартлетта или критерий Кохрана при равных объемах выборок [3].
15
Рассмотрим критерий Бартлетта. Пусть s12, s22, , sk2 – выборочные
оценки дисперсий 12, 22, , |
k2 |
по выборкам объема n1, n2, , nk . Тогда |
|||||||||||||||
при сравнении нескольких k 2 |
дисперсий нулевая и альтернативная гипо- |
||||||||||||||||
тезы объективного критерия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
H0 : i2 2j , |
|
|
|
|
|
||||||
|
|
H |
|
: |
2 |
2 |
(для i j ). |
|
|
||||||||
|
|
1 |
|
i |
|
j |
|
|
|
|
|
|
|
|
|||
Для ni |
3 (i 1, , k |
– номер группы) критерий Бартлетта может быть |
|||||||||||||||
рассчитан по формуле [3] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
k |
1 |
|
|
1 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
B M 1 |
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
n 1 |
|
||||||||||||
|
|
|
|
|
3 k 1 |
|
|
N |
|
|
|||||||
|
|
|
|
|
|
|
i 1 |
i |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
ni 1 ln si2 , |
|||||||
|
M N ln |
|
|
|
i 1 si2 |
||||||||||||
|
|
|
|||||||||||||||
|
|
N |
i 1 |
|
|
|
|
i 1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
k |
ni 1 ; si2 – несмещенная оценка дисперсии для i группы; ni – |
||||||||||||||||
где N |
|||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
размер i выборки. При истинности нулевой гипотезы данный критерий имеет распределение 2 с k 1 степенями свободы. Нулевая гипотеза верна, если
B Bкр, , k 1.
Стоит отметить, что мощность критериев нормальности распределения и однородности дисперсий применительно к малым выборкам очень мала (т. е. вероятность ошибки второго рода очень высока) [1]. Поэтому, если до начала анализа результатов эксперимента известно, что или распределение значений исследуемого параметра для биологических объектов какой-либо из экспериментальных групп не подчиняется нормальному закону, или дисперсии в каких-либо парах групп не могут быть равными, или имеет место один из следующих факторов:
–наличие значительных отклонений значений измеряемого параметра в анализируемых выборках, отражающих действительный разброс;
–нелинейный характер ошибки измерительного устройства;
–некорректно выполненный этап планирования исследования, например, отсутствие рандомизации при отборе биологических объектов в группы,
16
то к таким данным сразу следует применять непараметрические критерии. Таким образом, проверка полученных выборок данных на нормальность распределения и однородность дисперсий позволяет выявить лишь грубые нарушения требуемых условий.
1.3. Методы оценки статистически значимых различий между группами
Распространенной задачей медико-биологических исследований является сравнение значений некоторого параметра между несколькими группами биологических объектов. Для этих целей принято использовать критерии оценки значимости различий. Все критерии, относящиеся к данной группе, имеют одинаковую нулевую гипотезу – значимых различий в значении исследуемого параметра между экспериментальными группами нет, и альтернативную гипотезу – значения исследуемого параметра в экспериментальных группах значимо различаются.
В зависимости от схемы эксперимента измеренные значения параметра могут быть связанными (зависимыми, парными) или несвязанными (независимыми, непарными). Если в разные экспериментальные группы входят разные биологические объекты, например здоровые и больные, у которых измерен один и тот же параметр, то такие данныеявляются несвязными (табл. 1.1).
|
|
Таблица 1.1 |
|
Схема эксперимента с несвязными данными |
|
|
|
|
Группа |
Номер биологического объекта |
Значение параметра |
Здоровые |
1 |
1.67 |
|
2 |
1.12 |
|
3 |
3.55 |
|
4 |
6.43 |
Больные |
5 |
7.11 |
|
6 |
3.14 |
|
7 |
8.23 |
|
8 |
5.98 |
Если в разные экспериментальные группы входят одни и те же биологические объекты, но в разных состояниях, например больные до и после лечения, или если у одних и тех же объектов измеряется несколько разных параметров, то такие данные будут связными (табл. 1.2).
Объемы выборок для связанных данных должны совпадать n1 n2 n .
Кроме этого массив связанных данных должен содержать информацию о принадлежности измеренных значений конкретному биологическому объек-
17

ту. Это может быть реализовано посредством упорядочивания данных в группах таким образом, чтобы значения параметров, соответствующие одним и тем же объектам, имели одинаковые порядковые номера.
|
|
Таблица 1.2 |
Схема эксперимента со связными данными |
||
|
|
|
Номер биологического |
Значение параметра |
|
объекта |
Группа образцов до лечения |
Группа образцов после лечения |
1 |
4.37 |
1.05 |
2 |
5.62 |
2.39 |
3 |
7.21 |
3.65 |
4 |
3.13 |
2.84 |
Тогда анализ различий сводится к расчету критерия для одной выборки, полученной путем расчета разностей для каждой пары связных значений Zi X1i X 2i . Такие критерии называются одновыборочные или парные
(one-sample test). Для анализа несвязанных данных применяются двухвыборочные критерии (two-sample test). Тип используемого критерия должен соответствовать схеме эксперимента.
1.3.1.Критерии сравнения нескольких групп
Краспространенным задачам анализа также относится поиск ответа на вопрос: есть ли среди нескольких экспериментальных групп хотя бы одна,
вкоторой значения измеренного параметра отличаются от значений в остальных группах? Для решения такой задачи применяются критерии по одновременному сравнению всех групп между собой, например параметрический критерий F (дисперсионный критерий, one-way ANOVA test) или его непараметрический аналог – H-критерий Краскела–Уоллиса.
Дисперсионный критерий F основан на разделении общей изменчивости
данных на межгрупповую изменчивость Sмеж2 , которая описывает степень различия между экспериментальными группами, и внутригрупповую изменчивость Sвн2 , описывающую величину случайных различий между индивиду-
альными образцами в пределах каждой группы. При этом изменчивость данных описывается дисперсией и находится по формулам
Sмеж2 n j |
|
j |
|
общ 2 , |
X |
X |
|||
j |
|
|||
Sвн2 Xij X j 2 ,
j i
18
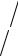
где j 1, 2, , k номер группы (k – число групп); n j – число |
измерений для |
|||
j-й группы; |
|
j – среднее значение параметра для j-й группы; |
|
общ – общее |
X |
X |
|||
среднее (среднее значение по средним для всех групп); i 1, 2, , n j – номер измерения в пределах j-й группы; Xij – значение параметра для i-го образца
и j-й группы; N – общее число измерений по всем группам вместе. Критерий F для любых n j 1 и k 1 представляет собой отношение
этих двух дисперсий и рассчитывается по формуле [1]:
|
2 |
|
|
|
F |
Sмеж |
|
k 1 |
. |
S вн2 |
|
|
||
|
N k |
|||
При условии истинности нулевой гипотезы F-критерий имеет распределение Фишера с k 1 и N k степенями свободы. Нулевая гипотеза принимается, если F Fкр для требуемого уровня значимости.
Известно, что дисперсионный критерий неустойчив даже к небольшим отклонениям распределения данных от нормального закона и к различиям дисперсий между сравниваемыми группами [1]. Поэтому если условия нормальности распределения или равенства дисперсий не удовлетворены, то необходимо использовать непараметрический H-критерий Краскела–Уолли- са. Значение критерия H рассчитывается по формуле
|
12 |
k R2j |
|
|
|
|
|
H |
|
j 1 |
|
3 |
|
N 1 |
, |
N N 1 |
n j |
|
|||||
k
где N n j – общее число наблюдений во всех k группах; R j – сумма ран- j 1
гов наблюдений из группы j; n j – число наблюдений в группе j.
Критерий H может быть рассчитан для k 2 и n j 2. Если H Hкр для
требуемого уровня значимости α, то нулевая гипотеза верна.
Особенностью F- и H-критериев является то, что при отклонении нулевой гипотезы и принятии ее альтернативы нельзя узнать, какие конкретно пары групп отличаются. Именно поэтому данные критерии следует использовать только для оценки наличия эффекта от экспериментального воздействия хотя бы на одну группу. Чтобы определить, отличаются ли конкретные пары групп, необходимо последовательно выполнить несколько соответ-
19
ствующих парных сравнений с помощью методов сравнения двух групп описанных в следующем разделе.
1.3.2. Критерии сравнения двух групп
Графический метод сравнения двух групп. Суть данного метода заклю-
чается в изображении на одном графике оценок средних значений и их 95 %-х доверительных интервалов для каждой выборки данных. Оценку группового среднегозначения можно найти дляj-й выборки данных объемом n j как
n j
X j xi n j , i 1
где xi – значения, принадлежащие j-й выборке данных. Доверительный ин-
тервал среднего значения содержит истинное среднее значение параметра с заданной вероятностью. Границы доверительного интервала можно найти
как |
|
|
|
|
|
, где X j t , df s j |
n j , а t , df – коэффици- |
|
|
||||||
X j X j ; |
X j X j |
||||||
ент Стьюдента, характеризующий степень доверия полученному значению оценки среднего для выборки; α – уровень значимости коэффициента (для двухстороннего критерия Стьюдента α = 0.025 определяет 95 %-й доверительный интервал); df n j 1 – число степеней свободы критерия Стьюден-
|
n |
|
||
та; s j |
j xi |
|
j 2 |
n j 1 |
X |
||||
|
i 1 |
|
||
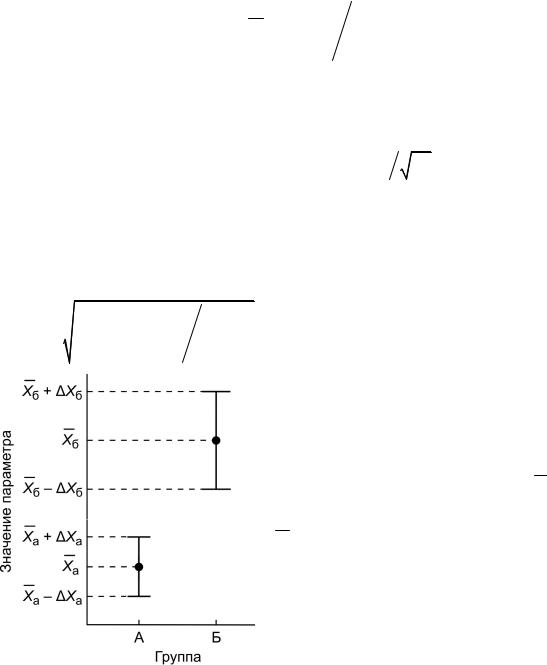
Рис. 1.5. Графический метод сравнения двух выборок данных
– оценка выборочного стандартного откло-
нения (формула для малых выборок). Значения коэффициента Стьюдента для разных α и df можно узнать в специальных таблицах. На рис. 1.5 показан пример изображения средних значений X j (точки)
и доверительных интервалов средних X j X j (линии с ограничениями) пара-
метра X для двух групп.
Стоит отметить, что доверительный интервал корректно рассчитывать только в отношении нормально распределенных совокупностей. Кроме того если измерений в группе мало (2–3), то доверительный ин-
20
