
Манило (метода)
.pdf
тервал сильно увеличивается. Увеличение доверительного интервала при уменьшении количества измерений связано с ростом соответствующего коэффициента Стьюдента.
Если доверительные интервалы на графике не пересекаются, то можно сделать заключение, что значения исследуемого параметра для экспериментальных групп значимо различаются. Если же доверительные интервалы пересекаются, то нельзя утверждать, существуют или нет различия между сравниваемыми группами. Таким образом, графический метод позволяет выявить только очевидные различия. Для того чтобы выявить малые различия или признать, что они отсутствуют, необходимо использоватьобъективные критерии.
Объективные критерии сравнения двух групп. Для объективнойоценки наличия различий между парами групп существует ряд статистических критериев. Выбор между параметрическими или непараметрическими критериями определяется свойствами данных, а выбор между критериями для связанных данных или независимых выборокопределяется схемой эксперимента.
Двухвыборочный критерий Стьюдента (t-критерий). Данный пара-
метрический критерий используется для анализа различий между двумя группами независимых значений. Для использования t-критерия Стьюдента требуется, чтобы минимальное количество измерений в каждой выборке данных было не менее двух. Значение t-критерия рассчитывается по формуле
t |
|
X |
1 |
X |
2 |
|
n1 n2 |
, |
|
|
|
s |
|
||||||
|
|
|
|
n |
n |
|
|||
|
|
|
|
|
|
|
1 |
2 |
|
s2 n1 1 s12 n2 1 s22 , n1 n2 2
где X 1 , X 2 – средние значения для выборок X1 и X 2 соответственно; n1 и n2 – объемы выборок; s2 – обобщенная дисперсия; s12 и s22 – несмещенные
оценки дисперсии для исследуемых групп.
При справедливости нулевой гипотезы непарный t-критерий имеет распределение Стьюдента с числом степеней свободы df n1 n2 2 . Различия
между двумя группами признаются значимыми, если t tdf для заданного
уровня значимости.
Существует способ, который позволяет внести поправку на неравенство дисперсий двух сравниваемых групп и использовать параметрический t-кри- терий. При неравных дисперсиях t-критерий рассчитывается по формуле
21

t |
|
X |
1 |
X |
2 |
|
. |
||
s2 |
n |
s2 |
n |
||||||
|
1 |
|
1 |
2 |
2 |
|
|||
Кроме того необходимо сделать поправку на число степеней свободы. Существует несколько видов поправок, ниже приведена поправка Уэлча– Сатервайта
|
|
|
s2 |
n |
s2 |
n |
2 |
2 |
|
|
|
||
df |
|
|
1 |
1 |
2 |
|
|
|
|
|
|
. |
|
s2 |
n 2 |
n |
1 s2 |
n |
2 |
2 |
n |
1 |
|||||
1 |
1 |
1 |
|
|
2 |
|
|
|
2 |
|
|
||
Парный t-критерий. Данный параметрический критерий используется для анализа различий между двумя группами зависимых значений. Минимальное число пар, которое допускает критерий, равно двум. Пусть имеются две связанные выборки данных. Тогда t-критерий рассчитывается для одной выборки Zi X1i X 2i по формуле
t sZz n,
где Z – среднее значение для полученных разностей; sz – несмещенное стандартное отклонение для Zi ; n – количество значений в полученной совокупности Zi .
При справедливости нулевой гипотезы парный t-критерий подчиняется распределению Стьюдента с числом степеней свободы df n 1. Различия
признаются значимыми, если t tdf для заданного уровня значимости.
Критерий U Манна–Уитни. Непараметрической альтернативой критерию t для анализа различий между двумя группами независимых значений является критерий Манна–Уитни (U-критерий, критерий ранговых сумм, Wilcoxon rank sum test). Использование критерия U возможно только, когда количество значений в каждой из выборок не менее трех. В одной выборке может быть два значения, но тогда во второй их должно быть не менее пяти [4]. Значение критерия рассчитывается по формуле
U min U1, U2 ,
U1 R1 n1 n1 1  2 , U2 R2 n2 n2 1
2 , U2 R2 n2 n2 1  2 ,
2 ,
где n1 и n2 – количество образцов для групп 1 и 2 соответственно; R1 , R2 – суммыранговзначенийизпервойивторойгрупп(вобщемупорядоченномряду).
22
Различия признаются значимыми, если U Uкр для заданного уровня значимости и объемов выборок n1 и n2 .
Существует аппроксимация распределения U-критерия нормальным законом, которая может быть использована для расчета p значений при больших объемах выборок.
Парный T-критерий Вилкоксона (критерий знаковых рангов, Wilcoxon signed rank test). Данный непараметрический критерий применяется для анализа различий между двумя группами зависимых значений. Минимальное количество пар значений не должно быть меньше пяти. Если в упорядоченном ряду Zi есть нулевые значения, то их следует исключить и пересчитать
объем выборки n [5]. Далее критерий T находится как
|
T min T , T , |
где T – |
сумма рангов тех Zi, для которых выполняется неравенство |
X1i X 2i ; |
T – сумма рангов тех Zi, для которых выполняется неравенство |
X1i X 2i . |
Различия признаются значимыми, если T Tкр для заданного |
уровня значимости и объема выборки n.
Существует аппроксимация распределения T-критерия нормальным законом, которая может быть использована для расчета p значений при больших объемах выборок.
Односторонний (one-tailed) и двухсторонний (two-tailed) критерии.
Если заранее неизвестно возможное направление изменения значения параметра в одной группе по сравнению с другой, то для определения значимости различий следует применять двухсторонние критерии. При использовании двухстороннего критерия учитывается то, что однозначно неизвестно, какая из двух сравниваемых групп имеет большие значения исследуемого параметра при отклонении нулевой гипотезы, т. е. для определения критического значения критерия необходимо использовать α/2.
Однако некоторые исследования направлены на проверку однонаправленного изменения значения параметра (т. е. только увеличение или только уменьшение) в первой группе по сравнению со второй. В этом случае лучше использовать односторонний критерий, что не требует деления пополам уровня значимости и поэтому позволяет увеличить мощность используемого критерия, тем самым уменьшая количество упущенных критерием значимых различий [1].
23
Множественные сравнения. Часто на практике при статистическом анализе данных возникает необходимость оценить значимость различий значения некоторого исследуемого параметра в более чем двух группах или сравнить группы по более чем одному параметру. При этом группы сравниваются попарно (каждая с каждой или каждая с контрольной группой), и ко всем парам групп применяется один из критериев значимости различий. Такие задачи являются классическим примером множественных сравнений и многократное использование какого-либо критерия, предназначенного для сравнения двух групп, вызывает так называемый эффект множественных сравнений, при котором увеличивается суммарная ошибка первого рода для всего исследования [6].
Например, ставится задача сравнить попарно четыре несвязанные выборки данных, используя для каждой пары критерий Манна–Уитни, т. е. число
сравнений равно q k! 2 k 2 4!
2 k 2 4! 2 4 2 6. Если для каждого из ше-
2 4 2 6. Если для каждого из ше-
сти сравнений установить вероятность ошибки первого рода критерия равной 5 %, то для всего исследования вероятность ошибки первого рода составит
P 1 1 q 1 1 0.05 6 0.2649, что гораздо больше 0.05. Аналогичным образом рассчитывается групповая ошибка и при анализе связанных данных, только критерий для анализа различий используется парный. Таким образом, при увеличении числа сравниваемых групп точность результатов исследования уменьшается. Поэтому необходимо вводить поправку на уровень значимости, чтобы в итоге получить вероятность ошибки всего исследования 5 % или скорректировать уже полученные значения. Рассмотрим наиболее часто используемые методы для учета эффекта множественных сравнений.
Если число необходимых сравнений мало q 8 , то можно применить
наиболее простой в использовании метод – поправку Бонферрони, который основан на контроле суммарной вероятности ошибки первого рода для всех проводимых сравнений. Поправка вводится для заданного исследователем уровня значимости используемого критерия таким образом, что  q , где α –
q , где α –
требуемый уровень значимости, q – число необходимых сравнений. Также поправка может быть введена и для полученных p-значений, путем их умножения на q. При этом правило принятия нулевой гипотезы сохраняется, так же как и остается прежним требуемый уровень значимости, но уже используются скорректированные p-значения. Стоит отметить, что поправка Бонферрони не зависит от того, какие данные анализируются – связанные или несвязанные, поэтому может быть применена и в обоих случаях.
24

В случае большего числа сравнений q 8 данный метод не позволяет
признать значимыми даже вполне очевидные различия между группами. В таком случае необходимо использовать поправку Беньямини–Хохберга. Особенность данного метода заключается в том, что он допускает определенное количество ложных отклонений нулевой гипотезы. Рассмотрим методику внесения поправки Беньямини–Хохберга. Полученные p-значения упорядочивают по возрастанию, причем i 1, 2, , q – порядковый номер p-зна-
чения в таком ряду. В соответствии с данным методом решающее правило для принятия нулевой гипотезы об отсутствии значимых различий между двумя группами при использовании поправки к уровню значимости
H0 : pi qi , H1 : pi qi
или при использовании поправки для p значений
H0 : pii q , H1 : pii q .
Для практического применения поправки Беньямини–Хохберга необходимо, чтобы p-значения, полученные для разных пар групп, были независимыми [7]. Это выполняется, если проводится анализ несвязанных данных. Если число сравнений больше восьми и анализируемые данные – связанные, то необходимо использовать другой метод – Беньямини–Йекутили. Он похож на поправку Беньямини–Хохберга, отличие состоит лишь во введении дополнительного множителя в поправке. Решающее правило для принятия нулевой гипотезы об отсутствии значимых различий между двумя группами при использовании поправки Беньямини–Йекутили к уровню значимости
H |
0 |
: p |
|
|
i |
|
|
|
, |
||
|
|
|
|
|
|||||||
|
i |
|
|
q |
|
q |
1 i |
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
H |
1 |
: p |
|
i |
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
i |
|
|
q |
|
q |
1 i |
|||
|
|
|
|
|
|
|
|
|
|||
i 1
25
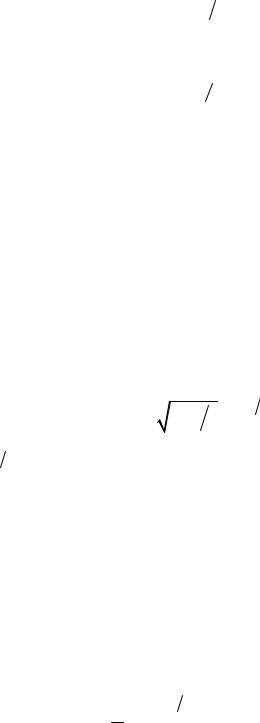
или при использовании поправки для p-значений
|
|
|
q |
|
1 i |
||
|
|
|
pi q |
||||
H0 |
: |
|
i 1 |
|
|
, |
|
|
i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
q |
1 i |
|||
|
|
|
pi q |
||||
H1 |
: |
|
i 1 |
|
|
|
. |
|
i |
|
|
|
|||
|
|
|
|
|
|
|
|
Объем выборки и мощность критерия значимости различий. Прежде чем применять статистический критерий нужно ответить на вопрос: ошибки какого рода критичнее для конкретного исследования. Если требуется обнаружить только очевидные различия между группами данных, то достаточно следить за тем, чтобы уровень значимости не превышал выбранного порога. Если важно не пропустить все возможные существующие различия, то нужно контролировать мощность критерия на требуемом исследователем уровне. Например, для расчета мощности t-критерия нужно найти квантиль распределения Стьюдента по формуле(приодинаковыхобъемахвыборокданныхравныхn) [1]
|
t 1 , 2 n 1 |
|
|
|
|
|
|
t 2, 2 n 1 |
|
, |
|
|
|
|
|||||||
|
|
2s2 n |
|
|
||||||
где t 1 и t 2 – |
|
|
|
|
|
|
|
|
||
табличные |
значения |
для распределения Стьюдента |
||||||||
df 2 n 1 ; 1 |
и α – мощность и требуемый уровень значимости крите- |
|||||||||
рия; δ – обнаруживаемая критерием разница между средними значениями
параметра в исследуемых биологических группах (величина эффекта); s2 – обобщенная оценка дисперсии для сравниваемых групп данных (при выпол-
нении условия однородности дисперсий 12 22 2 ), рассчитываемая как отношение суммы квадратов отклонений значений выборок от их выборочных средних значений к значению n1 n2 2.
Для одностороннего критерия t 2 заменяется на t . Для связных дан-
ных величина эффекта равна Z , а s sz . Затем в соответствии с полученным значением необходимо определить по стандартным таблицам квантилей Стьюдента вероятность ошибки второго рода и рассчитать мощность как1 . При неравных объемах выборок данных для расчета мощности критерия используется значение n 2n1n2 n1 n2 [1].
n1 n2 [1].
26
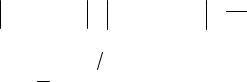
Если разница между значениями регистрируемого параметра в исследуемых группах мала, а внутригрупповой разброс значений достаточно велик, то мощности критерия может быть недостаточно, чтобы обнаружить реально существующие различия. В таком случае требуемого уровня мощности можно добиться, увеличив размер выборки. Для независимых измерений размер каждой из двух выборокданных может бытьрассчитан по формуле [1]
2 s2 n 2 t  2, 2 n 1 t 1 , 2 n 1 2 .
2, 2 n 1 t 1 , 2 n 1 2 .
Для одностороннего критерия t 2 заменяется на t . Для связных дан-
ных величина эффекта равна Z , а s sz . Если измерения параметра еще не проведены, то расчет размера выборки позволяет корректно составить план эксперимента либо отказаться от проведения измерений, если требуемое количество образцов слишком велико. Также стоит отметить, что расчет размера выборки или мощности критерия значимости различий проводится только в предположении, что выборки получены из нормально распределенных совокупностей, к тому же дисперсии сравниваемых групп данных должны быть статистически равны.
1.4. Анализ диагностических признаков
Задачей исследования может быть поиск классификатора – параметра, на основании значения которого объект может быть отнесен к одной из биологических групп, например больным или здоровым. Ясно, что не в каждом исследовании есть такие группы биологических объектов. Тем не менее, считается, что та биологическая группа, объекты из которой имеют бо́льшие значения исследуемого параметра, служат носителями некоторого признака, который и выявляет классификатор (например, наличие некоторой болезни).
Для того чтобы оценить возможность параметра разделять две биологические группы объектов, а также оценить качество разбиения, т. е. то количество ошибок, которое допускает классификатор, вводят понятия чувствительность и специфичность. Если классификатор нацелен на выявление подгруппы «больные» в группе, включающей и «больных» и «здоровых», то чувствительность – это доля объектов из группы «больные», которых классификатор отнес к больным, а специфичность – это доля объектов из группы «здоровые», которых классификатор отнес к здоровым.
27
Выполнив выборочные измерения исследуемого параметра для объектов из двух биологических групп (т. е. заранее известна принадлежность каждого объекта к определенной биологической группе), можно рассчитать чувствительность и специфичность классификатора для любого значения параметра, который в этом случае является порогом классификации. Для наглядного представления характеристик классификатора удобно использовать ROC (Receiver Operating Characteristic) кривую – график, отображающий соотноше-
ние между специфичностью классификатора и его чувствительностью для различных значений порога классификации. По оси X графика откладывается величина (1-специфичность), а по оси Y – значение чувствительности для текущего значения порога (рис. 1.6, б). Для любого классификатора ROC-кривая начинается в точке с координатами (0; 0) для максимального значения порога классификации, а заканчивается в точке с координатами (1; 1) для минимального значения порога классификации. Идеальный классификатор – это кривая, проходящая через точку с координатами (0; 1), а диагональ, соединяющая точки с координатами (0; 0) и (1; 1) – бесполезный классификатор.
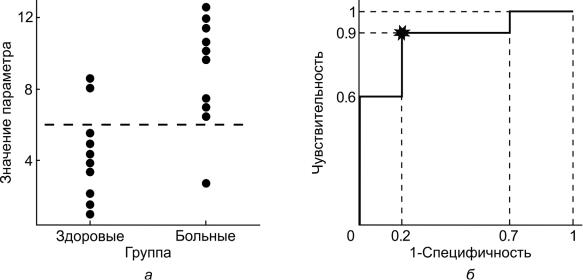
Рассмотрим принцип построения ROC-кривой на примере распределения значений некоторого параметра в группах «здоровые» и «больные», которое изображено на рис. 1.6, а.
Рис. 1.6. Принцип построения ROC-кривой
При некотором значении порога классификации классификатор предполагает, что образцы, значение параметра для которых больше порога, относятся к группе «больные», а образцы, значение параметра для которых меньше порога, относятся к группе «здоровые». Таким образом, для данного значения
28
порога классификации, который обозначен штриховой линией на рис. 1.6, а и звездочкой на рис. 1.6, б, специфичность = 80 %, так как восемь из десяти здоровых верно отнесены классификатором к группе «здоровые», а чувствительность = 90 %, так как девять из десяти больных верно отнесены классификатором к группе «больные».
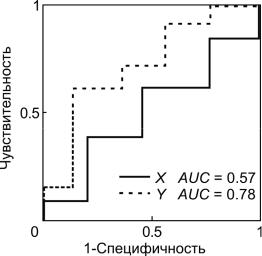
С помощью анализа ROC-кривых можно сравнивать эффективность нескольких разных классификаторов для одних и тех же групп объектов. Для этого необходимо
на одном графике построить ROC-кривые для каждого из классификаторов. На рис. 1.7 представлены ROC-кривые для классификаторов X и Y. Кривая для классификатора Y расположена выше и левее, что свидетельствует о его большей эффективности.
В случае пересечения кривых сравнительный анализ можно проводить, используя показатель AUC (Area Under ROC Curve) – площадь под ROCкривой. Данный показатель дает количественную оценку эффективности классификатора. Чем выше показатель AUC, тем качественнее классификатор, при этом для бесполезного классификатора AUC = 0.5, а для идеального классификатора AUC = 1.
1.5. Анализ зависимости двух параметров
Еще одной из задач исследования может быть поиск связи между двумя разными медико-биологическими параметрами, значения которых измерены у одних и тех же биологических объектов.
Если при изменении одного параметра другой также изменяет свое значение по определенному, часто неизвестному, закону, считается, что между параметрами существует связь. Следует отметить, что наличие связи между двумя параметрами может указывать на зависимость одного из них от второго или зависимость от некоторого третьего общего регулирующего фактора. Поэтому проверка существования связи между измеренными параметрами и определение ее вида позволяет получить дополнительную информацию о функциональных связях между компонентами изучаемой системы.
29
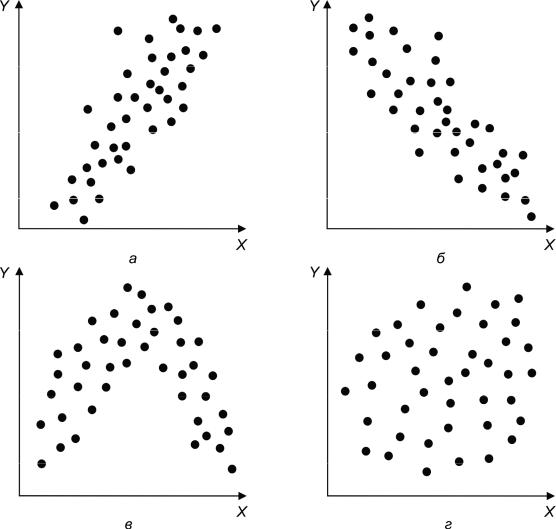
Рис. 1.8. Виды зависимости двух параметров X и Y: а, б – линейная зависимость; в – нелинейная зависимость; г – отсутствие зависимости
Связь бывает двух видов – линейная, при которой зависимость между переменными может быть описана линейной функцией, и нелинейная, которая описывается с помощью нелинейной (квадратичной, кубической или др.) функции. Чтобы оценить вид связи, можно построить скатерограмму – график зависимости одной переменной от другой (рис. 1.8). Точка на таком графике – это конкретный объект, а координаты точки – значения параметров X i и Yi для этого объекта.
Корреляционный анализ представляет собой объективный метод анализа связи между двумя параметрами и позволяет количественно описать связь с помощью коэффициента корреляции (r) – характеристики степени связи, выраженной одним числом. Коэффициент корреляции принимает значения от –1 до +1. Чем сильнее связь между переменными, тем больше абсолютное значение коэффициента корреляции, r = 0 говорит об отсутствии связи. Знак r
30
