6. Простейший поток вызовов

_{Поток вызовов – с.п.}

Первое определение простейшего потока:

Поток вызовов называется простейшим, если выполняются 3 условия:

1. - марковский;

2. Вероятность поступления ровно k вызовов в промежутке времени длиной t не зависит от начального момента этого промежутка (условие стационарности);

3. , k = 0,1,…; , - параметр простейшего потока.

Эти 3 условия однозначно характеризуют структуру простейшего потока с точностью до параметра .

Комментарии к условиям:

Условие 1. Марковость означает отсутствие последействия.

Условие 2. Промежуток t может быть расположен в любом месте временной оси.

~ _{-равносильны, один и тот же закон распределения.}

Если для марковского процесса выполняется условие 2, то он стационарен.

Условие 3.Число вызовов в промежутке длины t распределено по закону Пуассона с параметром .

Следовательно: а) среднее число вызовов в промежутке длины t.Коэф.пропор

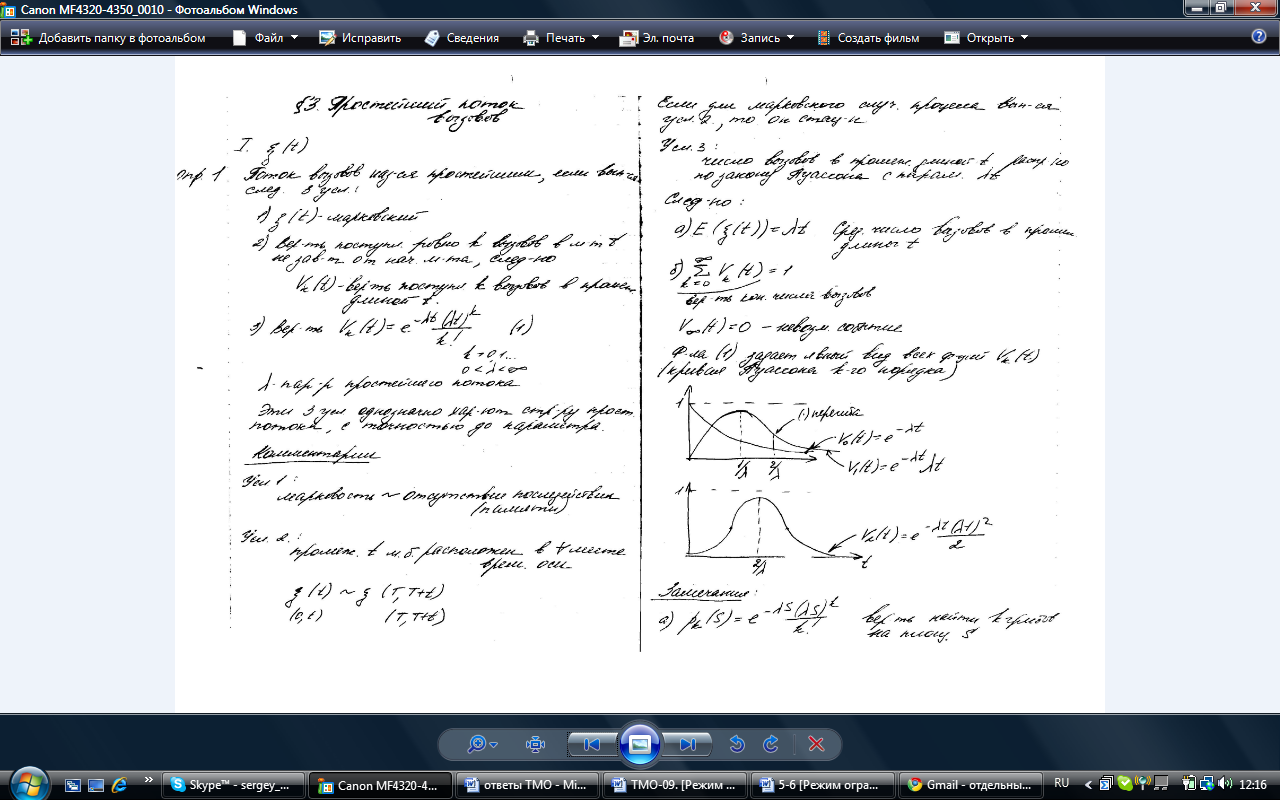
б) вероятность конечного числа вызовов; (невозможность события)

– Кривая Пуассона -го порядка.

Два простейших потока могут

отличаться

друг от друга только значением

параметра.

Интенсивностью стационарного потока называется среднее число вызовов, поступающих за промежуток времени единичной длины .

Применение: Среднее число вызовов в промежутке пропорционально длине этого промежутка, причем является коэффициентом пропорциональности.

Доказательство: Пусть , разобьем на промежутки единичной длины: рисуем.

1. 

2. 

ч. т. д.

Свойства простейшего потока:

A)

Доказательство (2 варианнта):

1. 

B) Средняя длина промежутка между последовательными вызовами равна

( )

Расчет или для простейшего потока:

1. Наблюдаем за случайной величиной

2. Регистрируем реальные значения этой величины: ―результат iого наблюдения (в iый промежуток ед. длины)

3. Среднее арифметическое этих наблюдений:

Второе определение простейшего потока:

Поток вызовов называется простейшим, если для него выполняется следующее:

1. - марковский;

2. - последовательность независимых случайных величин;

- длина промежутка времени между моментами поступления i-1 и i вызова.

3. Все одинаково распределены по одному и тому же закону, для .

Интенсивность простейшего потока совпадает с параметром ).

.

Замечания:

1. Можно проверить, что оба определения простейшего потока равносильны.

2. Хинчин: простейшим является поток, который складывается из достаточно большого числа отдельных (частных) потоков, поступающих из независимых источников.

Примеры простейших потоков:

1. Поток вызовов на АТС;

2. Поток судов, прибывающих в данный порт;

3. Поток поломок (телевизоров).