17.Пгр и стационарное решение для систем с ожиданием

Пусть n- количество линий в пучке.

Входящий поток - простейший с параметром λ; время обслуживания распределено показательно с параметром β. Множество состояний СО – счётно.

0, 1, 2, …, k, … - состояния СО

а) k≤ n – состояние СО можно определить как количество занятых линий, либо как количество вызовов на обслуживании.

Если занято k линий, то в системе (n-k) свободных линий.

б) k≥ n, следовательно, N(t)=k, то есть, заняты все n линий пучка, k-n вызовов в очереди.

ПГР и Стационарное решение: Для систем с ожиданием -марковский ПГР с параметрами λ_k=λ; (k≥0);

Доказательство:

1. – марковский. Существует Р_ki(τ)

2. -ПГР. Параметры его соответствуют указанным в (1).

Переходные вероятности:

1. 

2. 

Докажем это:

Если k ≥ n

3. 

– 0 вызовов для простого потока, W₀(τ) – 0 освобождений.

.

Стационарное решение.

Замечание: в случае получаем геометрическую прогрессию со знаменателем .

Пусть n=1, следовательно, геометрическая прогрессия со знаменателем .

( )

Если k ≤ n, ;

Если ,

ρ₀ остается неизвестным .

Нормировочное условие:

1=

Считаем, что ⇒ ряд сходится.

p₀ = - 0 вызовов в системе, все линии простаивают.

Замечание: если n=1, – вероятность того, что все линии свободны, а

18.Поведение очереди в системах с ожиданием

p₀ = .

Варианты:

1. . Геометрическая прогрессия сходится, 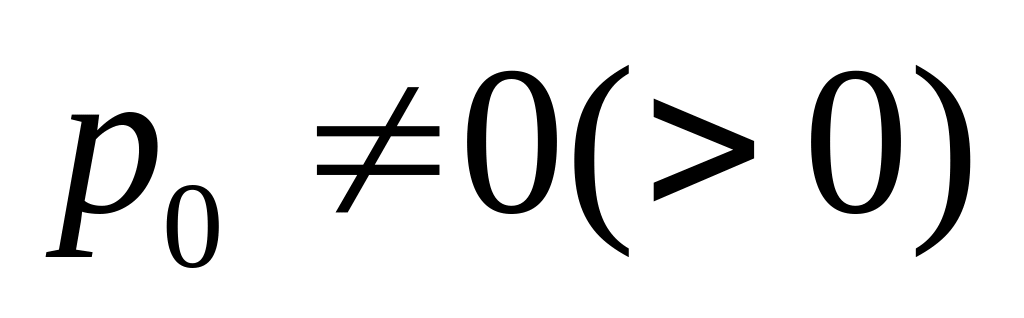, следовательно, .

_{Система справляется с обслуживанием всех поступающих вызовов. Очередь ведет себя естественным образом, колеблется.}

Физический смысл условия : - среднее число вызовов за единицу времени, т.е. интенсивность входящего потока, абсолютная пропускная способность, - номинальная пропускная способность системы обслуживания.

Система справляется с обслуживанием, если в СО поступает чуть меньше вызовов, чем она может обслужить.

Всегда должен быть запас «прочности».

Пример: на производстве – резервные станки, резервные заделы деталей.

2. . , .

С течением времени очередь только увеличивается, система не справляется с обслуживанием входящего потока.

Замечание: Очередь тоже растет неограниченно еще и при (не только )..

- планирование на пределе возможностей.

19.Распределение времени ожидания в системе с ожиданием

Пусть ― время ожидания обслуживания (время в очереди, затраченное каждым клиентом ― случайная неотрицательная непрерывная величина). ― функция распределения для ― вероятность того, что вызову придется стоять в очереди.

Состояния: , .

Пусть ― вероятность при условии того, что вызов застал систему в состоянии k.

при .

Пусть k-n=m ― длина очереди в состоянии k, тогда: ― вероятность при условии того, что все линии пучка заняты и имеется вызовов. Ждать больше времени придется, когда за произойдет освобождений линий.

― вероятность того, что за с момента поступления вызова произойдет освобождений. (то есть освобождений за ).

.

Тогда:

20.Показатели эффективности систем с ожиданием

1. Среднее число занятых линий.

Пусть случайная величина ― число занятых линий.

Вероятности:

так как

Смежные показатели : а) Среднее число свободных линий: .

б) Коэффициент загрузки (линии или СО): ― знаменатель геометрической прогрессии.

2. Смежный показатель

Замечание: в стационарном режиме для каждого вызова 2 возможности с постоянными вероятностями: попадание в очередь с вероятностью ; немедленное обслуживание с вероятностью

Простейшие потоки с параметрами и

3. Среднее время ожидания обслуживания (среднее время в очереди). ―сл. вел. ― функция распределения.

так как легко показать, что

4. Среднее время пребывания вызова в СО

― время пребывания вызова в СО,

с ростом n.

5. Средняя длина очереди. ― длина очереди.

Среднее число вызовов в СО: ― число вызовов в СО.