Билет №1

1) Напряженность электрического поля.

Напряженность эл. поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля 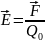. Напряженность поля точечного заряда 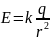, где .

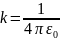2) Электростатическое поле.

Электростатическое поле существует там, где есть неподвижные электрические заряды.

Электрический заряд создает особую форму материи - электрическое поле, посредством которого осуществляется взаимодействие между электрическими зарядами. Электрическое поле порождается только зарядом, а также действует только на заряд.

3) Электрический заряд и его свойства.

Заряд проявляет себя именно в том, что создает поле и взаимодействует с ним.

В природе существует два вида электрических зарядов: положительные и отрицательные, причем это деление чисто условное.

Одноименные заряды отталкиваются, а разноименные притягиваются.

Условно считают, что электрон обладает отрицательным элементарным зарядом (е = - 1,6 · 10^-19 Кл), а протон – положительным.

Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда.

Закон сохранения электрического заряда: ∑q_i = const. Алгебраическая сумма эл. зарядов любой замкнутой системы остается всегда неизменной. Количество положительного и отрицательных зарядов во вселенной одинаково.

Электрический заряд не зависит от того, движется он или покоится, т.е. он инвариантен по отношению к системе отсчета.

4) Точечный электрический заряд.

Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

5) Закон взаимодействия точечных зарядов.

Кулон опытным путем установил, что сила взаимодействия двух точечных электрических зарядов, находящихся в вакууме, прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой, соединяющей заряды (Закон Кулона).

Величина силы взаимодействия точечных зарядов q₁ и q₂:

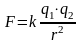, где – коэффициент пропорциональности в системе единиц СИ, ε₀ - электрическая постоянная, равная ε₀ = 8,85 ·10^-12 Ф/м, r – расстояние между зарядами. В векторном виде:

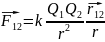
6) Силовые линии электрического поля.

Силовыми линиями называют кривые, касательные к которым в каждой точке совпадают с вектором напряженности 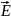. Вектор напряженности показывает направление силовых линий и величину и интенсивность эл. поля в данной точке.

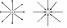
7) Принцип суперпозиции электрических полей, его применение к вычислению поля электрического диполя.

Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке поля равна векторной сумме напряженностей от каждого заряда в отдельности

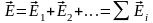
Данное положение называется принципом суперпозиции (наложения) электрических полей, согласно которому напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Электрический диполь – два одинаковых по величине разноименных точечных зарядов, находящихся на расстоянии 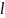друг от друга.

Диполь характеризуется дипольным моментом 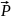- вектор, направленный от отрицательного заряда к положительному и равный произведению заряда 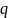на плечо диполя .

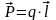
Плечо диполя также является вектором, направленным от отрицательного заряда к положительному, и определяет расстояние между зарядами.

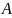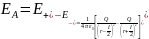Принцип суперпозиции позволяет вычислить величину напряженности поля, создаваемого диполем, например в точке , лежащей на оси. , где 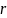– расстояние между средней точкой диполя и точкой , лежащей на оси диполя, в которой определяется напряженность поля.

Билет №2.

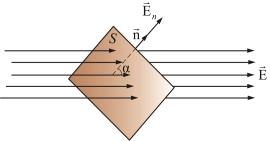
Поток вектора напряженности и его физический смысл.

Полное число силовых линий, проходящих через поверхность S, называется  потоком вектора напряженности 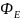    через эту поверхность.

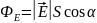, где 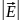 - плотность пронизывания, S – площадка

– скалярное произведение векторов

При одном и том же поле поток вектора напряженности может быть различным. Он максимален, когда 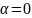и становится равным 0, когда .

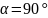Поток вектора Е сквозь произвольную замкнутую поверхность S любой формы:

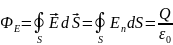
Теорема Остроградского - Гаусса для электрического поля в вакууме.

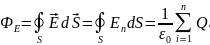
Эта формула является математическим выражением теоремы Гаусса: поток вектора напряженности электрического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме зарядов, которые она охватывает, деленной на ε₀

Применение теоремы Остроградского-Гаусса для расчета электрического поля бесконечной равномерно заряженной плоскости.

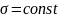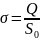
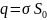
Пусть – поверхностная плотность заряда, находящегося на бесконечной плоскости. Из симметрии ясно, что линии вектора перпендикулярны плоскости и густота их везде одинакова. 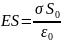. Построим замкнутую поверхность в виде цилиндра, боковая поверхность которого перпендикулярна плоскости. Для обхвата бесконечной плоскости на одинаковых расстояниях слева и справа от плоскости проведем 2 другие плоскости. Т.к. плоскости охватывают бесконечную плоскость, то площадь замкнутой поверхности 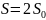. Тогда

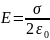
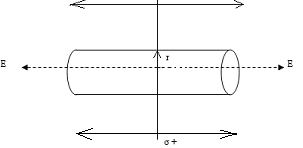
Применение теоремы Остроградского-Гаусса для расчета электрического поля двух бесконечных разноименно заряженных плоскостей.

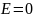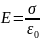Пусть плоскости заряжены равномерно разноименно с поверхностными плотностями . Найдем суперпозицию каждой плоскости отдельно. Слева и справа от плоскостей (линии напряженности направлены друг к другу), а между плоскостями (линии направлены в одну сторону).

Применение теоремы Остроградского-Гаусса для расчета электрического поля равномерно заряженной сферической поверхности.

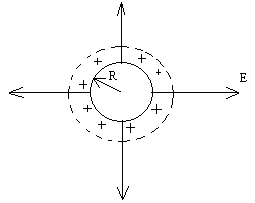
Предположим, что сферическая поверхность радиуса R несет на себе равномерно распределенный заряд q , т.е. поверхностная плотность заряда всюду одинакова σ = const .

Через произвольную точку, находящуюся на расстоянии r > R от центра сферы мысленно построим новую сферическую поверхность S, симметричную заряженной сфере. В соответствии с теоремой Гаусса

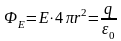.Следовательно, .

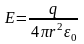Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии можно записать:

Любая замкнутая поверхность, построенная внутри заряженной сферы, не содержит внутри себя электрических зарядов, поэтому Ф_Е согласно теореме Гаусса равен нулю, а следовательно и величина напряженности электрического поля будет равна нулю .

Применение теоремы Остроградского-Гаусса для расчета электрического поля бесконечной равномерно заряженной нити.

– поверхностная плотность заряда  .

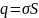
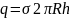
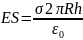1) Начертим замкнутую поверхность в виде бесконечного цилиндра с радиусом r и с центром, совпадающим с центром исследуемого цилиндра.

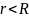
 , т.к. замкнутая поверхность внутри зарядов не содержит

2)  

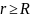
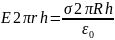
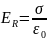
Билет №3.

Потенциал электрического поля.

Отношение потенциальной энергии в величине пробного заряда, помещенного в данную точку пространства

, зависящее от положения пробного заряда, но не зависящее от его численной величины характеризует свойства электрического поля в данной его точке и называется потенциалом этой точки .

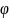Потенциал – скалярная величина, являющаяся энергетической характеристикой электростатического поля.

Когда поле образовано несколькими неподвижными зарядами q₁, q₂, q₃ , …, потенциал его в данной точке равен алгебраической сумме потенциалов ₁, ₂, ₃ , …, создаваемых каждым зарядом в отдельности, т.е. .

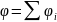Циркуляция электрического поля.

Силы, работа которых не зависит от формы траектории, называются консервативными, следовательно, электростатические силы консервативны.

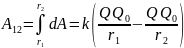Из формулы следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути , равна 0, т.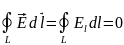е. , где 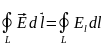- циркуляция вектора напряженности. Если работа не зависит от формы траектории, то она называется потенциальной.

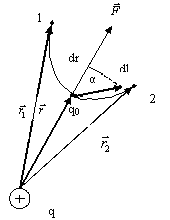
Работа электростатических сил при перемещении точечного заряда.

– работа при перемещении заряда 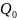из точки 1 в точку 2 не зависит от траектории перемещения ,а определяется только положением начальной и конечной точек. Следовательно, такое эл. поле называется потенциальным, а эл. силы – консервативными.

Потенциальная энергия точечного заряда, системы зарядов.

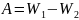
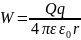– потенциальная энергия точечного заряда.

В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q_i (i = 1, 2, ... ,n). Тогда 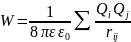- потенциальная энергия системы точечных зарядов.

Потенциал электрического поля и его связь с напряженностью.

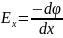Составляющая вектора напряженности электрического поля в данной точке по любому направлению равна производной от потенциала по этому направлению в той же точке, взятой с отрицательным знаком. Из этой дифференциальной формы связи напряженности и потенциала можно получить связь в интегральном виде

.

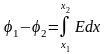В общем виде вектор напряженности электрического поля в данной точке можно представить в зависимости от скоростей изменения потенциала вдоль координатных осей:

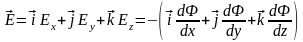
Е = - grad φ,

т.е. напряженность электрического поля в каждой точке равна градиенту потенциала в этой точке.

Эквипотенциальные поверхности.

Для графического изображения распределения потенциала в электростатическом поле пользуются системой так называемых поверхностей равного потенциала или эквипотенциальных поверхностей.

Каждая такая поверхность представляет собой совокупность всех точек поля, имеющих одно и то же значение потенциала .

Линии напряженности в случае точечного заряда всегда перпендикулярны эквипотенциальным поверхностям.

Вычисление разности потенциалов по напряженности поля.

Поле равномерно заряженной бесконечной плоскости задается формулой: , где σ — поверхностная плотность заряда. Разность потенциалов между точками, которые лежат на расстояниях x₁ и х₂ от плоскости, равна (используем формулу ) 

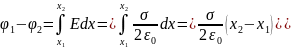
Поле двух бесконечных параллельных разноименно заряженных плоскостей

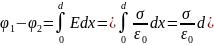
Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы 

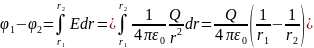
Билет №4.

Диэлектрики в электрическом поле.

Диэлектрик состоит из положительно заряженного ядра и некоторой отрицательно заряженной области, в которой движутся электроны.

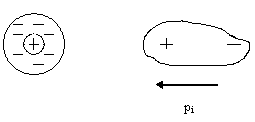
Если «центр инерции» этой области совпадает с ядром, то молекула называется неполярной (H₂, N₂, углеводороды).

Если «центр инерции» области отрицательного заряда не совпадает с ядром, то молекулу называют полярной (H₂O, HCl).

Молекула в этом случае является электрическим диполем с некоторым дипольным моментом 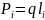, где под q понимается связанный положительный заряд молекулы, а под 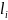- среднее смещение зарядов друг относительно друга.

Типы диэлектриков.

1. Диэлектрик с полярными молекулами – имеют симметричное строение.

2.Диэлектрик с неполярными молекулами – имеют асимметричное строение.

3. Вещества с ионным строением.

Поляризация диэлектриков.

Положительные заряды диэлектрика смещаются по полю, а отрицательные – против поля. Это явление называют поляризацией диэлектрика. В отличие от проводника смещение зарядов в диэлектрике происходит только в пределах каждой молекулы.

В результате поляризации векторная сумма

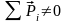
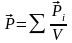- вектор поляризации или поляризованность, где N - число молекул в объеме V.

Виды поляризаций:

1)электронная

2)дипольная

3)ионная

Диэлектрическая восприимчивость, диэлектрическая проницаемость среды.

Эксперименты показывают, что для большинства изотропных диэлектриков (свойства которых по всем направлениям одинаковы) ,

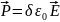где 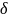– безразмерная постоянная величина, которая характеризует диэлектрик, называется диэлектрической восприимчивостью, .

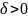Безразмерная величина 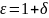называется диэлектрической проницаемостью среды.

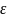показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в эл. поле.

Электрическое смещение.

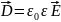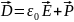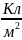- вектор электрического смещения. Можно выразить так: . Единица эл. смещения - . Вектором 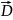описывается электростатическое поле, создаваемое свободными зарядами.

Поток вектора сквозь замкнутую поверхность:

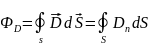
Теорема Гаусса для электрического поля в диэлектрике.

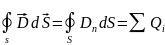поток вектора D сквозь замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью.

Условия на границе раздела двух диэлектрических сред.

Сегнетоэлектрики.

Сегнетоэлектрики – диэлектрики, обладающие в определенном интервале температур спонтанной поляризованностью, т.е. поляризованностью в отсутствие внешнего электрического поля. Сегнетоэлектрик представляет собой как бы мозаику из доменов – областей с различными направлениями поляризованности. Сегнетоэлектрические свойства сильно зависят от температуры, и на определенной температуре они пропадают.