19. Цель статистического анализа временных рядов.

Заключается в изучении соотношений между закономерностью и случайностью, в формировании значений уровня ряда и оценки меры их влияния. Закономерности объясняют динамику показателя в прошлом, используется для прогнозирования его значений в будущем при соблюдении определенных условий, применяемые в обработке ВР методы во многом опираются на методы математической статистики, которые базируются на жестких требованиях к исходным данным:

1. Сопоставимость - достигается в результате одинаково подхода к наблюдениям на разных этапах формирования динамического ряда.

2. Однородность – отсутствие сильных изломов тенденции, а также аномальных наблюдений. Аномальные наблюдения проявляются в виде сильного изменения уровня скачка или спада с последующим восстановлением предыдущего уровня. Наличие аномалий резко искажает результаты моделирования, поэтому аномальные наблюдения необходимо исключать из ВР, заменяя расчетными данными.

3. Устойчивость тенденции – характеризуется преобладанием закономерности над случайностью в изменениях уровни ряда.

4. Полнота данных – обуславливается тем, что закономерность может проявляться лишь при наличии минимально допустимого объема наблюдений.

При исследовании ВР не предоставляется возможности проверить все перечисленные требования, поэтому выводы, полученные на основе статистического инструмента должны дополняться содержательным анализом.

20. Этапы построения прогноза по временным рядам.

Прогнозирование экономических процессов представления ВР сводится к выполнению следующих этапов:

1. Предварительный – анализ данных

2. Построение модели ВР. Выбор аппроксимирующих функций и оценивание параметра модели.

3. Оценка качества модели, проверка их адекватности и оценка точности.

4. Построение точечных и интервальных прогнозов по модели ВР.

21. Предварительный анализ данных.

В ходе этого этапа определяются соответствуют ли имеющиеся данные требованием предъявляемые к ним. Для получения предварительного общего представления о динамике изучаемого показателя во времени целесообразно построить график и провести его анализ. В ходе данного этапа выявляются аномальные наблюдения, проверяется наличие тренда, осуществляется сглаживание ВР, рассчитываются показатели динамики экономических процессов. Для диагностики аномальных наблюдений разрабатываются и применяются различные критерии. Например, метод Ирвина: для всех или только подозреваемых в аномальности наблюдений вычисляется: 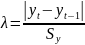, где

, .

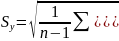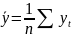Если рассчитанный 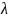превышает табличное значение, то уровень y(t) считается аномальным, его следует заменить расчетным значением, как среднее арифметическое из двух соседних уровней.

Проверка наличия тренда сводится к проверке гипотезы о неизменности среднего значения ВР с помощью различных критериев – критерий серий, основанный на медиане. Все уровни ряда располагаются в порядке возрастания. Определяется выборочная медиана по формуле:

После этого по исходному ВР образуются серии из знаков + и – на статистическом анализе, которого основывается проверка гипотезы о неизменности ВР. Под серией понимается последовательность подряд идущих + и подряд идущих -. Если исследуемый ряд состоит из статистически независимых наблюдений, то чередование последовательностей + и – должны быть случайными. Число серий 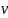(n). Протяженность самой длиной серии Kmax. По паре критериев (n) и Kmax делается вывод: при этом справедлив следующий статистический критерий проверки гипотезы о неизменности среднего значения ВР. Если хотя бы одно из неравенств окажется нарушенным, то гипотеза о неизменности среднего значения ВР отвергается с вероятностью ошибки α и тем самым подтверждает наличие зависящей от времени неслучайной составляющей, а именно тренда. Квадратные скобки выражают тот факт, что результат надо брать в виде целой части от числа.