Пример решения неоднородной слау

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

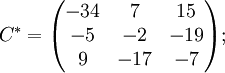
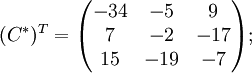
Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

Итак, x=2; y=1; z=4.

23 вопрос: Теорема Кронкера-Копелье. Исследование СЛАУ

24 вопрос:Решение слау методом Гаусса.

25 вопрос: Определители и их свойства.

26 вопрос: Матрицы и действия над ними, обратная матрица, решение матричных уравнений.