Определение

Число называется пределом числовой последовательности , если последовательность является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Частичный предел последовательности — это предел одной из её подпоследовательностей. Верхний предел последовательности — это наибольшая из её предельных точек. Нижний предел последовательности — это наименьшая из её предельных точек.

Обозначения

Тот факт, что последовательность сходится к числу обозначается одним из следующих способов:

• 

• 

Определение. Последовательность называется сходящейся, если у нее существует конечный предел (т.е. существует и ).

Рассмотрим свойства этих последовательностей. 1. Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы ее можно было представить в виде , где , а - б.м.п.

Необходимость. Пусть . Это значит, что

Обозначим . Тогда и

т.е. б.м.п.

Достаточность. Пусть , где а - б.м.п., т.е. .

Но так как , то , т.е. .

Это свойство позволяет почти все остальные свойства свести к свойствам б.м.п.

2. Сходящаяся последовательность ограничена.

Доказательство. , где б.м.п. В силу этого ограничена, т.е. .

Но тогда , т.е. ограничена.

3. Если и сходящиеся последовательности, то тоже сходящаяся последовательность и .

Доказательство:

сходящаяся => , где б.м.п.

сходящаяся=> , где б.м.п.

Но тогда .

Но по свойствам б.м.п. есть б.м.п. и поэтому есть сходящаяся последовательность и 4. Если сходящаяся последовательность, то тоже сходится и

сходится => , где б.м.п.

Но тогда и, по свойству б.м.п. есть тоже б.м.п. Поэтому сходится и 5. Если и сходящиеся последовательности, то тоже сходящаяся последовательность и Доказательство:

сходится=> , где б.м.п.

сходится => , где б.м.п.

Но тогда . Но, по свойствам б.м.п., , , есть б.м.п. их сумма есть также б.м.п. и есть сходящаяся последовательность и . 6. Если , то начиная с некоторого , последовательность ограничена. Доказательство:

сходится => .

Т.к. то возьмем . Тогда

. Но тогда выполняется неравенство

. Сравнивая начало и конец получим, что

и , т.е. при последовательность ограничена. 7. Если и сходящиеся последовательности, причем . Тогда есть также сходящаяся последовательность и

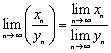
Доказательство:

сходится => , где б.м.п.

сходится => , где б.м.п.

Тогда

.

Вспомним, что . Тогда есть б.м.п., есть б.м.п и, т.к. ограниченна, то есть тоже б.м.п. Итак,

б.м.п. и поэтому

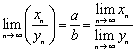
14. Вопрос: Понятие непрерывности отношения к функциям заданным на непрерывном множестве.

Понятие о непрерывности функции.

Вернемся к задаче определения мгновенной скорости в точке (см формулу (1)). Функция

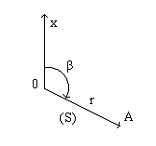
не определена при Δt= 0. Но для числа L = v₀ — gt₀ при уменьшении |Δt| разность v_ср(Δt) - L приближается к нулю. Именно поэтому мы писали v_ср(Δt) → v₀ — gt₀ при Δt→0. Вообще говорят, что функция f стремится к числу L при х, стремящемся к x₀, если разность f(x) - L сколь угодно мала, т. е. |f(x) – L| становится меньше любого фиксированного hɬ при уменьшении |Δх|, где Δх = х—x₀. (Значение х=x₀ не рассматривается, как и в задаче определения мгновенной скорости.)       Вместо х→ x₀ можно, конечно, писать Δх→ 0.       Нахождение числа L по функции f называют предельным переходом. Вы будете иметь дело с предельными переходами в двух следующих основных случаях.       Первый случай — это предельный переход в разностном отношении Δf/Δx, т. е. нахождение производной. С этим пунктом мы познакопились в пункте производная.       Второй случай связан с понятием непрерывности функции. Если f(x) → f (х₀) при х→ x₀, то функцию называют непрерывной в точке х₀. При этом f(x) - L = f (x) - f (х₀) = Δхf; получаем, что |Δf| мало при малых |Δх|, т. е. малым изменениям аргумента в точке х₀ соответствуют малые изменения значений функции. Все известные вам элементарные функции непрерывны в каждой точке своей области определения. Графики таких функций изображаются непрерывными кривыми на каждом промежутке, целиком входящем в область определения. На этом и основан способ построения графиков «по точкам», которым вы все время пользуетесь. Но при этом, строго говоря, надо предварительно выяснить, действительно ли рассматриваемая функция непрерывна. В простейших случаях такое исследование проводят на основании определения 17вопрос: Полярная система координат. Уравнение линии, связь между полярными и декартовыми координатами Полярная система координат Полярная система координат – система плоских координат образованная направленным прямым лучом OX, называющимся полярной осью. Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат - точка O - называется полюсом системы. Положение любой точки в полярной системе определяется двумя координатами: радиусом-вектором r (или полярным расстоянием S) – расстоянием от полюса до точки, и полярным углом b при точке O, образованным осью OX и радиусом вектором точки и отсчитываемым от оси OX по ходу часовой стрелки. Под полярным углом b в геодезии часто принимают дирекционный угол направления, с помощью которого определяют координаты точек и расстояния между ними.

П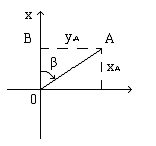 ереход от прямоугольных координат к полярным и обратно для случая, когда начала обеих систем находятся в одной точке и оси OX у них совпадают, выполняется по формулам прямой геодезической задачи:

tgb = Y/X, b = arctg(Y/X)

Эти формулы получаются из решения треугольника OBA по известным соотношениям между сторонами и углами прямоугольного треугольника. Системы прямоугольных и полярных координат применяются в геодезии для определения положения точек на п лоскости.