- •Свойства бесконечно малых функций
- •Связь между бесконечно большой и бесконечно малой функциями
- •Односторонние пределы
- •Общее уравнение плоскости
- •Уравнение плоскости в отрезках
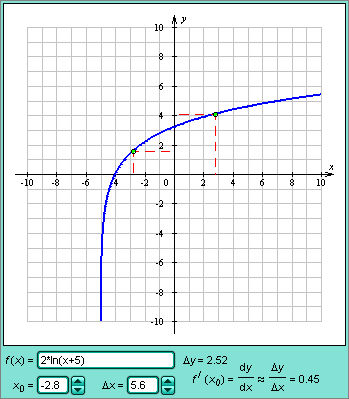
- •Определение производной функции через предел
- •3.1.3. Дифференциал функции
- •Сравнение бесконечно малых функций
- •Первый замечательный предел
- •Определение
- •Обозначения
- •Уравнение линии
- •Общее уравнение прямой линии на плоскости
- •Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному направлению
- •Уравнение прямой, проходящей через две заданные точки
- •Уравнение прямой линии в отрезках на осях
- •Уравнение прямой линии с угловым коэффициентом
- •Связь между декартовыми и полярными координатами
- •Пример решения неоднородной слау
Определение производной функции через предел
Пусть в
некоторой окрестности
точки
![]() определена
функция
определена
функция
![]() Производной
функции
Производной
функции
![]() в
точке
в
точке
![]() называется
предел,
если он существует,
называется
предел,
если он существует,
![]() Общепринятые
обозначения производной функции
Общепринятые
обозначения производной функции
![]() в
точке
в
точке
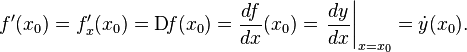 Геометрический
смысл производной. Рассмотрим
график функции y
= f
( x ):
Геометрический
смысл производной. Рассмотрим
график функции y
= f
( x ):
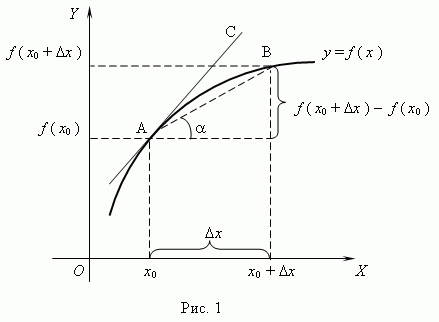
Из рис.1 видно, что для любых двух точек A и B графика функции:
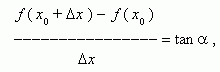
где
![]() -
угол наклона секущей AB.
-
угол наклона секущей AB.
Таким образом,
разностное отношение равно угловому
коэффициенту секущей. Если зафиксировать
точку A и двигать по направлению к ней
точку B, то
![]() неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда следует:
производная функции в точке есть угловой
коэффициент касательной к графику этой
функции в этой точке. В
этом и состоит геометрический
смысл производной.
неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда следует:
производная функции в точке есть угловой
коэффициент касательной к графику этой
функции в этой точке. В
этом и состоит геометрический
смысл производной.
вопрос: Дифференциал функции
3.1.3. Дифференциал функции
Итак,
график дифференцируемой функции в
окрестности каждой своей точки сколь
угодно близко приближается к графику
касательной в силу равенства:
![]() где
α – бесконечно малая в окрестности
где
α – бесконечно малая в окрестности
![]() функция.
Для приближенного вычисления значения
функции f
в точке x0 + Δx
эту бесконечно малую функцию можно
отбросить:
функция.
Для приближенного вычисления значения
функции f
в точке x0 + Δx
эту бесконечно малую функцию можно
отбросить:
|
Линейную функцию
![]() называют
дифференциалом
функции f
в точке
и
обозначают df.
Для функции x
производная в каждой точке
равна 1,
то есть
называют
дифференциалом
функции f
в точке
и
обозначают df.
Для функции x
производная в каждой точке
равна 1,
то есть
![]() Поэтому
пишут:
Поэтому
пишут:
|
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
|
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
|
Модель 3.3. Дифференциал функции. |
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на d
вопрос: Сравнение бесконечно малых функций. Использования эквивалентов бесконечно малых функций При вычислении пределов.
Сравнение бесконечно малых функций
Функция α
(x)
называется бесконечно
малой
при
![]() ,
если
,
если
![]()
Предположим, что α (x) и β (x) - бесконечно малые функции при .
Если
 ,
то говорят, что функция α
(x)
является бесконечно
малой высшего порядка
по сравнению с функцией β
(x);
,
то говорят, что функция α
(x)
является бесконечно
малой высшего порядка
по сравнению с функцией β
(x);
Если
 ,
то говорят, что функции α
(x)
и β (x)
являются бесконечно
малыми одинакового порядка малости;
,
то говорят, что функции α
(x)
и β (x)
являются бесконечно
малыми одинакового порядка малости;
Если
 ,
то говорят, что функция α
(x)
является бесконечно
малой порядка n
относительно функции β
(x);
,
то говорят, что функция α
(x)
является бесконечно
малой порядка n
относительно функции β
(x);
Если
 ,
то говорят, что бесконечно малые функции
α (x)
и β (x)
эквивалентны
при
.
В частности, следующие функции
являются эквивалентными:
,
то говорят, что бесконечно малые функции
α (x)
и β (x)
эквивалентны
при
.
В частности, следующие функции
являются эквивалентными:
|
|
|
|
|
|
|
|
|
|
При вычислении предела отношения двух бесконечно малых функций мы можем заменить эти функции их эквивалентными выражениями.
вопрос: Непрерывность функции в точке. Свойства функций непрерывных на отрезке.
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
![]()
Тот
же факт можно записать иначе:
![]()
СВОЙСТВА
ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
Рассмотрим
некоторые свойства функций непрерывных
на отрезке. Эти свойства приведём без
доказательства.
Функцию y
= f(x) называют
непрерывной
на отрезке
[a,
b],
если она непрерывна во всех внутренних
точках этого отрезка, а на его концах,
т.е. в точках a
и b,
непрерывна соответственно справа и
слева.
Теорема
1. Функция,
непрерывная на отрезке [a,
b],
хотя бы в одной точке этого отрезка
принимает наибольшее значение и хотя
бы в одной – наименьшее.
Теорема
утверждает, что если функция y
= f(x) непрерывна
на отрезке [a,
b],
то найдётся хотя бы одна точка x1
[a,
b]
такая, что з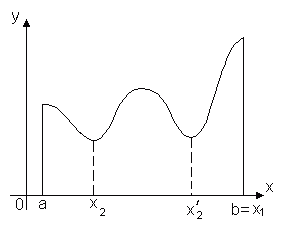 начение
функции f(x)
в этой точке будет самым большим из всех
ее значений на этом отрезке: f(x1)
≥ f(x). Аналогично
найдётся такая точка x2,
в которой значение функции будет самым
маленьким из всех значений на отрезке:
f(x1)
≤ f(x).
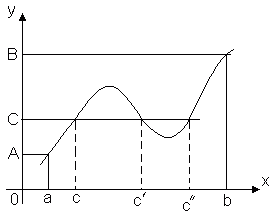
Ясно,
что таких точек может быть и несколько,
например, на рисунке показано, что
функция f(x)
принимает наименьшее значение в двух
точках x2
и x2'.
Замечание.
Утверждение теоремы можно стать неверным,
если рассмотреть значение функции на
интервале (a,
b).
Действительно, если рассмотреть функцию
y = x
на (0, 2), то она непрерывна на этом
интервале, но не достигает в нём ни
наибольшего, ни наименьшего значений:
она достигает этих значений на концах
интервала, но концы не принадлежат нашей
области.
Также теорема перестаёт
быть верной для разрывных функций.
Приведите пример.
Следствие.
Если функция f(x)
непрерывна на [a,
b], то
она ограничена на этом отрезке.
начение
функции f(x)
в этой точке будет самым большим из всех
ее значений на этом отрезке: f(x1)
≥ f(x). Аналогично
найдётся такая точка x2,
в которой значение функции будет самым
маленьким из всех значений на отрезке:
f(x1)
≤ f(x).
Ясно,
что таких точек может быть и несколько,
например, на рисунке показано, что
функция f(x)
принимает наименьшее значение в двух
точках x2
и x2'.
Замечание.
Утверждение теоремы можно стать неверным,
если рассмотреть значение функции на
интервале (a,
b).
Действительно, если рассмотреть функцию
y = x
на (0, 2), то она непрерывна на этом
интервале, но не достигает в нём ни
наибольшего, ни наименьшего значений:
она достигает этих значений на концах
интервала, но концы не принадлежат нашей
области.
Также теорема перестаёт
быть верной для разрывных функций.
Приведите пример.
Следствие.
Если функция f(x)
непрерывна на [a,
b], то
она ограничена на этом отрезке.
Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать. Эта теорема допускает следующее обобщение. Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C. Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C. Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности: Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями. |
|
13 вопрос: Первый замечательный предел