Гидравлический расчет истечения из-под плоских затворов

При гидравлическом расчете истечения из-под плоских затворов различают:

1) свободное истечение, если уровень нижнего бьефа не влияет на величину расхода через отверстие;

2) несвободное или подтопленное истечение, когда уровень нижнего бьефа оказывает влияние на пропускную способность от­верстия.

Истечение будет свободным в следующих случаях:

а) если поток в нижнем бьефе находится в бурном состоянии

i > i_кр и h_б < h_кр ,

где i – положительный уклон дна русла;

i_кр – критический уклон;

h_б – бытовая глубина нижнего бьефа;

h_кр - критическая глубина.

Для русла прямоугольного сечения критическая глубина равна:

, м,

где α – коэффициент Кориолиса. Обычно α = 1,0;

Q – расход воды в канале, м³/с;

g – ускорение свободного падения, м/с²;

В – ширина потока по свободной поверхности, м.

б) если поток в нижнем бьефе в спокойном состоянии

h_б > h_кр ,

и сопряжение бурного потока, вытекающего из-под затвора, проис­ходит в форме отогнанного прыжка (см. рисунок)

h^//_c > h_б

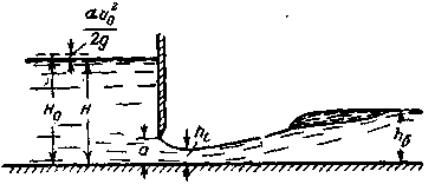
Рис._. 1 – Свободное истечение из-под плоских затворов

или имеет место предельное положение прыжка (прыжок в сжатом сечении)

h^//_c = h_б ,

где h^//_c – вторая сопряженная глубина совершенного гидравлического прыжка, рассчитываемая по формуле:

,

где h_с – глубина в сжатом сечении за плоским затвором, м.

Истечение будет несвободным или подтопленным (см. рисунок 2), ес­ли при спокойном потоке в нижнем бьефе

h_б > h_кр

и сопряжение бур­ного потока, вытекающего из-под затвора, происходит в форме на­двинутого прыжка

h^//_c > h_б

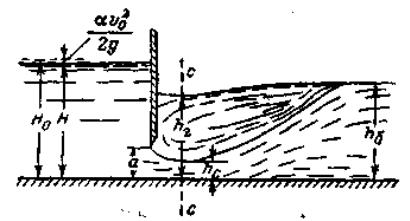
Рис._. 1 – Несвободное (подтопленное) истечение из-под плоских затворов

Условием свободного истечения может служить выражение:

.

Так как щитовые отверстия чаще всего устраивают прямоуголь­ного сечения, то в дальнейшем будем рассматривать истечение из-под плоского затвора только в прямоугольных каналах.

Глубина в сжатом сечении (рис.1) может быть выражена через высоту открытия затвора

, м

- коэффициент вертикального сжатия струи, зависящий для плоского затвора от соотношения а / Н;

- высота открытия затвора, м.

Значения ε, вычисленные по уравнениям Н. Е. Жуковского, приведены в таблице 1.

Таблица 1

	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,45
	0,615	0,618	0,620	0,622	0,625	0,628	0,630	0,638

	0,50	0,55	0,60	0,65	0,70	0,75	-	-
	0,645	0,650	0,660	0,675	0,690	0,705	-	-

При этом имеется в виду, что ширина под­водящего канала равна ширине отверстия, перекрываемого плоским затвором.

Данными табл. 1 можно пользоваться и для расчета отвер­стий с боковым сжатием, так как наличие подводящего канала более широкого, чем отверстие, не оказывает влияния на величину коэффициента вертикального сжатия ε.

Основными расчетными уравнениями при свободном истечений (рис.1) являются:

;

,

где V – скорость в сжатом сечении, м/с;

φ – коэффициент скорости;

μ – коэффициент расхода;

b – ширина отверстия, м;

Н₀ – напор с учетом скорости подхода, м.

Скоростью подхода можно пренебречь, если

м/с

Значения коэффициента скорости φ при истечении из-под пло­ского затвора обычно принимают следующими:

- отверстие без порога: φ = 0,95 - 0,97 (рис. 1);

- отверстие с широким порогом: φ = 0,85 - 0,95.

Расход при подтопленном истечении зависит от величины пере­пада между горизонтом воды перед плоским затвором и в сжатом сечении и определяется по формуле

, м³/с,

где h_z – подтопленная глубина в сжатом сечении с-с (рис.2), в котором пьезометрическое давление минимальное.

μ – коэффициент расхода, который при подтопленном истечении принимается таким же, как при свободном истечении.

Расстояние до сечения с минимальным пьезометрическим дав­лением (сжатое сечение с-с на рис.2) при постоянных относи­тельных открытиях затвора а/Н зависит от относительного подтоп­ления h_б/а.

При h_б = 1,2 а до h_б = 4 а это расстояние изменяется от 0,8а до 2а.

Для практических расчетов это расстоя­ние можно принимать в среднем 1,4 а.

Подтопленная глубина в сжатом сечении h_z при заданном расходе определяется по уравнению

, м

или по уравнению

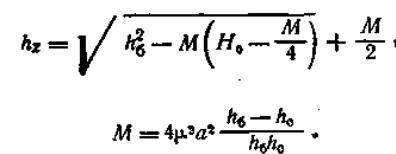
Глубина h_с при подтопленном истечении вычисляется по фор­муле

, м,

причем значения ε принимаются такими же, как при свободном истечении, и берутся из табл.1.

При расчете свободного истечения из-под плоского затвора, расположенного на гребне водослива практического профиля, очер­ченного по форме свободно падающей струи (рис. 3).

Рис.3 - Свободное истечение из-под плоского затвора, расположенного на гребне водослива практического профиля

Расход определяется по формуле

где Н_о - напор над гребнем водослива с учетом скорости подхода;

ε - коэффициент вертикального сжатия, который определяется

по табл. 1.

Формула применима и в случае незатопленного истечения из-под плоского затвора перед перепадом, если сжатие по дну устранено. Коэффициент скорости φ можно ориентировочно принимать следующим:

- при истечении из-под плоского затвора, расположенного на гребне водослива практического профиля, криволинейного очерта­ния, φ = 0,95;

- щитовое отверстие без порога перед перепадом φ = 0,97.

Значения коэффициента расхода (х при различных соотноше­ниях напора к профилирующему напору приведены в курсе гид­равлики ¹.

¹ И. И. Агроскин, Г. Т. Дмитриев, Ф. И. Пикалов, Гидравлика, изд-во «Энергия», 1964, табл. 26-2.