7. Кристаллические решетки. Вектор трансляции. Элементарная ячейка. Примитивная ячейка Вигнера-Зейтца.

Основная особенность кристаллов - периодичность пространственного расположения атомов, молекул или ионов, из которых состоит кристалл, т.е. дальний порядок.

Совокупность таких периодически расположенных частиц образует периодическую структуру - кристаллическую решётку. Точки, в которых расположены атомы - узлы кристаллической решётки.

Представление о пространственной решётке было введено Браве. Периодичность решётки проявляется в так называемой трансляционной симметрии.

Трансляционная симметрия - существуют 3 вектора 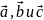, характеризующиесся тем, что при смещении решётки на вектор

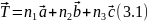-вектор трансляции

где n_1, n₂и n₃ – целые числа (включая 0)

Если выбрать длинны векторов минимальными, но такими, чтобы трансляциями вдоль этих направлений можно было бы получить всю кристаллическую решётку, то эти векторы - основные или базисные вектора, а их совокупность - базис решётки. Началом 3х векторов трансляции можно выбрать любую точку.

Параллелепипед с рёбрами - основной или базисный параллелепипедом. Вместе с находящимися в нём атомами он образует элементарную ячейку кристаллической решётки.

Э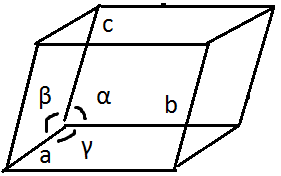 лементарная ячейка в общем виде представляет собой косоугольныйпараллелипипед с рёбрами и углами α(b, c), β(a, c), γ(a, b).

Параметры a, b, c, α, β, γ - параметрами решётки, а a, b , c – постоянные решётки.

Если элементарная ячейка содержит 8 атомов в вершинах основного параллелепипеда, и не содержит ни одного атома внутри объёма или на гранях этого параллелепипеда - примитивной. Все прочие ячейки - сложными.

Возможные различные способы выбора элементарной ячейки. Принято выбирать элементар ячейку так, чтобы она удовлетворяла условиям.:

1. Наилучшим образом отражала симметрию.

1. Имела бы по возможности прямые углы.

2. Обладала бы минимальным объёмом или площадью.

Примитивную ячейку можно получить так:

1. Провести линии, соединяющие выбранную точку со всеми соседними точками.

2. Через середины этих линий провести перпендикуляры.

Полученна ячейка минимального объёма - примитивной ячейкой Вигнера-Зейтца.

8. Решетки Браве. Сингонии. Индексы Миллера.

Решётки Браве

Трансляционные решетки Брове – типы решетки, отличающиеся формами элементарных ячеек и симметрией.

По характеру расположения узлов все элементарные решётки по Браве делятся на 4 типа:

1. Примитивная или Р-ячейка.

1. Базоцентрированная или С-ячейка.

2. Объёмоцентрированная или I-ячейка.

3. Границентрированная или F-ячека.

В кристаллографии для аналитического описания кристаллов пользуются 3-х мерной системой координат, которую выбирают в соответствии с симметрией кристалла. Как правило оси координат совпадают с рёбрами элементарной ячейки, которая характеризуется параметрами a, b, c, α, β, γ. Все кристаллы можно объединить в 7 кристаллографических систем координат или сингоний.

14 трансляционных решёток Бравераспределены по сингониям:

1. Триклинная: имеет примитивную решётку Р

2. Моноклинная: Р, С

3. Ромбическая: Р, С, I, F

4. Тетрагональная: P, I

5. Кубическая: Р, I, F

6. Гексагональная: P

7. Тригональная: Р

Индексы Миллера

Положение плоскости в кристалле можно определить, задав отрезки u, υ и ω, отсекаемой плоскостью на координатных осях. Но в случае плоскостей, проходящей через узлы кристаллической решётки, оказывается более удобным задавать положение плоскости с помощью наименьших целых чисел h, k, l, обратных отрезкам U, υи ω, т.е. выполняется правило:

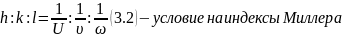
h, k, l называют индексами Миллера. При записи из заключают в скобки: (hkl).