
- •1. Предмет фтт. Основные проблемы фтт.
- •2. Классификация твердых тел. Типы связи.
- •4. Молекулярные кристаллы(мк). Ионные кристаллы(ик).
- •6. Ковалентные кристаллы (кк). Металлы. Плотнейшие упаковки.
- •7. Кристаллические решетки. Вектор трансляции. Элементарная ячейка. Примитивная ячейка Вигнера-Зейтца.
- •8. Решетки Браве. Сингонии. Индексы Миллера.
- •9. Элементы симметрии кристаллов. Точечная группа симметрии. Пространственные группы симметрии.
- •10. Дифракция в кристаллах. Закон Вульфа-Брэгга. Основные дифракционные методы.
- •11. Обратная решетка: свойства, физический смысл.
- •12. Зоны Бриллюэна.
- •13. Классификация дефектов кристаллического строения.
- •14. Точечные дефекты: основные типы, равновесная концентрация, дефекты Шоттки и Френкеля.
- •15. Центры окраски. Радиационные дефекты.
- •16. Краевые дислокации. Винтовые дислокации.
- •17. Контур и вектор Бюргерса. Энергия дислокации. Источники дислокаций.
- •18. Описание энергетического состояния кристалла при помощи газа квазичастиц. Примеры квазичастиц.
- •Адиабатическое приближение Борна-Оппенгеймера.
- •Валентная аппроксимация
- •Одноэлектронное приближение
- •20. Одноэлектронное приближение. Метод Хартри-Фока.
- •V(r) – периодическая функция, период который совпадает с периодом кристаллической решётки.
- •21. Свойства волнового вектора электрона в кристалле. Свободный электрон и электрон в кристалле. Квазиимпульс. Энергетические зоны.
- •2) Рас электрон в кристалле.
- •22. Энергетический спектр электрона в кристалле. Модель Кронига-Пенни. Случаи сильной и слабой связи.
- •23. Заполнение зон электронами. Металлы, диэлектрики, полупроводники.
18. Описание энергетического состояния кристалла при помощи газа квазичастиц. Примеры квазичастиц.
С точки зрения квантовой теории твёрдого тела энергия колебаний решётки (или энергия упругой волны) являются квантовой величиной. Поэтому вводят понятие о фононах - о некоторых, распространяющихся в решётке квазичастицах, обладающих определёнными энергиями и направлениями движения.
Энергия фононов связана с угловой частотой колебаний:

Волновой вектор определяет так называемый квазиимпульс фонона:

Квазиимпульс
- величина, определённая с точностью
до постоянного вектора
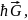 где
–вектор
трансляции обратной решётки. Значение
где
–вектор
трансляции обратной решётки. Значение
 отличающееся на такую величину, физически
эквивалентно.
отличающееся на такую величину, физически
эквивалентно.
Скорость фонона определяется скоростью упругих волн:

Всякое слабо возбуждённое состояние макроскопического тела может рассматриваться в квантовой механике как совокупность элементарных возбуждений. Эти элементарные возбуждения ведут себя как некие квазичастицы, движущиеся в занимаемом телом объёме.
Пока число элементарных возбуждений достаточно мало, они не взаимодействуют друг с другом, так что их совокупность можно рассматривать как идеальный газ квазичастицы. Помимо фононов, существуют и другие важные квазичастицы:
Плазмоны – кванты элементарных возбуждений, обусловленные кулоновским взаимодействием между электронами и положительными ионами. Возникают в металлах и полупроводниках.
Магноны – кванты элементарных спиновых возбуждений; спиновое возбуждение – нарушение спиновой упорядоченности в кристалле. Возникает в ферромагнетиках, антиферромагнетиках, ферримагнетиках.
Экситон – взаимодействие электрона и дырки в кристалле, приводящее к связанному состоянию этих частиц.
Поляроны – электроны, взаимодействующие с фононами; или область искажения решётки вместе с находящимся там электроном.
19. Уравнение Шредингера для твердого тела.
Для твёрдого тела справедливо стационарное УШ, которое описывает состоятие всех частиц в этом твёрдом теле:


где ψ – собственная волновая функция, Е – энергия.
Энергия:


Перейдём к нашему отношению:

Вернёмся к твёрдому тел и запишем оператор кинетической энергии твёрдого тела:

где mi – масса электрона, Mk–масса ядер.
Потенциальная энергия складывается из трёх составляющих:

где r – радиус электронов, R – радиус-вектор ядер, 1-е слагаемое - , 2-е – энергия взаимодействия ядер с ядрами (кулоновское отталкивание ядер), 3-е – энергия взаимодействия электронов с ядрами (кулоновское притяжение электронов и ядер)
Функция ψ, входящее в уравнение Шредингера, зависит от координат всех частиц:

Ряд упрощений для УШ:
Адиабатическое приближение Борна-Оппенгеймера.
Ядра, обладающие большой массой, считаются покоящимися, так как скорость электронов много больше скорости ядер, которые колеблются в узлах решётки. Уравнение Шредингера в этом приближении упрощается: так как ядра покоятся, следовательно их кинетическая энергия равна 0:

Еп – константой

Тогда УШ:

Это уравнение описывает движение электрона в поле покоящихся ядер.
