1.

В курсе строительной механики рассматривается расчет геометрически неизменяемых систем (сооружений), т. е. таких, перемещения отдельных точек которых возможны только в результате деформации систем. Неподвижность таких систем (их геометрическая неизменяемость) относительно земли (под термином «земля» понимается геометрически неизменяемая система-диск), обеспечивается опорными связями (опорами). В опорах возникают реакции, которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на сооружение. Рассмотрим различные типы опор плоских систем: цилиндрическая подвижная или шарнирно-подвижная опора, цилиндрическая неподвижная или шарнирно-неподвижная; защемляющая неподвижная опора или заделка. Как «потребитель» «Строительная механика» опирается, главным образом, на математику, теоретическую механику, сопротивление материалов. В ней используются знания по начертательной геометрии, физике, строительному материаловедению и др.

2.

Стержневыми системами называются системы, состоящие из отдельных, обычно прямолинейных, стержней, соединенных между собой в узлах с помощью сварки, заклепок, болтов или других скреплений, одним из видов таких систем являются плоские фермы.В большинстве случаев соединения стержней фермы в узлах являются жесткими — не шарнирными.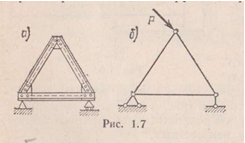

Если заменить жесткие узлы системы, состоящей из трех стержней (изображенной на рис. 1.7, а), шарнирами, то система останется геометрически неизменяемой (рис. 1.7, б), т. е. такой, изменение формы которой возможно лишь в связи с деформациями ее элементов.

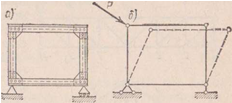
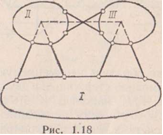
(простейшая геометрически неизменяемая замкнутая система). Если же заменить жесткие узлы шарнирами в системе, состоящей из четырех стержней (изображенной на рис. 1.8, а), то получится система геометрически изменяемая (рис. 1.8, б), т. е. такая, форма которой может меняться без деформации ее элементов.

Систему с двумя стержнями, лежащими на одной прямой (рис. 1.9), в дальнейшем будем называть мгновенно изменяемой, так как она в следующее мгновение после малого смещения точки С по перпендикуляру к прямой АВ превращается в неизменяемую систему.

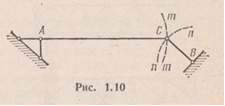
Иная картина получается, если стержни АС и ВС не лежат на одной прямой (рис. 1.10); в этом случае окружности m—m и n-n не имеют общей касательной, а потому даже малое перемещение узла С невозможно без деформации стержней.

Системы, полученные из шарнирного треугольника путем последовательного присоединения узлов, причем каждого двумя стержнями, не лежащими на одной прямой, геометрически неизменяемы, т. е. геометрическая структура их неизменяема. Такие системы (или фермы) называют простейшими в отличие от сложных, которые получают обычно в результате видоизменения простейших, в частности, с помощью замены одних стержней другими, или путем наложения одной системы на другую.

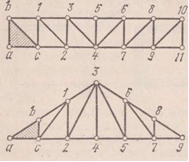
К простейшим системам относятся фермы, представленные на рис. 1.11. Каждая из них получена последовательным присоединением шарнирных узлов указанным выше способом к основному шарнирному треугольнику abc в порядке, обозначенном на чертеже цифрами. В качестве основных треугольников abc при проверке геометрической неизменяемости простейших ферм могут быть приняты любые шарнирные соединения трех стержней.

Ферма, состоящая только из треугольников, геометрически неизменяема. Любой шарнирный треугольник ее может рассматриваться как основной. Проверку геометрической неизменяемости простейших ферм можно производить и обратным путем, т. е. последовательно отбрасывая каждый узел и два стержня, прикрепляющих его к остающейся части фермы. Если в результате этого получится система в виде шарнирного треугольника, то рассматриваемая ферма геометрически неизменяема.

3.

Условие существования геометрически неизменяемой системы является соотношение между количеством стержней и узлов.

Обозначим: S — число стержней фермы, К — число ее узлов. Основной треугольник имеет три узла и три стержня; каждый из остальных присоединяемых узлов в количестве (К—3) прикрепляется двумя стержнями. Поэтому полное число стержней в простейшей геометрически неизменяемой ферме

S=3+2 (К—3),

или

S=2K—3.

Если число стержней S<2K—3, то это показывает, что ферма геометрически изменяемая система или механизм. Примером такой системы может служить четырехугольник (рис. 1.12, а), в котором S=4,K = 4; следовательно,

S=4<2K—3=2*4—3=5.

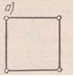
Превращение его в неизменяемую систему может быть достигнуто включением пятого диагонального стержня (рис. 1.12, б).(5=5-статически определимая и геометрически неизменяемая система). Если, далее, введем вторую диагональ — шестой стержень (рис. 1.12, в), то с точки зрения геометрической неизменяемости этот стержень будет уже лишним. Из этого примера видно,что могут встречаться геометрически неизменяемые системы, в которых S>2К—3.

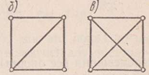
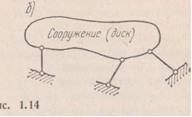
Перейдем теперь к вопросу о присоединении геометрически неизменяемой системы к земле посредством опор. Любую геометрически неизменяемую часть сооружения можно назвать ДИСКОМ. Наиболее часто сооружение (диск) опирается на две шарнирные опоры, одна из которых неподвижная, другая подвижная (рис. 1.14, а). Такая связь сооружения с землей обеспечивает ему геометрическую неизменяемость.

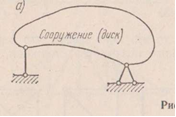
Если все опорные стержни расположены так, что их направления пересекаются в одной точке О (рис. 1.15, а), то эта точка является мгновенным центром, вокруг которого система может совершать бесконечно малое вращательное перемещение (практически это перемещение может быть конечным, но малым).

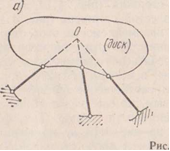
Два диска образуют геометрически неизменяемую систему, если они связаны между собой с помощью трех стержней, оси которых не пересекаются в одной точке и не параллельны друг другу.

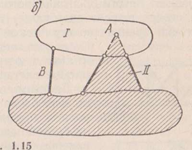
Если направление стержней опорных дисков параллельны или пересекаются в одной точке, система является мгновенно изменяемой.

Систему из трёх дисков можно получить при их соединении шестью стержнями или тремя шарнирами, не лежащими на одной прямой.(система геометрически изменяема).

2 стержня направление которых пересекаются в точке можно заменить шарниром.

4.

Поперечная сила Q положительна, когда на левом торце правой части балки она направлена снизу вверх, а на правом торце левой части — сверху вниз.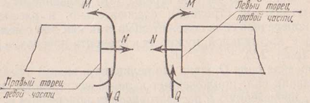

Изгибающий момент М положителен, когда на левом торце правой части балки он направлен по часовой стрелке, а на правом торце левой части — против часовой стрелки. При нагрузках, направленных не по нормали к оси балки (а под другим углом), в поперечных сечениях ее возникают кроме поперечных сил и изгибающих моментов также и продольные силы N. Продольная сила положительна, когда она вызывает растяжение, и отрицательна, когда она вызывает сжатие. Из рисунка видно, что при положительном изгибающем моменте верхние волокна балки испытывают сжатие (укорочение), а нижние — растяжение (удлинение); положительная поперечная сила вращает каждую часть балки относительно другого ее конца по часовой стрелке.При построении эпюр поперечных и продольных сил положительные значения ординат откладывают вверх от оси эпюры, а отрицательные — вниз; полезно указывать на отдельных участках эпюр знаки внутренних усилий. При построении же эпюры изгибающих моментов положительные значения их откладывают вниз от оси эпюры, отрицательные — вверх; в результате этого эпюры изгибающих моментов оказываются расположенными со стороны растянутых волокон балки. При построение этажной схемы балка мысленно рассекается по врезанным шарнирам. На нижних этажах размещаются части балки имеющие опорные подкрепления: либо заделка, либо две вертикальные связи, остальные примыкающие части конструкции располагаются на верхних этажах. Этажная схема: построение эпюр внутренних силовых факторов начинается с балок верхних этажей. На балки нижнего уровня кроме заданных внешних нагрузок с балок верхних этажей передаётся доп. Нагрузка равная реакции в поддерживающем шарнире и взятая с противоположным знаком. Внешняя сосредоточенная нагрузка во врезанных шарнирах распределяется по полам на левую и правую часть конструкции.

5.

Величины опорных реакций, а так же значение внутренних силовых факторов можно определить не только используя метод сечений и построения эпюр, но и при построении и последующим загружением линий влияния. Линией влияния называется график изменения функций какого-либо параметра, возникающего при перемещение по конструкции ед. подвижной нагрузки.

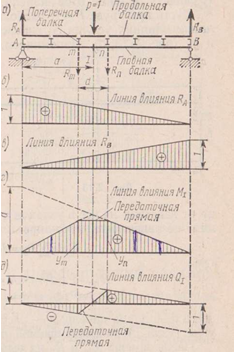
Линию влияния начинаем строить с той части конструкции, которой принадлежит рассматриваемая опора или поперечное сечение. Линия влияния распространяется на соседние балки верхних этажей. При этом ординаты линии влияния в точках расположения реальных опор равна нулю. Если балка имеет консоли то линия влияния консоли распространяется под тем же углом наклона до конца консоли. Линии влияния внутренних силовых факторов. При выводе функций рассматривается два положения нагрузки P=1, а именно слева и справа от сечения, таким образом линия влияния будет иметь две ветви. Переход с левой ветви на правую линию влияния точки силы происходит под сечением. Если балка имеет консоли линии влияния распределяется до конца консоли, при этом левая ветвь линии влияния проецируется на левую консоль, а правая ветвь на правую консоль. Линии влияния распростроняются на соседние балки верхних этажей. При этом ординаты линии влияния в местах установки опор равно 0 и скачков (изменения) ординат быть не должно, возможны только изломы. При этом через балки верхних этажей нагрузки на балки нижних этажей не передаются.

6.

С помощью линии влияния можно вычислить величины тех факторов для которых они были построены, при этом выполняется процедура загружения линии влияния.

1)Действия сосредоточенной силы умножаются на ординаты линии влияния в месте их действия. 2)Равномерно распределенные нагрузки умножаются на площадь линии влияния под зоной их действия. 3)Сосредоточенные моменты умножаются на тангес угла наклона левой ветви в сечении, где действует момент, при этом P и Q считаются положительными, если направлены вниз, M положительны, если направлены по часовой стрелки, а угол наклона альфа отрицательный, если характеризует ниспадающую ветвь.

Невыгодным считается такое положение нагрузки при котором рассматриваемый фактор принимает наибольшее значение. А) Подвижная равномерно-распределенная нагрузка. Невыгодным считается такое расположение нагрузки при котором они располагаются над всей S линии влияния одного знака. Б) Равномерно распределенная нагрузка с заданными разрывами. Величина искомого усилия S зависит от суммарной площади w участков линии влияния под нагрузкой. Невыгодному положению такой нагрузки соответствует условие равенства ординат линии влияния левых и правых площадей. В) Распределение нагрузки над треугольником линии влияния длина которой больше зоны действия распределительной нагрузки. Невыгодное положение нагрузки будет являться условие, когда Yл=Yп.

7.

Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными. Фермы имеют назначение, по существу, такое же, как и балки сплошного сечения, но применяются для перекрытия значительных пролетов, когда проектирование сплошных балок становится экономически невыгодным вследствие неполного использования материала стенки, напряжения в которой меньше, чем в полках. Если ферма получается из шарнирного треугольника последовательным присоединением стержней не лежащих на одной прямой-простейшая.

Классификация ферм по типу нагружения: С ездой поверху, понизу и в середине.

Способ моментной точки. Ферма рассекается на две части так, чтоб в сечение попало не более трёх стержней направление осей которых не пересекается в одной точке, при этом точка пересечения двух стержней относительно которой составляется уравнение моментов называется моментной.

Способ проекций. Способ проекций применяется главным образом в следующих двух вариантах:

1) Рассматривается равновесие части фермы (как и при способе моментной точки), когда два из трёх рассечённых стержней параллельны друг другу;

2) Рассматривается равновесие выделяемых из фермы узлов (способ вырезания узлов).

Если в узле сходятся два взаимно перпендикулярных стержня и нагрузка направлена вдоль одного из них, то усилие в данном стержне равно нагрузке с противоположным знаком, а усилие в перпендикулярном стержне равно 0; Если в узле сходятся три взаимно перпендикулярных стержня и нагрузка направлена вдоль одного из них, то усилие в данном стержне равно нагрузке с противоположным знаком, а усилие в других двух стержнях одинаково.

Передача нагрузки на ферму производится в узлах-шарнирах; следовательно, здесь имеет место случай узловой передачи нагрузки. Поэтому все сказанное в о построении линий влияния при узловой передаче нагрузки на балку относится и к фермам. Аналогично способам определения усилий в фермах при неподвижной нагрузке различаются следующие приемы построения линий влияния для ферм: 1) способ моментной точки, 2) способ проекций.

1. Линии влияния опорных реакций в ферме и в замещающей эквивалентной балки одинаковы.

2. Методика построения линий влияния, усилия в стержнях фермы аналогично методике построения линий влияния в балках при узловой передаче нагрузок.

- если при выводе функции усилия используется метод моментной точки, то пересечение ветвей линии влияния происходит не посредственно под данной моментной точкой.

- в случае полигональных ферм моментная точка может оказаться в негабаритах рассматриваемой конструкции, т.е. точка пересечений ветвей линий влияния может быть за пределами.

Если груз перемещается по узлам нижнего пояса, то верхний узел никогда не будет загружен, усилие в стойке будет =0 и линия влияния будет нулевой.

8.

Арочными называются системы криволинейного или ломаного очертания, в опорах которых от вертикальной нагрузки возникают наклонные реакции, направленные, как правило, внутрь пролета. Горизонтальная составляющая такой наклонной реакции называется распором. Данная конструкция является статически определимая и геометрически не изменяемая. Сооружение с кривой осью, опирающееся на две неподвижные шарнирные опоры (рис. 3.2), носит название двух шарнирной арки.

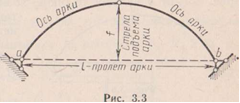
При действии внешней нагрузки на трехшарннрную арку (рис. 3.7, а) в каждой ее опоре возникает по две реакции; всего, таким образом, имеется четыре неизвестные реакции. Вертикальные реакции обозначим через Va и Vb, а горизонтальные — через На и Нв (рис. 3.7, б).

Кроме трех уравнений равновесия, которые дает статика для системы сил, расположенных в одной плоскости, для расчета трехшарнирной арки можно составить четвертое уравнение, основанное на том, что равнодействующая всех сил, приложенных к левой (а также и к правой) половине арки, должна пройти через средний шарнир С, так как в противном случае левая (или правая) половина арки вращалась бы вокруг точки С. Так как момент равнодействующей равен алгебраической сумме моментов составляющих ее сил, то четвертое уравнение статики можно сформулировать следующим образом: алгебраическая сумма моментов сил, действующих на левую или правую половину арки относительно точки С (среднего шарнира), равняется нулю, т. е.

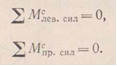
Таким образом, при расчете трехшарнирной арки можно составить следующие четыре уравнения:

(Все силы, действующие на арку, проецируются на ось х); то же, на ось у)

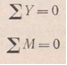
(составляется сумма моментов всех сил, действующих на арку, относительно произвольной точки; удобно в качестве такой точки принимать точку а или в);

Внутренними усилиями являются: изгибающий момент М, поперечная сила Q и продольная сила N, действующие в поперечных сечениях арки. Изгибающий момент, действующий в сечении, равен алгебраической сумме моментов всех внешних левых сил относительно центра тяжести данного сечения или же сумме моментов правых сил, взятой с обратным знаком. Изгибающий момент считается положительным, если левые силы стремятся вращать арку относительно данного сечения по ходу часовой стрелки. Поперечная сила, действующая в сечении, равна алгебраической сумме проекций всех внешних левых сил (или правых сил с обратным знаком) на нормаль к оси бруса в данном сечении. Поперечная сила считается положительной, если сумма проекций левых сил направлена вверх от оси арки. Продольная сила, действующая в сечении, равна алгебраической сумме проекций всех внешних сил (правых сил с обратным знаком) на касательную к оси бруса в данном сечении. Продольную силу считают положительной, если она в сечении арки вызывает сжатие. Изгибающий момент в арки меньше, так как изгибающий момент в арке существенно меньше аналогичного изгибающего момента в балке, то арочные конструкции могут перекрывать существенно больше пролётов в сравнении с балками.

9.

Кроме аналитических методов расчета арок существуют приемы решения этой же задачи, основанные на графических построениях. Рассмотрим случай действия на арку, изображенную на рис. 3.15, а, двух сил Р1 и Р2, приложенных соответственно к левой и правой ее половинам. Определим сначала опорные реакции от действия на арку силы Р1. В этом случае правая опорная реакция В1 должна пройти через правый опорный шарнир и шарнир С (рис. 3.15, а); в противном случае правая часть арки, на которую действуют две силы — опорная реакция В1 и реакция шарнира С, не может находиться в равновесии. На левой опоре арки возникает реакция А1. Таким образом, вся арка в целом будет находиться в равновесии под действием трех сил: А1, В1 и P1.

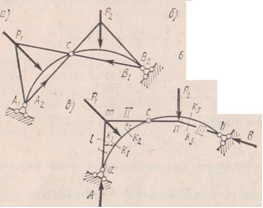
Из курса теоретической механики известно, что три действующие на диск и находящиеся в равновесии силы обязательно пересекаются в одной точке. Если построить векторный многоугольник сил можно определить общие опорные реакции А,В и их направления. Построим верёвочный многоугольник ( рис.3.15,в), соответствующий силовому многоугольнику. Каждый луч верёвочного многоугольника 1,2,3-совпадает с линией давления передаваемого с одной части арки на другую и называется многоугольником давления.

Вдоль линии давления направления равнодействующих сил, действующих на соответствующую часть арки с помощью многоугольника давления можно определить все внутренние силовые факторы, так например момент в сечение Изгибающий момент в сечении k1— k1 равен

где I — плечо, т. е. длина перпендикуляра, опущенного из центра тяжести данного сечения (рис. 3.15, в) на направление равнодействующей левых сил, в данном случае на направление опорной реакции А. При этом очевидно чем меньше плечо, тем меньше величина изгибающего момента, если арки дать очертание при котором её ось совпадает с многоугольником давления, то изгибающие моменты в сечение арки будут равны 0, при этом будут равны 0 и перерезывающие силы, т.е. арка будет работать только на сжатие. Такое очертание оси арки будем называть рациональным.

Рациональным очертанием оси арки, называется такое ее очертание, при котором кривая давления от заданной нагрузки совпадает с осью арки; следовательно, во всех сечениях такой арки изгибающий момент равен нулю. Если ось арки и кривая давления определяются соответственно уравнениями

то условием того, что ось арки имеет рациональное очертание, является тождество Рассмотрим случай действия на арку только вертикальной нагрузки. Составим выражение момента левых сил относительно любой точки с кривой давления:

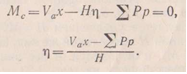Числитель последней формулы численно равен изгибающему моменту в простой балке в сечении с абсциссой Х, т. е. М0х, а потому Используя соотношения , получаем следующее уравнение рациональной оси арки:

Следовательно, при вертикальной нагрузке ось арки будет рациональной, если ее очертание меняется по закону изменения балочного момента.

10.

1) Линии влияния опорных реакций.

Так как опорные реакции в арке и заменяемой балке равны, то и линии влияния Va и Vb будут аналогичны линиям влияния в балках. Распор Н определяется уравнением H=M°с/f.

2) Линии влияния внутренних усилий в сечение арки( n,q,m).

Задача решается методом нулевой точки, при этом нулевыми точками называются точки в которых ординаты линии влияния внутренних сил равны 0.

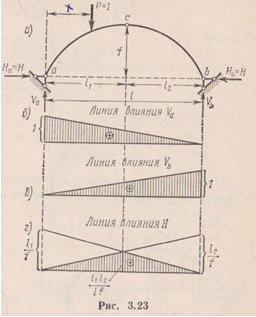
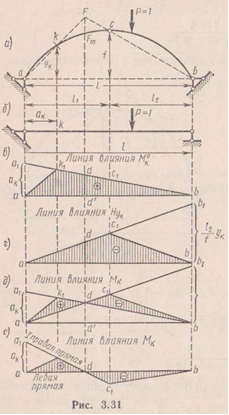
Показанная точка Fm является нулевой точкой для линий влияния изгибающего момента в сечение к.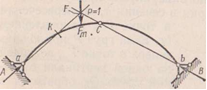

3) Определения положения нулевых точек.

Положение нулевой точки будем характеризовать параметром Q, отсчитываемым от левой опоры арки.

а) Нулевая точка для линии влияния изгибающего момента в сечение к.

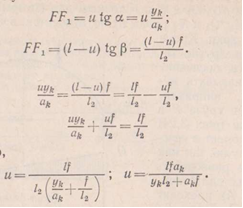
б) Нулевая точка для линии влияния перерезывающей силы.

Так как касательные к оси арки в сечении к параллельно ветви линии давления, то перерезывающая сила в сечении к=0 следовательно точка Fq, в которой находится нагрузка и будет нулевой точкой линии влияния перерезывающей силы в сечении к.

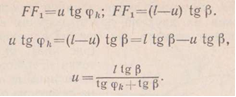
в) Нулевая точка для линии влияния продольной силы.

Касательная к оси арки в сечение к перпендикулярно левой линии давления, поэтому продольная сила в сечение к направлена по касательной к оси арки=0, при этом нулевая точка Fn находится вне габаритах арки.

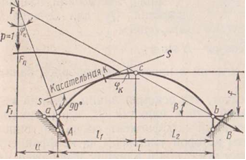
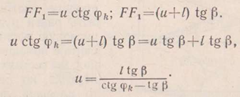
1. Линия влияния изгибающего момента сечения к.

Откладываем над левой опорой величину равную Ак, полученную точку соединяем с нулевой точкой и продлеваем линию до пересечения с проекцией шарнира арки. Построили первую правую ветвь, точка пересечения правой ветви с проекцией шарнира С соединяем с нулём на правой опоре-вторая правая ветвь. Точка пересечения левой и первой правой ветви находятся под сечением к, данную точку соединяем с нулём на левой опоре-левая ветвь.

2. Линия влияния q.

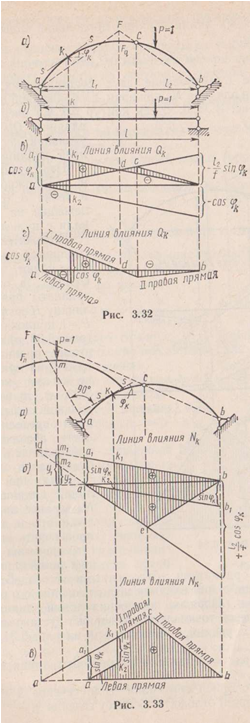
Над левой опорой откладывается ордината равная , полученная точка соединяется с нулём нулевой точке Fq и данная линия продолжается до пересечения с проекцией шарнира С ( построение первой правой ветви), ординату первой правой ветви в шарнире С соединим с нулём на правой опоре следовательно получится вторая правая ветвь. Из нуля на левой опоре проводим линию параллельно первой правой ветви, переход с левой ветви на первую правую происходит непосредственно под рассматриваемом сечение к.

3. Линия влияния продольной силы в сечение арки.

Над левой опорой откладываем величину равную , данную ординату соединяется с нулём в нулевой точке Fn и данная линия продолжается до пересечения с проекцией шарнира С- первая правая ветвь. Ординату первой правой ветви в шарнире С соединим с нулём на правой опоре следовательно получится вторая правая ветвь. Из нуля на левой опоре проводим линию параллельно первой правой ветви, переход с левой ветви на первую правую происходит непосредственно под рассматриваемом сечение к.

11.

Поскольку в сечении арки возникают продольные силы и изгибающие моменты в арке реализуется сложный изгиб или внецентренное растяжение-сжатие. При внецентренном растяжение и сжатии max напряжение в сечениях возникает в наиболее удаленных от центра тяжести волокнах и определяется по формуле

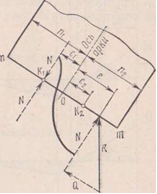
При вычисление напряжения на основе линии влияния необходимо строить и загружать, как линию влияния продольной силы, так и линию влияния момента, что является достаточно трудно-затратной работой.

Данное решение можно упростить. N- продольная сила, приложенная в т. S данного сечения. К-центр тяжести.

Определим напряжение в волокне m-m. Приложим верхнюю ядровую точку К, две взаимно уравновешенных сил

N1=N2=N3=N

Сила N3 проходящая через ядровую точку К, напряжения в волокне n-n не создает, очевидно напряжения в волокне m-m будут вызваны действием изгибающего момента, вызываемого парой сила (N1 и N2). Произведение N (e+C1) представляет собой момент продольной силы, действующей в сечении, относительно верхней ядровой точки называемой ядровым моментом. Ядровый момент отличается от обычного изгибающего момента лишь тем, что при его вычислении приходится умножать левые силы на расстояния не до центра тяжести сечения, а до одной из его ядровых точек.

Таким образом для вычисления максимальных напряжений в сечениях арки нужно построить и загрузить только одну линию влияния ядрового момента. Линия влияния ядровых моментов стоится аналогично линиям влияния изгибающих моментов в сечение арки.

12.

Универсальным методом определения перемещений в упругих системах является метод Мора.

Метод Мора основан на теоремах взаимности работ и перемещений. Перемещения (прогибы и углы поворота) системы в результате ее деформации условимся обозначать Δmn, где индекс m указывает направление перемещения, a n — причину, вызвавшую его. Таким образом, Δmn— перемещение по направлению «силы» m, вызванное «силой» n. Перемещение Δтп может представлять собой либо линейное смещение, либо угол поворота (в радианах) в зависимости от того, является сила m сосредоточенной силой или сосредоточенным моментом. Под силой n понимается любая нагрузка, действующая на сооружение, например нагрузка, состоящая из нескольких сосредоточенных сил и моментов и какой угодно распределенной нагрузки.

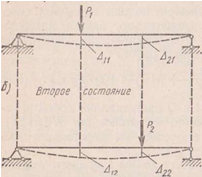
Работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.

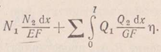
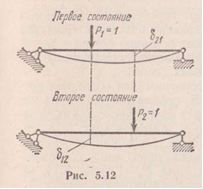
Рассмотрим два состояния системы. В первом состоянии к системе приложена сила Р1= 1, а во втором — сила Р2= 1 (рис. 5.12).Обозначим перемещения, вызванные единичными силами или моментами (т.е. силами Р= 1 или моментами М= 1), знаком δ в отличие от перемещений, вызванных силами и моментами, не равными единице, обозначаемых знаком Δ. В соответствии с этим перемещение рассматриваемой системы по направлению единичной силы Р2 в первом состоянии (т. е. вызванное силой Р1= 1) обозначим δ21, а перемещение по направлению единичной силы Р1 во втором состоянии обозначим δ12 (рис. 5.12). На основании теоремы о взаимности работ для рассматриваемых двух состояний

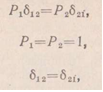или в общем случае действия любых единичных сил

Полученное равенство носит название теоремы о взаимности перемещений (теоремы, или принципа, Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой.

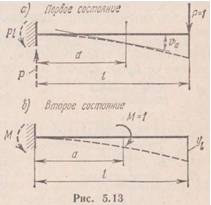
13.

Так как опора статически определимая, то при осадке опор доп. внутренних силовых факторов не возникает, происходит просто кинематическое смещение системы.

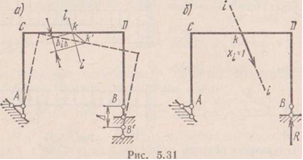
Предположим необходимо определить чему равно перемещение т.К в направлении i-i. Составим новое единичное состояние системы, при этом в исходном недеформированном состоянии в т.К в направлении i-i приложи единичную силу и найдём опорные реакции системы прежде всего реакции смещаемых связей.

Н а основание теоремы о взаимности работ для двух состояний с учётом того, что в первом состоянии внешние силы равны 0, запишем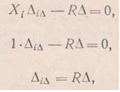

Реакция смещаемой опоры считается положительной если направлена в сторону смещения.

Для определения перемещения, возникающего в статически определимом сооружении от смещения его опор (в направлениях опорных закреплений), необходимо:

1) выбрать единичное состояние сооружения, считая смещающуюся связь неподвижной;

2) загрузить сооружение (в единичном состоянии) в направлении искомого перемещения силой или моментом Xi=1;

3) определить реакции в тех опорных связях единичного состояния, которые в действительном состоянии сооружения смещаются;

4) составить выражение работы сил единичного состояния на перемещениях действительного и приравнять его нулю;

5) решить полученное уравнение относительно искомого перемещения.

14.

Формула Мора может быть представлена в виде:

где —взаимный угол поворота сечений бруса находится на расстоянии dx от действия заданной нагрузки;

взаимное смещение их в направлении оси стержня, находящиеся на расстоянии dx от заданной нагрузки. взаимное смещение поперечных сечений в направление оси y от заданной нагрузки; Δmn- перемещение точки приложение силы Pm=1 от действия заданных нагрузок.

Рассмотрим линейные распределения температур по высоте поперечного сечения стержня. Вследствие изменения температур длина волокон поперечного сечения бруса так же изменяется. Удлинение за счёт нагрева.

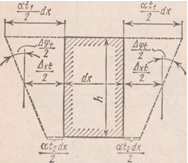
Деформации сдвига в элементе dx от действия температуры не возникают, т. е. Δyn = 0.

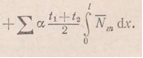
При вычислении перемещения Δmt интегрирование распространяется лишь на те элементы сооружения, температурный режим которых изменился. Для случая прямолинейных или ломаных стержней постоянного сечения интегралы могут быть подсчитаны как площади единичных эпюр, и формула перемещений принимает простой вид:

Здесь - площади единичных эпюр M и N. Знаки членов формулы Δmt определяют так: если деформации элемента dx от температуры и от единичной силы аналогичны, то знак соответствующего члена будет положительным, и наоборот. Сумма производится только по тем элементам конструкции температурный режим которых изменяется.

15.

Определение усилий в статически неопределимой системе связано с необходимостью составления дополнительных уравнений — уравнений деформаций (перемещений) системы. Для этого прежде всего следует превратить заданную n раз статически неопределимую систему в статически определимую, устранив из нее лишние связи. Полученная таким путем статически определимая система называется основной.( Основная система может быть и статически неопределимой).

Устранение каких-либо связей не изменяет внутренних усилий, возникающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе кроме заданной нагрузки приложить реакции устраненных связей, то основная и заданная системы станут эквивалентными.В заданной системе в направлениях имеющихся жестких связей (в том числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в основной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю.Условие равенства нулю перемещения по направлению любой из n отброшенных связей на основании закона независимости действия сил может быть представлено в следующем виде:

Здесь первые индексы означают направление перемещения (и одновременно номер отброшенной связи), а вторые—указывают на причины, вызвавшие перемещение. Таким образом, слагаемое Δik следует читать: “перемещение по направлению связи i, вызванное действием реакции связи k”. Слагаемое Δip означает перемещение по направлению связи i, вызванное действием заданной нагрузки.

Обозначив реакцию связи k (в виде силы или момента) через Хk и выразив перемещения Δik через единичные перемещения с помощью равенства Δik = Xk*δik, представим условие (6.2) так:

(6.3)

Таким образом, условие эквивалентности основной и заданной систем математически сводится к удовлетворению системы n линейных уравнений:

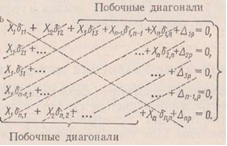
6.4

Уравнения (6.4) являются теми дополнительными уравнениями деформаций (перемещений), которые позволяют раскрыть статическую неопределимость заданной системы. Первое из этих уравнений выражает мысль о равенстве нулю перемещения в основной системе по направлению первой отброшенной связи (по направлению силы или момента X1), второе — по направлению второй отброшенной связи и т. д.

Уравнения (6.4) называются каноническими уравнениями метода сил. Такое название указывает, во-первых, на то, что уравнения составляются по определенному правилу (канону), и, во-вторых, на то, что неизвестными в уравнениях являются силы, представляющие собой реакции отброшенных связей. Число уравнений равно числу отброшенных связей, т. е. степени статической неопределимости заданной системы.

Следует заметить, что вид канонических уравнений, т. е. количество слагаемых в каждом из них и общее число этих уравнений, определяется лишь степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

X1,2,3…-неизвестными являются реакции лишних отброшенных связей.

n- степень статической неопределимости.

Коэффициент δik системы канонических уравнений представляет перемещение по направлению i, вызванное силой, равной единице, действующей по направлению k. Единичные перемещения δii, расположенные на главной диагонали системы канонических уравнений, имеющие два одинаковых индекса, носят наименование главных в отличие от побочных перемещений δik, стоящих вне этой диагонали и имеющих разные индексы. Симметрично расположенные относительно главной диагонали побочные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, а именно:

δik=δki

Для подсчета перемещений рекомендуется вычертить единичные эпюры Mi изгибающих моментов в основной системе (т. е. эпюры от действия Xi= 1), снабдив каждую из них номером соответствующего неизвестного. Отдельно следует вычертить грузовую эпюру (эпюру Мp). Единичное перемещение δik вычисляется умножением единичной эпюры Mi на единичную эпюру Мк, а грузовое перемещение Δip— умножением единичной эпюры Мi на грузовую эпюру Мp.

После вычисления всех единичных перемещений, являющихся коэффициентами при неизвестных в системе канонических уравнений, а также свободных (грузовых) членов этих уравнений, решают уравнения, в результате чего определяют значения неизвестных. Затем строят для основной системы эпюры изгибающих моментов от каждого из найденных усилий, т. е. от Х1,Х2, . . . , Xi . . . , Хn. Для этого могут быть использованы построенные ранее единичные эпюры, все ординаты которых необходимо теперь умножить на найденные значения соответствующих неизвестных.

Окончательная эпюра изгибающих моментов может быть построена и так. К основной системе прикладываются найденные неизвестные усилия и заданная нагрузка, а затем от их суммарного воздействия строится обычными приемами окончательная эпюра изгибающих моментом.

При загружении статически неопределимой системы лишние (основные) неизвестные ( усилия, возникающие в лишних связях) имеют такие значения, при которых потенциальная энергия системы является минимальной. В этом состоит так называемый принцип наименьшей работы. Основной системой метода сил называется статически определимая и геометрически неизменяемая система, которая получается из заданной в результате отбрасывания внешних нагрузок и лишних связей. В основных системах не должно быть замкнутых контуров не связанных с землёй.

Эквивалентной системой называют систему, полученную в результате загружения основной системы внешними силами и реакциями отброшенных лишних связей.

16.

Порядок расчета статически неопределимых систем:

1) выбирается основная статически определимая система путем отбрасывания в заданной системе лишних связей;

2) действие отброшенных связей возмещается приложением к основной системе неизвестных усилий (сил или моментов);

3) составляются канонические уравнения (6.4);

4) основная система поочередно нагружается единичными усилиями X1= 1, Х2=1, . . . , Хn=1 и от каждого из них отдельно строятся единичные эпюры изгибающих моментов Mi. Помимо этого строится грузовая эпюра изгибающих моментов Мр.( Если пренебречь влиянием продольных и поперечных сил нельзя, то аналогично стоятся единичные эпюры Qi и Ni и грузовые эпюры Qp и Np).

5) перемножением единичных эпюр вычисляются все коэффициенты δik системы канонических уравнений;

6) перемножением единичных и грузовой эпюр определяются грузовые члены Δip системы канонических уравнений;

7) решается система канонических уравнений, в результате чего находятся значения неизвестных Х1, Х2, . . . , Хn.

8) для получения окончательной (суммарной) эпюры изгибающих моментов ординаты каждой из единичных эпюр умножаются на найденное значение соответствующего неизвестного и все результаты суммируются (по отдельным точкам осей системы) с добавлением к ним ординат грузовой эпюры моментов. Или же к основной системе прикладываются найденные неизвестные усилия и заданная нагрузка, а затем от их суммарного воздействия строится эпюра изгибающих моментов.

При построении эпюры М ординаты ее отложены со стороны растянутых волокон элементов сооружения, то поперечная сила положительна, если для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится эту ось вращать по часовой стрелке. Вращение оси должно производиться всегда так, чтобы угол поворота не превосходил 90°. Числовое значение поперечной силы равно тангенсу этого угла.

Для определения направления поперечной силы необходимо провести разрез через данное сечение элемента и затем к каждой части такого элемента в разрезе приложить поперечную силу; при этом, если поперечная сила положительна, то она должна вращать каждую такую часть элемента относительно другого его конца по часовой стрелке.

Для построения эпюры N можно вырезать все узлы рамы, приложить к ним действующую на них нагрузку, включая продольные и найденные ранее поперечные силы, и затем составить для этих узлов уравнения равновесия, из которых и определить искомые продольные силы. Для проверки правильности построения эпюр М, Q и N могут быть составлены условия статического равновесия всей рамы или отдельных произвольно выделяемых частей ее (статическая проверка). Например, сумма вертикальных опорных реакций должна уравновесить вертикальную проекцию внешней нагрузки, сумма моментов всех реакций должна уравновесить момент внешней нагрузки относительно любой точки и т. д. Проверка эпюры Q производится также сопоставлением ее с эпюрой М. Так, например, в сечении, где касательная к эпюре М параллельна оси элемента, поперечная сила Q должна равняться нулю; в тех сечениях прямого стержня, где касательная к эпюре М наклонена к его оси в одну и ту же сторону, поперечная сила Q должна иметь одинаковые знаки; из двух сечений элемента то, в котором касательная к эпюре М образует с осью элемента больший угол, имеет и большую поперечную силу и т. д.

Статическая проверка эпюр М, Q и N не может еще гарантировать правильности решения задачи, так как ее условия будут удовлетворяться и при неправильно найденных значениях лишних неизвестных.

Последнее является следствием того, что расчетная эпюра М (для статически неопределимой системы) представляет собой эпюру моментов для основной статически определимой системы от действия на нее заданной внешней нагрузки и найденных лишних неизвестных; поэтому при любых значениях этих неизвестных статическая проверка будет всегда удовлетворяться. Ошибки в найденных значениях неизвестных в большинстве случаев могут быть обнаружены с помощью гак называемой «деформационной проверки», заключающейся в том, что в основной системе определяются перемещения, которые в заданной системе равны нулю или известны.

Можно вывести общее правило, применимое к любой раме. Это правило изложим так: в результате умножения окончательной эпюры изгибающих моментов на любую из единичных эпюр должен получаться нуль или числовая величина заданного перемещения по направлению соответствующего неизвестного (например, при смещении опоры).

Если умножение на каждую единичную эпюру дает нуль (или заданное перемещение ее), то это свидетельствует о правильности окончательной эпюры моментов (при условии, конечно, правильного построения единичных эпюр). Окончательную эпюру можно умножать не только на те единичные эпюры, которые были приняты в расчет, но также на любую единичную эпюру, построенную для статически определимой системы, полученной из заданной отбрасыванием лишних связей.

Это положение основано на том, что всякую статически неопределимую систему (после того как для нее построены эпюры усилий) можно заменить любой (полученной из нее отбрасыванием лишних связей) статически определимой системой, приложив к ней внешнюю нагрузку и реакции отброшенных связей.

Для деформационной проверки могут быть использованы единичные эпюры изгибающих моментов в основной системе, построенные при расчете рамы. Проверка в этом случае сводится к перемножению каждой такой единичной эпюры с окончательной эпюрой моментов. Результат такого перемножения должен равняться нулю.

Но быть уверенным в правильности построения эпюры можно лишь тогда, когда будет сделано столько различных проверок сколько раз система статически неопределима, причем в числе этих проверок не должно быть тождественных. Нельзя, например, подсчитав площади эпюры по двум смежным контурам, затем подсчитать площадь эпюры по суммарному контуру, так как такая проверка будет тождественной с первыми.

17.

Если исходная схема конструкции является геометрически симметричной, то в результате выполнения некоторых процедур можно добиться того, что часть эпюр в системе будут симметричные, часть эпюр обратно симметричные. В соответствии с правилом Верещагина результат перемножения симметричной эпюры на обратно симметричную даёт 0. Таким образом часть коэф. системы уравнений зануляется и решение упрощается, при этом необходимо чтобы основная система так же должна быть геометрически симметричной.