13.1.8.Понятие о множественной корреляции.

Определение: Корреляцию называют множественной, если исследуется связь между несколькими признаками.

В простейшем случае число признаков равно трем и связь между ними линейная: z = ax + by + c.

В этом случае возникают задачи:

1. Найти по данным наблюдений выборочное уравнение связи вида

z = Ax + By + C, (1)

т.е. требуется найти коэффициенты регрессии A и B и параметр C.

2) Оценить тесноту связи между Z и обоими признаками X, Y.

3) Оценить тесноту связи между Z и X (при постоянном Y), между Z и Y (при постоянном X).

Укажем пути решения этих задач:

Задача 1 решается методом наименьших квадратов, причем вместо уравнения (1) уравнение связи удобнее искать в виде:

z - = A (x - ) + B (y - ),

где

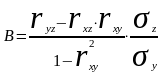
Здесь r_xz , r_yz , r_xy – коэффициенты корреляции соответственно между признаками X и Z, Y и Z, X и Y; σ_x , σ_y , σ_z – средние квадратические отклонения.

Определение: Выборочным совокупным коэффициентом корреляции называется величина R,

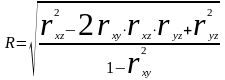
которая оценивает тесноту связи признака Z с признаками X и Y, причем 0 ≤ R ≤ 1.

Определение: Частными выборочными коэффициентами корреляции называются величины

,

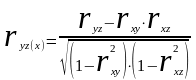которые оценивают тесноту связи между Z и X (при постоянном Y), между Z и Y (при постоянном X) соответственно.

Эти коэффициенты имеют те же свойства и тот же смысл, что и обыкновенный выборочный коэффициент корреляции, т.е. служат для оценки линейной связи между признаками.

13.2.Дисперсионный анализ.

Во многих экономических задачах требуется оценить влияние различных факторов на изучаемую величину X.

Например, разные формы организации производства могут оказывать существенное или несущественное влияние на прибыль фирмы или предприятия.

Другим примером может служить задача оценки эффективности различных видов удобрений. Данный фактор F можно разделить на ряд уровней, в качестве которых могут выступать, например, разные формы организации производства или разные виды удобрений (фактор F – удобрение, а уровни – виды удобрений.).

Суть метода дисперсионного анализа заключается в том, что дисперсия величины X разделяется на две части:

• Факторная дисперсия, вызванная действием фактора F.

• Остаточная дисперсия, обусловленная случайными причинами.

Если выясняется, что факторная дисперсия невелика по сравнению с остаточной дисперсией, то фактор не оказывает существенного влияния на величину X.

Определение: Если рассматривается один фактор, то дисперсионный анализ называется однофакторным, если более одного – многофакторным.

13.2.1.Общая, факторная и остаточная суммы квадратов отклонений

Рассмотрим схему однофакторного дисперсионного анализа.

Пусть на рассматриваемую величину X влияет фактор F, который имеет p уровней. На каждом уровне, т.е. для одного из видов фактора F, проводятся измерения величины X.

Число таких измерений для всех уровней одинаково и равно q. Пусть наблюдалось 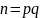значений 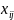признака где – номер измерения; – номер уровня фактора.

Составим таблицу полученных измерений. В последней строке помещены средние значения измерений для каждого уровня:

Номер измерения	F1	F2	…	Fp
1	x11	x12	…	x1p
2	x21	x22	…	x2р
…	…	…	…	…
q	xq1	xq2	…	xqp
Групп.средняя	xгр1	xгр2	…	xгр.р

где F₁, F₂ , …, F_p – уровни фактора,

– общая средняя величина

Определение: Общей суммой квадратов отклонений наблюдаемых значений x_ij от общей средней называется величина:

(1)

Определение: Факторной суммой квадратов отклонений групповых средних от общей средней называется величина:

(2),

которая характеризует рассеяние «между группами».

Определение: Остаточной суммой квадратов отклонений наблюдаемых значений группы от своей групповой средней, называется величина:

(3),

которая характеризует рассеяние «внутри группы».