1.7. Скорость двигателя и ее влияние на динамические свойства электромашинного устройства

1.7.1. Время пуска и торможения [1, 9]

В первом приближении (пренебрегая электромагнитными процессами), динамику ЭП можно описать уравнением движения, из которого определяется время переходных процессов. Учитывая, что в большинстве случаев статический момент во время работы остается практически неизменным, для облегчения условий пуска и останова стремятся обеспечить постоянное ускорение или замедление ЭП в переходных режимах. Это достигается обычно путем поддержания постоянным момента двигателя. Для ДПТ НВ, учитывая связь между механической и электромеханической характеристиками, эта задача сводится, как правило, к поддержанию постоянным тока якоря [1, 2].

Учитывая что в большинстве механизмов , интегрируя уравнение движения, можно определить время переходного процесса:

. (1.21)

Очевидно, что для пуска двигателя из неподвижного состояния до установившейся скорости время пуска будет:

, (1.22)

где - установившееся значение скорости;

- пусковой момент ;

- момент сопротивления.

Точно так же для торможения двигателя до нулевой скорости:

, (1.23) где - тормозной момент;

- скорость до начала торможения.

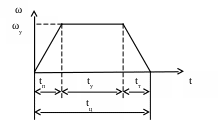
Рис.1.8. Циклограмма режима работы двигателя

В случае пуска двигателя вхолостую

, (1.24)

где =2-3 - кратность пускового момента.

Отсюда видно, что при заданной мощности двигателя продолжительность пуска вхолостую определяется запасаемой в роторе кинетической энергией.

Процессы пуска и торможения являются важными частями циклограммы работы ЭП (рис.1.8).

Циклограмма определяет режим работы двигателя. Если большую часть времени ЭП работает в установившемся режиме, переходные процессы пуска и торможения несущественно влияют на производительность оборудования. В ряде механизмов t_П и t_Т составляют значительную долю цикла и определяют производительность рабочей машины.

Из уравнения движения легко определить длительность переходных процессов в случае линейно изменяющегося момента .

Такой случай имеет место при разгоне двигателя на линейной механической характеристике (рис.1.9):

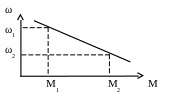
Рис.1.9. Механическая характеристика двигателя

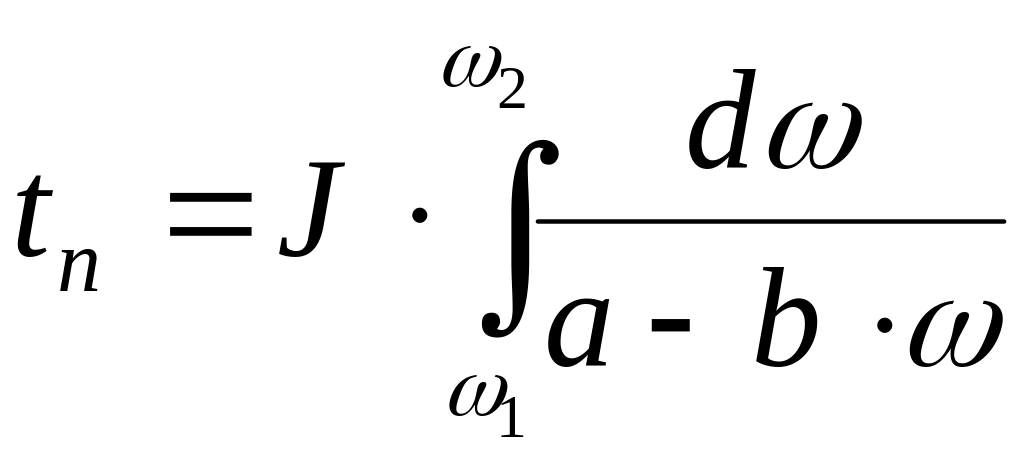. (1.25)

Определим коэффициенты и : для этого запишем уравнение характеристики в следующем виде:

=>

=> .

Следовательно: ;

Интегрируя, получим:

. (1.26)

Полученное выражение позволяет найти длительность любого переходного процесса при линейно изменяющемся динамическом моменте. Отличие состоит лишь в конечных значениях момента и скорости.