2. Электромеханические процессы [1]

Среди механических параметров наибольшее значение для динамики имеет момент инерции вращающихся частей. Моментом инерции тела относительно оси, проходящей через центр тяжести, называется сумма произведений масс элементарных частиц на квадрат расстояния их до этой оси: . В практических расчетах обычно используют . При этом радиусом инерции называется расстояние от оси вращения (проходящей через центр тяжести), на котором надо поместить массу рассматриваемого тела, сосредоточенную в одной точке, чтобы удовлетворялось равенство: .

В большинстве ЭП основная часть момента инерции приходится на долю ротора или якоря двигателя ( ), то есть в первом приближении можно считать, что момент инерции привода примерно равен моменту инерции двигателя. При этом следует иметь в виду, что целый ряд механизмов обладает большими моментами инерции, не учитывать которые нельзя даже в первом приближении. Для более точного расчета переходных процессов необходимо определить моменты инерции рабочей машины и, приводя их к валу ЭД, определить момент инерции всего привода. Если моменты инерции двигателя даются в каталогах, то моменты инерции рабочей машины приходится рассчитывать или определять экспериментально. Для этого часто используют метод выбега.

Момент инерции входит как один из основных параметров при определении электромеханической постоянной времени . Рассмотрим этот процесс.

Момент ЭД при линейной механической характеристике может быть представлен:

, (1.4)

где - момент короткого замыкания, пропорциональный приложенному напряжению;

- крутизна механической характеристики;

 - угловая скорость ротора.

Уравнение движения одномассовой системы может быть записано так:

. (1.5)

Подставим уравнение момента ЭД в уравнение движения, получим:

=> => .

Поделим на с:

=> ,

где - электромеханическая постоянная времени;

- передаточный коэффициент по входному воздействию;

- передаточный коэффициент по возмущающему воздействию.

Учитывая сказанное, в первом приближении электромагнитными процессами пренебрегают и рассматривают ЭП как механическую систему. Такой подход используется часто при анализе приводов переменного тока. Это обусловлено отчасти еще и тем, что описать электромагнитные процессы в приводах переменного тока очень сложно.

1.6. Структурные схемы и передаточные функции элементов электропривода [1, 9]

Поскольку основным элементом ЭП является электрический двигатель, рассмотрим структурную схему и определим передаточную функцию (ПФ) двигателя постоянного тока независимого возбуждения (так как он нашел наибольшее распространение в системах управления).

Будем считать, что , то есть двигатель управляется только по цепи якоря.

При выводе уравнения, описывающего ЭД, пользуются уравнением ЭДС двигателя:

(1.6)

и уравнением движения:

. (1.7)

Первое описывает электромагнитные процессы, а второе - электромеханические. Для удобства уравнения (1.6 и 1.7) запишем в виде:

(1.8)

(1.9)

где I_с – ток, соответствующий нагрузке M_с, а

.

Рассматривая уравнение ЭДС, получим:

, (1.10)

где - электромагнитная постоянная времени цепи якоря.

Если на входе звена мы имеем разность напряжения и ЭДС, то на выходе получим падение напряжения на якоре. Следовательно, уравнение (1.6) можно представить апериодическим звеном.

Умножим уравнение (1.9) на :

. (1.11)

А так как , то, выразив отсюда и подставив в уравнение (1.11), получим:

. (1.12)

Обозначим - электромеханическая постоянная времени.

Из уравнения (1.12) получим:

(1.13)

где - коэффициент, определяемый током статической нагрузки.

Если на входе звена есть разность падения напряжения на якоре от I и от I_С, то на выходе звена получим E, т.о. уравнению (1.13) соответствует интегрирующее звено на структурной схеме. Построим структурную схему двигателя (рис.1.4). Эта схема соответствует работе двигателя в системе управления скоростью, и в том числе в системе стабилизации скорости.

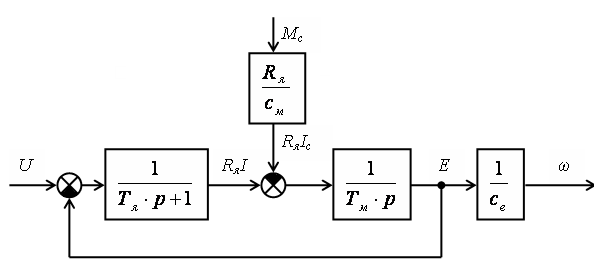
Рис.1.4. Структурная схема двигателя при управлении скоростью

При создании следящих систем нас интересует угол поворота выходного вала .

Так как , то , где - коэффициент передачи редуктора.

Структурная схема двигателя для следящего привода будет выглядеть так (рис.1.5):

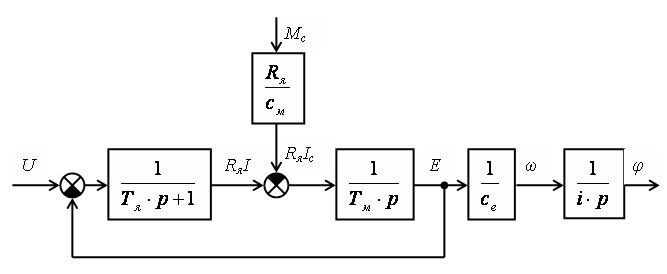
Рис.1.5. Структурная схема двигателя при управлении углом поворота

В результате ПФ по управляющему воздействию при регулировании скорости может быть записана так:

, (1.14)

где - коэффициент передачи двигателя.

В тех случаях, когда на валу двигателя установлен редуктор и нас интересует ПФ исполнительного механизма, записанная по отношению к выходному валу исполнительного механизма, она будет выглядеть так:

,

где .

В следящей системе ПФ двигателя относительно угла поворота:

(1.15)

На практике часто пользуются упрощенной ПФ ДПТ НВ. Учитывая, что электромагнитные процессы протекают значительно быстрее электромеханических, , ими пренебрегают и тогда ПФ двигателя:

, (1.16)

а для следящей системы: . (1.17)

В некоторых случаях для облегчения процедуры синтеза регулятора в системах с подчиненным регулированием координат ПФ двигателя упрощают, пренебрегая ОС по ЭДС. В результате

. (1.18)

Для получения ПФ двигателя по моменту, составим соответствующую структурную схему:

М_С

ω

Рис.1.6. Структурная схема двигателя по возмущающему воздействию

ПФ двигателя по моменту:

, (1.19)

где - коэффициент передачи двигателя.

Теперь рассмотрим асинхронный двигатель.

В машинах переменного тока переходные процессы описываются системой уравнений, в которую входят постоянные времени нескольких взаимосвязанных цепей, поэтому исследование электромагнитных процессов представляет очень сложную задачу. На практике сегодня электромагнитные процессы в машинах переменного тока исследуются обычно в режиме установившейся скорости, что для большинства приводов нехарактерно, поэтому в процессе расчета ЭП чаще всего электромагнитными процессами пренебрегают, учитывая что они быстротечны и заканчиваются в течение одного периода изменения напряжения.

Применительно к трехфазному асинхронному двигателю ПФ в системе управления частотой вращения соответствует апериодическому звену первого порядка:

. (1.20)

При этом постоянную времени приходится определять, линеаризуя соответствующий участок характеристики.

Двухфазные АД, используемые в исполнительных механизмах, работают в широком диапазоне скоростей, начиная от пуска и кончая режимом холостого хода (ХХ).

Рис.1.7. Механические характеристики двухфазного исполнительного асинхронного двигателя

При составлении ПФ также пренебрегают электромагнитными процессами, а постоянную времени определяют, используя момент инерции, скорость ХХ и момент КЗ: , то есть для определения постоянной времени возникает необходимость линеаризации механической характеристики, на которой работает двигатель (рис. 1.7). При такой линеаризации постоянная времени двигателя представляет собой условное время разгона до скорости ХХ без статической нагрузки, при условии, что на валу двигателя действует постоянный момент, равный пусковому ( ). Очевидно, что фактическое время разгона Д будет больше за счет уменьшения момента во время разгона, правда снижение момента ограничено в некоторых случаях кривизной характеристики. Сложность состоит еще в том, что при переходе с одной регулировочной характеристики на другую постоянная времени будет меняться, так как меняется крутизна характеристики, определяемая как . Особенно сильно это сказывается при амплитудном управлении. При фазовом управлении изменение постоянной времени будет существенно меньше, поскольку механические характеристики практически параллельны. Другими словами, двухфазный АД, как и трехфазный, описывается апериодическим звеном первого порядка, но в некоторых случаях, особенно при амплитудном регулировании, следует учитывать изменение постоянной времени .