
- •Определение средней интенсивности трафика. Единица измерения интенсивности трафика.
- •Измерения трафика. Диаграмма Ганта. Нахождение объема пропущенного трафика. Средняя интенсивность трафика.
- •Нормальная оценка интенсивности трафика.
- •4. Диаграмма Кивиата для телефонной линии.
- •5. Как определяется объем трафика и интенсивность трафика?
- •2) Пусть в течение времени т фиксируются длительности ti всех n занятий выходов некоторого пучка, тогда трафик определяют так:
- •6. Программы для мониторинга сетей. Функции и возможности.
- •7. Основные понятия модели потоков событий ( стационарность, последействие, ординарность, интенсивность потока, параметр потока).
- •8 Что такое пуассоновский поток? Перечислите его свойства, параметры.
- •9 Определение примитивного потока
- •20 Примеры самоподобных процессов.
- •21. Основные принципы моделирования потока событий.
- •23. Распределение Вейбулла: математическое ожидание, дисперсия, абсолютные моменты, центральные моменты.
- •24. Самоподобные (фрактальные) модели трафика.
- •25. Поток Эрланга первого, второго и третьего порядка.
- •26. Примеры простейших самоподобных процессов.
- •27. Понятие фрактала. Основное свойство фракталов. Виды фракталов.
- •28. Нормированное фрактальное броуновское движение с параметром Херста.
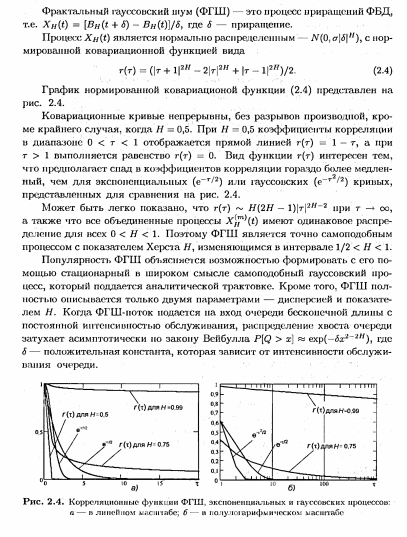
- •29. Фрактальный гауссовский шум.
- •30. Генерирование потока событий с равномерным распределением интервала между событиями.
- •31. Генерирование потока событий, распределенных по закону, отличному от равномерного.
- •32. Модели потоков событий. Метод удачного случайного приращения.
- •33. Модели потоков событий. Метод случайного смещения промежуточных точек
- •34. Модели систем массового обслуживания.
- •35. Задачи анализа и проектирования телекоммуникационных сетей и систем
- •36. Понятие масштабной модели, её назначение и возможности. Анализ недостатков данной модели
- •37. Физическая модель сети типа прототип, её назначение и возможности. Анализ недостатков данной сети.
- •41. Формула Литла для определения среднего числа заявок в системе.
- •45. Смо с полнодоступными и неполнодоступными серверами.
- •47. Анализ механизма приоритетного обслуживания (в лекциях тема 7).
- •46. Анализ работы смо без приоритетов.
- •48. Виды различных дисциплин обслуживания требований.
- •49. Определение среднего времени ожидания в очереди для меченного требования
- •50. Определение консервативной смо. Формула для определения взвешенной суммы времени ожидания в очереди
- •51. Имитационные модели смо, основные задачи построения программы имитации
- •52. Условия, накладываемые на быстродействие алгоритмов имитации
- •68. Непрерывные цепи Маркова.
- •69.Анализ системы «гибели-размножения». Графическая интерпретация процессов переходов в непрерывной цепи Маркова.
- •70. Диаграмма интенсивностей переходов для непрерывной цепи Маркова.
- •71.Уравнения равновесия или баланса.
- •72. Анализ системы массового обслуживания типа m/m/1, диаграмма интенсивностей переходов в этой системе.
- •73 Стационарное распределение вероятностей состояний в системе m/m/1, зависимость среднего времени пребывания в системе в зависимости от коэффициента использования (нагрузки).
- •75. Сравнение характеристик качества обслуживания двухсерверной системы с односерверной.
- •81. Анализ характеристик качества обслуживания системы.
- •85.Модель Энгсета. Схема m-серверной системы с полными потерями
- •86. Диаграмма интенсивностей переходов для m-серверной системы с полными потерями, соответствующей модели Энгсета
- •90 Система с самоподобным входным потоком и детерминированным временем обслуживания
- •91 Расчет основных характеристик системы с самоподобным входным потоком и детерминированным временем обслуживания.
- •92 Анализ телекоммуникационных систем.
- •93. Расчет необходимого числа соединительных линий.
- •95. Анализ сетей массового обслуживания.
- •96 Марковские сети без потерь
- •97 Пример замкнутой сети с тремя узлами. Диаграмма переходов для этой сети.
- •98 Сети с блокировками (потерями). Метод Ли.
- •99. Сравнительный анализ расчетов соединительных линий
- •100 Анализ многозвеньевых коммутационных схем
27. Понятие фрактала. Основное свойство фракталов. Виды фракталов.
Для реального природного фрактала существует некоторый минимальный масштаб длины lmin, такой, что на расстояниях l ≈ lmin, его основное свойство – самоподобие – пропадает. Кроме того, на достаточно больших масштабах длин l > lmах, где lmах – характерный геометрический размер объектов, свойство самоподобия также нарушается. Поэтому свойства природных фракталов рассматриваются лишь на масштабах l, удовлетворяющих соотношению lmin<< l << lmах , в так называемой, промежуточной асимптотике.
Как всякое фундаментальное понятие, фрактал не имеют определения и, следовательно, должен определятся списком свойств.
Тем не менее, существует как минимум три определения фракталов, безусловно, не являющихся полными, каждое из которых обращает внимание на некую существенную особенность этих объектов:
1.фрактал – это объект, в каком-то смысле подобный самому себе;
2. фрактал – это объект, размерность которого строго больше его топологической размерности;
3. фрактал – это объект, содержащий в себе "дыры" всех размеров, что фактически сводится к констатации его самоподобия на разных масштабах.
Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Можно неограниченное количество раз увеличивать ту или иную фигуру, и каждая ее часть будет содержать в себе информацию о всем фрактале.
История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса — самые наглядные, потому что в них сразу видна самоподобность.
В двухмерном случае такие фракталы можно получить, задав некоторую ломаную, называемую генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры (а точнее, при переходе к пределу) получается фрактальная кривая. При видимой сложности полученной кривой, её общий вид задается только формой генератора.
Примерами таких кривых служат:
кривая дракона;
кривая Коха;
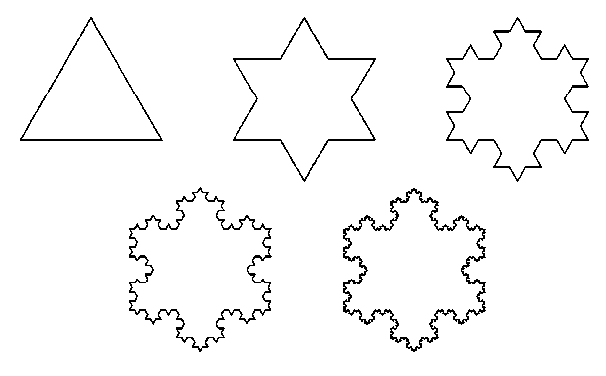
кривая Леви;
кривая Минковского;
кривая Пеано.
К геометрическим фракталам также относят фракталы, получаемые похожими процедурами, например:
множество Кантора;
треугольник Серпиньского;

коврик Серпиньского;
кладбище Серпиньского;
губка Менгера;
дерево Пифагора.
Примеры алгебраических фракталов:
множество Мандельброта;
множество Жюлиа;
бассейны Ньютона;
биоморфы.
28. Нормированное фрактальное броуновское движение с параметром Херста.



29. Фрактальный гауссовский шум.
30. Генерирование потока событий с равномерным распределением интервала между событиями.

31. Генерирование потока событий, распределенных по закону, отличному от равномерного.
32. Модели потоков событий. Метод удачного случайного приращения.
33. Модели потоков событий. Метод случайного смещения промежуточных точек
В отличие от материала, изложенного выше, моделирование процессов фрактального характера еще не стало хорошо изученным предметом и находится в стадии развития. Многие алгоритмы моделирования, опубликованные в последнее время, постоянно совершенствуются. Мы предлагаем здесь несколько базовых подходов, которые представляются нам подходящими для реализации.
Рассмотрим получение последовательности чисел, представляющих случайную реализацию фрактального броуновского движения или фрактального гауссовского шума с заданными параметрами.
Существуют два относительно простых пути генерирования случайной реализации fBM. Это методы, называемые удачным случайным приращением (Successful Random Addition, SRA) и случайным смещением промежуточных точек (Random Midpoint Displacement, RMD). Они обеспечивают весьма точное соответствие сгенерированной последовательности фрактальному броуновскому движению с заданными свойствами. Для получения fGN из fBM достаточно, согласно определению, продифференцировать последний.
Основную идею обоих алгоритмов можно представить с помощью рис. 2.14.
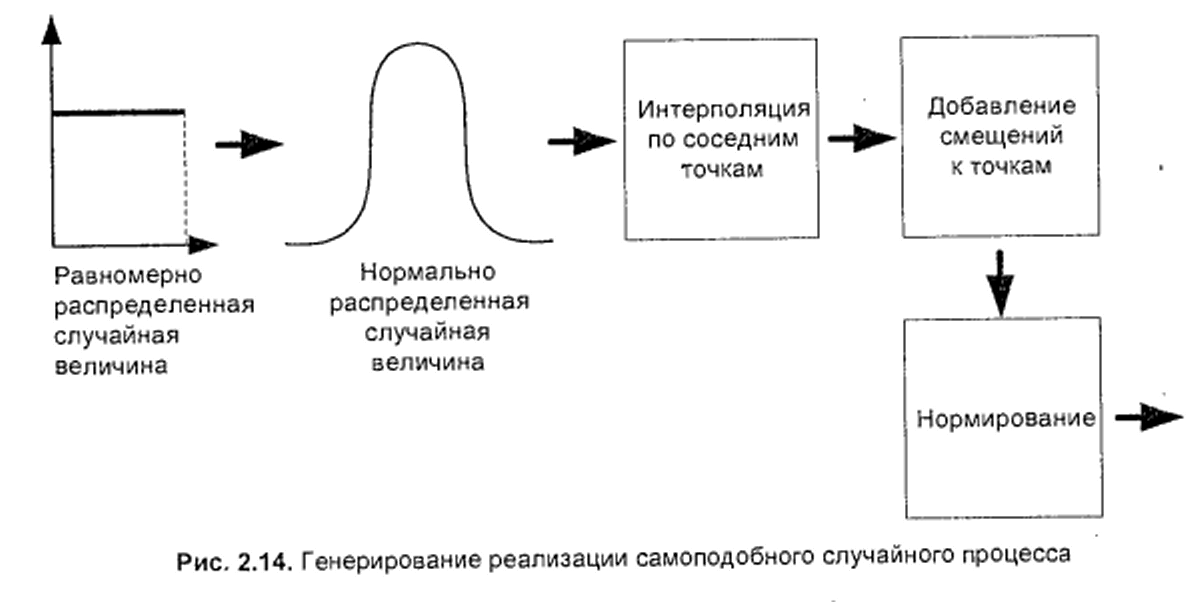
Интерполирование промежуточных точек по двум соседним в данном алгоритме использовано для создания коррелированных нормально распределенных приращений процесса. Добавляя же смещения ко всем точкам реализации, получаем самоподобную нормально распределенную последовательность. Итоговые значения последовательности получаются в результате линейной комбинации нормально распределенных величии. Следовательно, по свойству гауссового распределения результирующие значения также будут распределены нормально.
Пошаговый алгоритм RMD конструирования реализации fBM {X,} на временном интервале (0, 1) с заданной дисперсией σ02 и параметром Херста H выглядит следующим образом:

5/


