8 Что такое пуассоновский поток? Перечислите его свойства, параметры.

Стационарный ординарный поток без последействия называют простейшим. Он задается набором вероятностей P_i(t) поступления i требований в промежутке длиной t.

Можно показать, что при этих предположениях формула для P_i(t) дается формулой Пуассона (Poisson):

.

Одним из важных свойств пуассоновского потока является аддитивность.

Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока _.

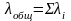П ри разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p_i (p_i =1) поступает на i-тое направление, поток i направления будет также пуассоновским с интенсивностью p _i.

плотность распределения вероятностей у потока: .

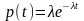Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно

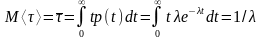
а дисперсия и среднеквадратическое отклонение соответственно будут равны:

,

.

9 Определение примитивного потока

Это ординарный поток, параметр которого прямо пропорциона­лен числу свободных источников N_i =(N-i). Здесь N – общее число источников требований, i- число обслуживаемых в данный момент источников. Для примитивного потока параметр потока определяется как λ_i=αN_i=α(N-i) с некоторым коэффициентом α. Среднее значе­ние параметра примитивного потока: 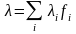, где f_­i - вероятность того, что об­служивается i источников. Средняя интенсивность потока заявок от одного источника: .

10. Потоки событий с произвольным законом распределения

Потоком с произвольным законом распределения называют распределение случайной величины, которая описывает интервал времени между поступлениями событий. Распределения бывают следующими:

11. Равномерное распределение. Плотность распределения, функция распределения, математическое ожидание, дисперсия.

12.Треугольное распределение: функция плотности вероятности, функция распределения, математическое ожидание, дисперсия.

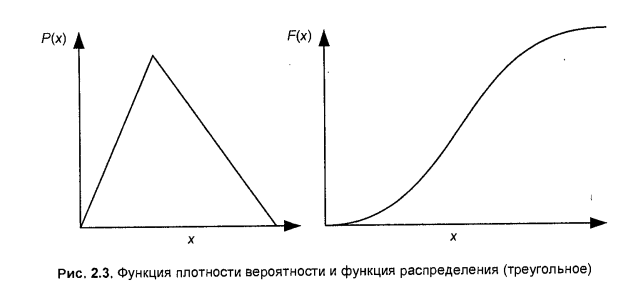
Дисперсия

13. Нормальное распределение. Стандартное нормальное распределение. Функция Лапласа.

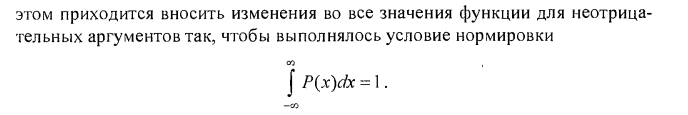
14. Логнормальное распределение. Плотность распределения, функция распределения, математическое ожидание, дисперсия.

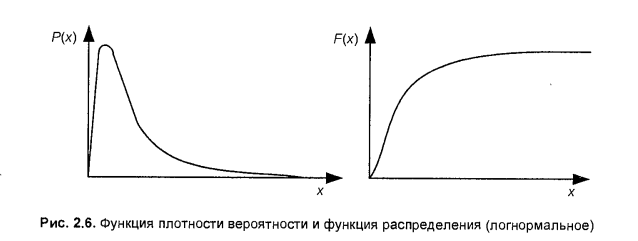
15 Распределение - квадрат: математическое ожидание, дисперсия.

16 Распределение Стьюдента: математическое ожидание, дисперсия.

17 Распределение Фишера: математическое ожидание, дисперсия.

18 Потоки с ограниченным последействием. Поток Пальма.

Ординарный поток событий называется потоком с ограниченным последействием (потоком Пальма), если промежутки времени между соседними событиями  ,  ,… представляют собой независимые СВ.

Очевидно, простейший поток является частным случаем потока Пальма. Обычно потоки Пальма получаются в виде выходных процессов систем распределения информации.

Основной в теории выходных потоков является теорема Пальма, которая звучит следующим образом. Пусть на систему распределения информации поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ. Если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок является потоком типа Пальма.

В частности, если входной поток заявок будет простейшим, то поток необслуженных, не будучи простейшим, будет все же иметь ограниченное последействие.

Рассмотрим один из типов потоков с ограниченным последействием, потоки Эрланга. Они образуются «просеиванием» простейшего потока. Если, например, из простейшего потока выбросить каждую вторую точку, то оставшиеся точки образуют поток Эрланга 1-го порядка. В то же время этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то независимы и величины  ,  ,…, получающиеся суммированием таких промежутков по два.

В общем случае, потоком Эрланга  -го порядка называется поток, получаемый из простейшего, если сохранить в нем каждую   точку, а оставшиеся выбросить.

Найдем закон распределения промежутка времени   между соседними событиями в потоке Эрланга  -го порядка. Рассмотрим на оси   простейший поток с интервалами  ,  ,… (рис. 1.5).

Рис. 1.5. Расположение заявок в простейшем потоке

Величина   представляет собой сумму   независимых СВ:

,

где   - независимая СВ, подчиненная экспоненциальному закону распределения

,  .

Обозначим через   ПРВ величины   для потока  . Вероятность того, что СВ   попадет в интервал  , равна  . Это значит, что последняя точка промежутка должна попасть на данный элементарный участок, а предыдущие   точек на участок  . Вероятность первого события равна  ; вероятность второго

,  .

Перемножая данные вероятности, получим следующий закон распределения величины  :

,  ,

откуда

,  .

Математическое ожидание потока   определяется выражением

,

где   - математическое ожидание промежутка между соседними событиями в простейшем потоке. Дисперсия потока Эрланга  -го порядка определяется по формуле

;  .

19 Параметр Херста для самоподобных процессов с долгосрочной зависимостью.

Важнейшим параметром, характеризующим «степень» самоподобия СП, является параметр Хёрста.

Для выборочного случайного набора   можно определить выборочное среднее

,                                                                  (5.10)

выборочную дисперсию

                                                    (5.11)

и интегральное отклонение

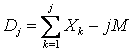.                                                            (5.12)

Определим изменчивость СП на интервале   как неубывающую функцию длины интервала

.                                                 (5.13)

Хёрстом было показано, что для большинства естественных процессов при больших значениях   выполняется соотношение

или иначе

.                                                   (5.14)

Величина   получила название параметра Хёрста и лежит в интервале  . Для процессов, не обладающих свойством самоподобия,  0.5. Для самоподобных процессов с долгосрочной зависимостью этот параметр изменяется в пределах 0.7…0.9. Параметр  , который был введен выше для задания асимптотических свойств характеристик самоподобных СП, может быть выражен через параметр Хёрста:

.