99. Сравнительный анализ расчетов соединительных линий

p . вероятность потерь, a ω_i . вероятность занятости каждой дуги i-ro звена

Обозначим вероятность занятости дуг для параллельно-последовательного графа, приведенного на рис. 9.11a, соответственно ω₁ (для дуг Aαι), ω₂ (для дуг α_iβ) и ω₃ (для дуги βB), а вероятности свободности этих же дуг через q₁=1.ω₁, q₁=1.ω₂ и q₃=1.ω₃. Тогда вероятность того, что один из путей между полюсом А и вершиной β, состоящий из двух дуг, будет свободен, составит вероятность занятости этого пути

Вероятность занятости всех т₁ путей между полюсом А и вершиной р будет равна

Для того чтобы подсчитать вероятность потерь р, равную вероятности занятости всех

123 возможных путей между полюсами А и В (ω_AB) , определим вероятность свободности хотя бы одного пути между полюсами А и В как произведение вероятностей свободности ветви Aβ и дуги βB:

В свою очередь, вероятность потерь будет равна

100 Анализ многозвеньевых коммутационных схем

Помимо двухзвеньевых коммутационных схем в коммутационной технике широко применяются многозвеньевые схемы. В частности, квазиэлектронные системы коммутации используют четыре - восемь звеньев соединения.

На рис. 9.4 приведена трехзвеньевая схема, показанная в двух вариантах.

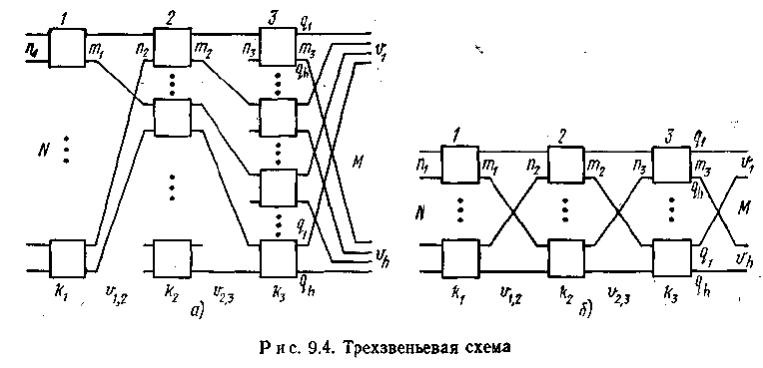
Если в схеме между любым из входов и любым коммутатором последнего звена имеется не более одного соединительного пути, то такую структуру называют веерной (рис. 9.4а); если число соединительных путей более одного, структуру называют связанной (рис. 9.4б). Обозначения структурных параметров для трехзвеньёвой схемы, приведенной на рис. 9.4, аналогичны обозначениям параметров двухзвеньевой схемы. Трехзвеньевая схема помимо режима группового искания может быть использована и в режиме индивидуального искания (кроме веерной, так как она имеет не более одного пути между заданным входом и требуемым выходом). В этом случае в каждом направлении имеется лишь один выход.

На рис. 9.5а приведена четырехзвеньевая коммутационная схема с неделимой структурой, т. е. со структурой, которая не распадается на блоки, а на рис. 9.5б . четырехзвеньевая схема блочной структуры. При блочном построении коммутаторы первого и второго звеньев, а также третьего и четвертого звеньев соединяются таким образом, что представляют собой отдельные двухзвеньевые блоки. Несколько таких блоков образует левую группу, находящуюся в первых двух звеньях. Аналогичное построение имеет и правая группа (третье и четвертое звенья). Левые и правые двухзвеньевые блоки связаны между собой. Схему, приведенную на рис. 9.5б, иногда называют итерационной схемой, так как ее можно получить, заменяя каждый коммутатор двухзвеньевой схемы такой же двухзвеньевой схемой. На этом рисунке число коммутаторов в каждом звене обозначено k₁,...,k₄, a число коммутаторов в каждом блоке соответствующего звена обозначено l₁,...,l₄. Для построения коммутационных схем с большим числом звеньев могут быть использованы те же закономерности структуры, которые показаны на примерах двух.четырехзвеньевых схем. Так, например, восьмизвеньевая схема может быть построена из нескольких четырехзвеньевых схем (см. рис. 9.5), соединенных между собой в одну общую схему.

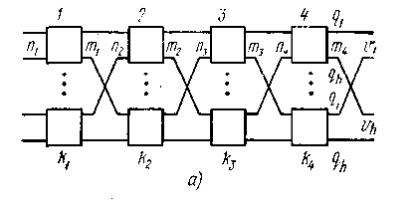
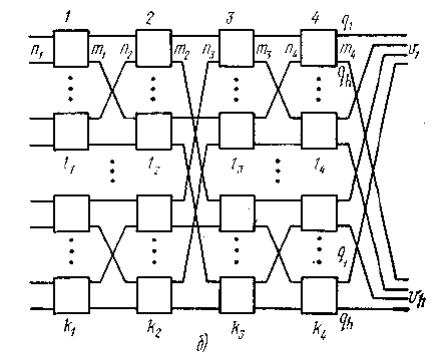
Рис. 9.5. Четырехзвеньевая схема

На основе рассмотренных схем легко представить себе построение схем с числом звеньев более восьми.

Существенную роль в коммутационных схемах играет отношение числа выходов к числу входов на каждом звене, которое называется коэффициентом расширения, если это отношение больше единицы, или коэффициентом концентрации, если оно меньше единицы. Для трехзвеньевой схемы, приведенной на рис. 9.4, таким образом, можно рассматривать три коэффициента: σ₁=σ_вх=υ_1,2/N; σ₂=υ_2,3/υ₁,₂; σ₃=σ_вых=M/υ_2,3. В схемах с любым числом звеньев количество коэффициентов а равно числу звеньев.

В режиме группового искания, когда заданный вход схемы должен быть подключен к любому свободному выходу требуемого направления, схемы, как правило, должны иметь расширение. Особо существенную роль играют коэффициенты σ_вх и σ_вых, относящиеся к первому и последнему звеньям.

Мостиковый граф

Мостиковый граф – граф, относящийся к классу непараллельно- последовательных графов

Приведенные на рис. 9.11 три вероятностных графа трехзвеньевой схемы рис. 9.4б соответствуют, как указано выше, трем режимам искания. В режиме И трехзвеньевая схема имеет граф параллельно-последовательного типа (тип П), а в режимах Г и С - граф непараллельно-последовательного типа (тип Н).

Метод оценочных графов

В тех случаях, когда вычисление потерь для непараллельно-последовательного графа слишком громоздко, можно пользоваться методом оценочных графов.

Для рассматриваемого графа из класса непараллельно-последовательных схем подбирают два параллельно-последовательных графа, причем таким образом, чтобы вероятность потерь для одного из них была оценкой сверху вероятности потерь в рассматриваемом графе, вероятность потерь для другого графа . оценкой снизу. Тогда искомая вероятность потерь для исследуемого графа будет заключена между двумя значениями потерь, выражения для которых легко записать.

Получение оценочных графов осуществляется с помощью некоторых операций. Граф для получения оценки по потерям сверху получают путем использования операций выбрасывания отдельных дуг и разделения одной вершины на две или несколько, что приводит к заведомому увеличению потерь. Для получения графа, пригодного для оценки вероятности потерь снизу, используются противоположные операции добавления дуг и объединения вершин, которые приводят к уменьшению потерь.