97 Пример замкнутой сети с тремя узлами. Диаграмма переходов для этой сети.

Определим систему уравнений локального равновесия как систему, в которой приравнивается интенсивность потока из данного состояния сети за счет ухода заявок из узла i к интенсивности потока в данное состояние сети за счет поступления требований в узел i .

Покажем это на примере:

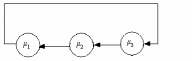
Рис. 1.29 Замкнутая сеть с тремя узлами.

Пусть в замкнутой сети с тремя (N=3) узлами циркулирует ровно два требования (K=2).

Состояние сети описывается тройками: .

Всего в сети возможно различных состояний .

На рис. 1.30 показана диаграмма интенсивностей переходов между этими состояниями.

Рис. 1.30 Диаграмма интенсивностей переходов для замкнутой сети с тремя узлами.

Если записать систему уравнений глобального равновесия, то она будет состоять из шести уравнений, одно из которых обычно избыточно из-за существования условия нормировки.

В каждом из этих уравнений левая сторона соответствует потоку исходящему из данного состояния, а правая – потоку, входящему в это состояние.

С точки зрения локального равновесия первые три уравнения именно такими и являются. В остальных уравнениях видно, что первое слагаемое правой части уравновешивается первым слагаемым левой части. И также для вторых слагаемых.

Следовательно, уравнения локального равновесия могут быть выписаны так

Первое из этих уравнений описывает локальный баланс для узла 1, а второе – для узла 2. Вместе всего образуется девять уравнений локального равновесия, из которых четыре – избыточны. Решение дается следующими формулами

Как видно, решение уравнений локального равновесия отыскать значительно проще. В любом случае поиск стационарных вероятностей сводится к решению больших систем линейных уравнений. Заметим еще раз, что рассмотренные сети массового обслуживания удовлетворяли требованиям эргодической марковской цепи.

98 Сети с блокировками (потерями). Метод Ли.

Марковский подход к анализу сетей массового обслуживания позволяет рассчитать вероятности состояний для сетей, состоящих из узлов, каждый из которых есть СМО типа M/M/m. При этом предполагается, что каждый узел содержит бесконечный накопитель, и все заявки будут обслужены через некоторое время. Другой постановкой задачи является анализ сети с узлами, в которых может быть СМО с блокировкой заявок. Часто такими СМО выступают коммутационные схемы, имеющие конечные пучки соединительных линий. Другой моделью являются сети с множественным доступом к фиксированному числу каналов. Рассмотрим в качестве примера (рис.1.31) подключение сельского абонента С через абонентскую линию с блокиратором к сельской АТС в пункте В, которая в свою очередь имеет два канала связи с АТС в пункте А. Требуется определить вероятность блокировки звонка абоненту С из пункта А. Поставим в соответствие рассматриваемой сети так называемый вероятностный граф (граф Ли), с вершинами А, В и С и ребрами a,b,c соответствующими потокам заявок. Будем называть их далее звеньями, и параметризовать значениями некоторых вероятностей их занятия.

Рис. 1.31 Подключение абонента С с абонентом А через АТС в пункте В.

Метод Ли состоит в том, что вероятность блокировки пути между любыми вершинами графа может быть рассчитана как вероятность совместного занятия всех соединяющих эти вершины звеньев в предположении, что вероятности занятия каждого из звеньев независимы.

Вероятность совместного занятия может быть рассчитана с помощью известных теорем теории вероятностей для сложных событий.

Обозначим вероятности занятия звеньев a,b,c соответственно .

Вероятности того, что звено свободно можно найти как

.

Вероятность блокировки пути АВ будет определяться как совместная вероятность занятости a и b: .

Вероятность свободности этого пути: .

Общая вероятность свободности пути АС будет

.

Тогда вероятность блокировки пути АС будет

.

Граф, рассмотренный здесь, относится к классу параллельно-последовательных. Для расчета вероятностей таких графов в общем случае применяются простые правила, сведенные ниже в таблицу:

Вероятность занятости (блокировки)	wi=1-qi
Вероятность свободности (неблокированности)	qi=1-wi
Параллельное включение звеньев	w=w1w2w i…wn
Последовательное включение звеньев	q=q1q2qi…qn

Бывают случаи, когда граф сети не сводится к параллельно-последовательным схемам. Например, мостиковый граф (рис. 1.32)

Рис. 1.32 Мостиковый граф.

Для такого графа можно получить вероятность блокировки пути АВ в виде

.

Графы типа приведенных выше часто встречаются при анализе многозвенных коммутационных схем. Там они имеют более сложный вид, например как на рис. 1.33 и 1.34.

Рис. 1.33 Пример параллельно – последовательного графа.

Рис. 1.34 Пример параллельно – последовательного графа.

Для этих графов можно получить явные выражения для вероятности блокировки пути АВ

В том случае, если граф получается слишком сложным, можно пользоваться методом оценочных графов. Строится граф оценки сверху путем разделения вершин и отбрасывания ребер для упрощения расчета и граф оценки снизу путем объединения части вершин. Рассчитываются вероятности блокировки для оценочных графов, которые и будут служить соответственно верхней и нижней границей, между которыми и будет лежать значение вероятности блокировки для исходного графа.