90 Система с самоподобным входным потоком и детерминированным временем обслуживания

91 Расчет основных характеристик системы с самоподобным входным потоком и детерминированным временем обслуживания.

Допустим, что имеется цифровая система, состоящая из буфера и одного сервера с постоянной интенсивностью обслуживания   пакетов/сек (рис. 6.4).

Рис. 6.4. Схема односерверной цифровой системы

Будем полагать, что входной цифровой поток описывается ФБД с интенсивностью  . В работе Норроса [5] было показано, что число поступивших пакетов за время   определяется величиной

,

где   - масштабный коэффициент;   - нормированное ФБД с параметром Херста  . Норросом было показано, что вероятность того, что количество пакетов   в системе превысит заданную величину  , определяется выражением

,

где 

- дополнительная функция распределения стандартного гауссовского распределения. Представленное выражение можно интерпретировать как вероятность блокировки пакета при ограниченном объеме буфера   пакетов.Если задать необходимую величину   вероятности блокировки пакета в системе, т.е.  , то из последнего выражения можно получить формулу для расчета величины буфера:

,

где   - величина входной нагрузки. Выражая величину   (объем буфера), получаем

.

Используя формулу Литтла, можно определить среднее время пребывания пакета в системе

.

Неожиданным результатом для исследователей стал тот факт, что время обработки превысило даже оценку, полученную в предположении экспоненциального закона распределения времени поступления заявок и времени их обработки, т.е. системы типа М/М/1. Ранее считалось, что система М/М/1 дает самую завышенную оценку для времени пребывания, по сравнению со всеми другими способами оценивания.Таким образом, системы с самоподобным трафиком приводят к заметному ухудшению характеристик качества обслуживания по сравнению с любыми другими типами входного потока.

92 Анализ телекоммуникационных систем.

Проведенные исследования показывают [2,8], что для некоторых цифровых сетей связи, например Ethernet, Telnet, Opnet и др., адекватными являются модели, в которых интервалы времени входного потока пакетов описываются на основе экспоненциального распределения, а время обслуживания на основе ПРВ с долговременной зависимостью, например, Парето или Вейбулла.

Допустим, что имеется цифровая система, состоящая из буфера неограниченного объема и одного сервера, с временем обработки, подчиняющимся ПРВ Парето. Входной поток будем считать простейшим со средней интенсивностью  . Требуется определить среднее время нахождения пакета в системе и среднюю длину очереди в буфере.

На основе ПРВ Парето можно определить среднее время обработки одного пакета на сервере:

,

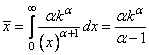где   - параметры ПРВ Парето. Входную нагрузку определим как

.

Зная среднее время обработки   одного пакета на сервере и величину входной нагрузки  , можно определить среднее время ожидания пакета в буфере с помощью формулы Полячека-Хинчина:

,

где   - второй момент для времени обслуживания, который определяется как

.

Для дальнейших расчетов данную величину удобно выразить через дисперсию и математическое ожидание времени обслуживания:

,

откуда

.

В случае распределения Парето величина

и

.

Таким образом, среднее время ожидания пакета в буфере такой цифровой системы определяется выражением

.

Используя формулу Литтла, найдем среднее число пакетов в буфере:

.

Аналогично можно определить среднее время пребывания пакета в системе, а также среднее число пакетов. Кроме того, подставляя вместо величин   и   значения для других ПРВ, например, Вейбулла, можно подобным образом выполнять анализ цифровых систем для других ПРВ.