85.Модель Энгсета. Схема m-серверной системы с полными потерями

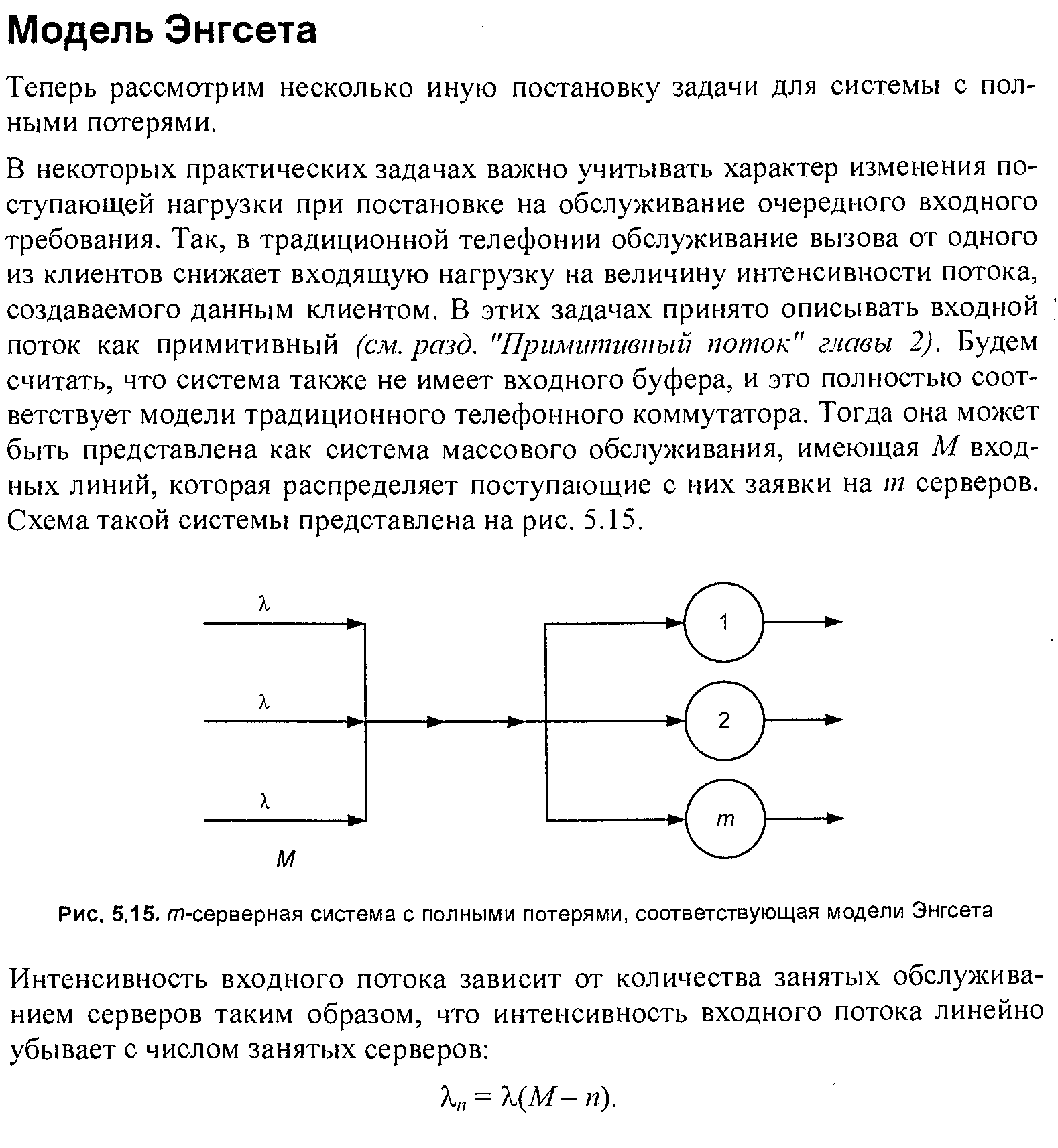
86. Диаграмма интенсивностей переходов для m-серверной системы с полными потерями, соответствующей модели Энгсета

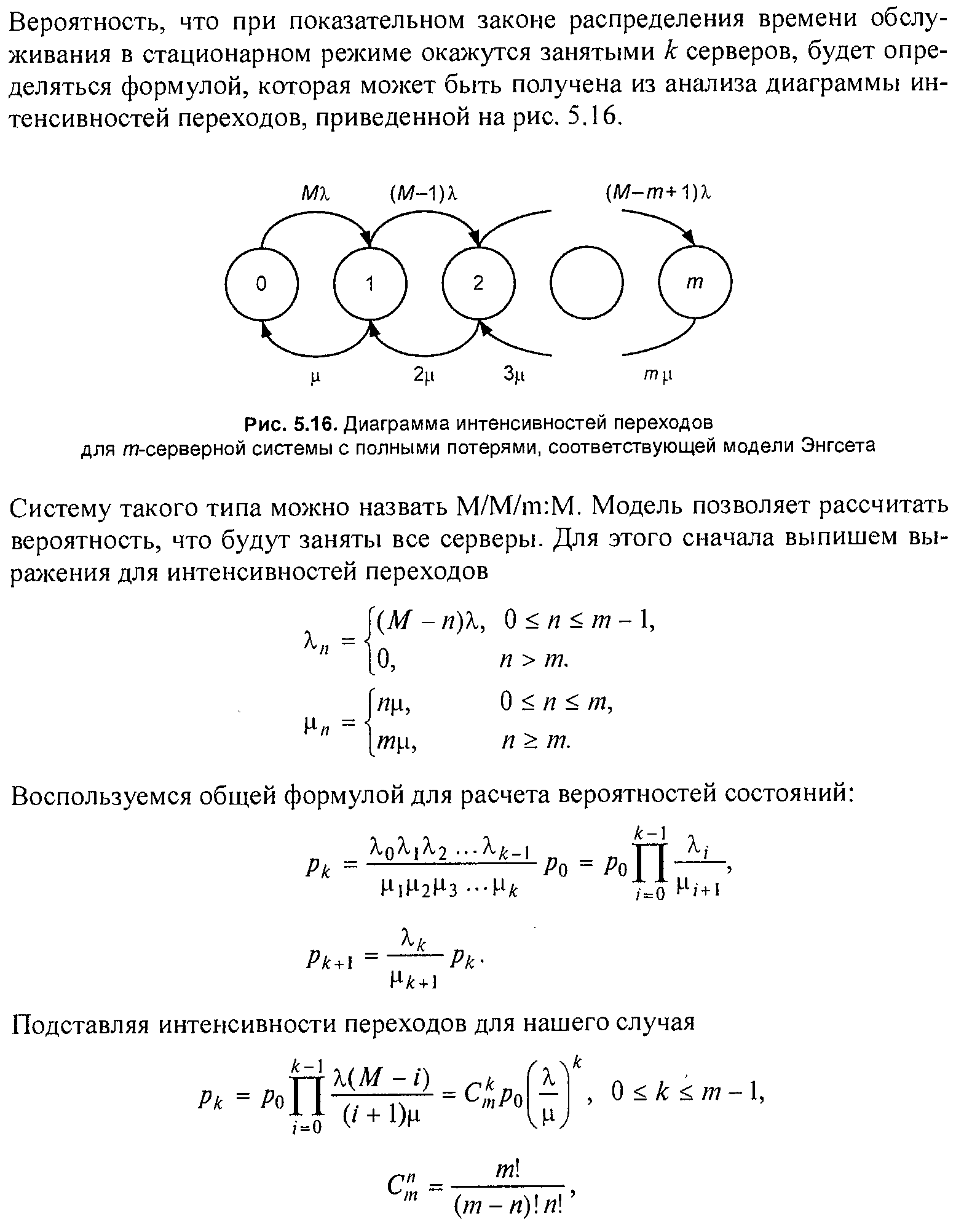
№ 87.Анализ систем с произвольным распределением времени обслуживания.

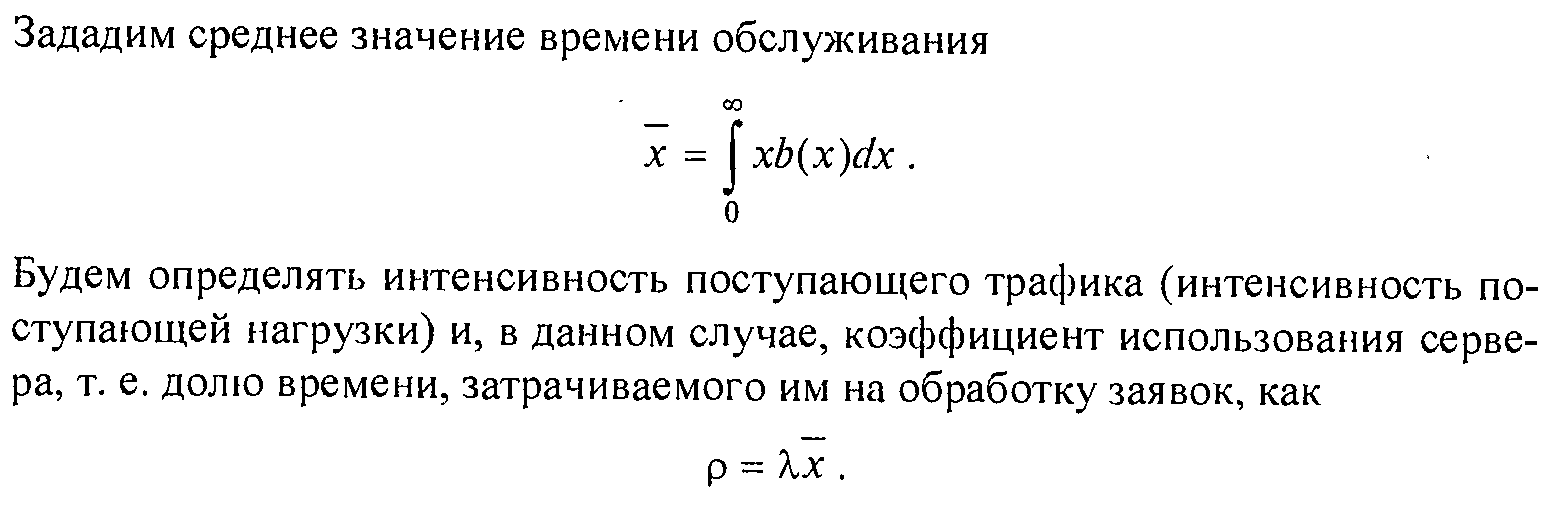
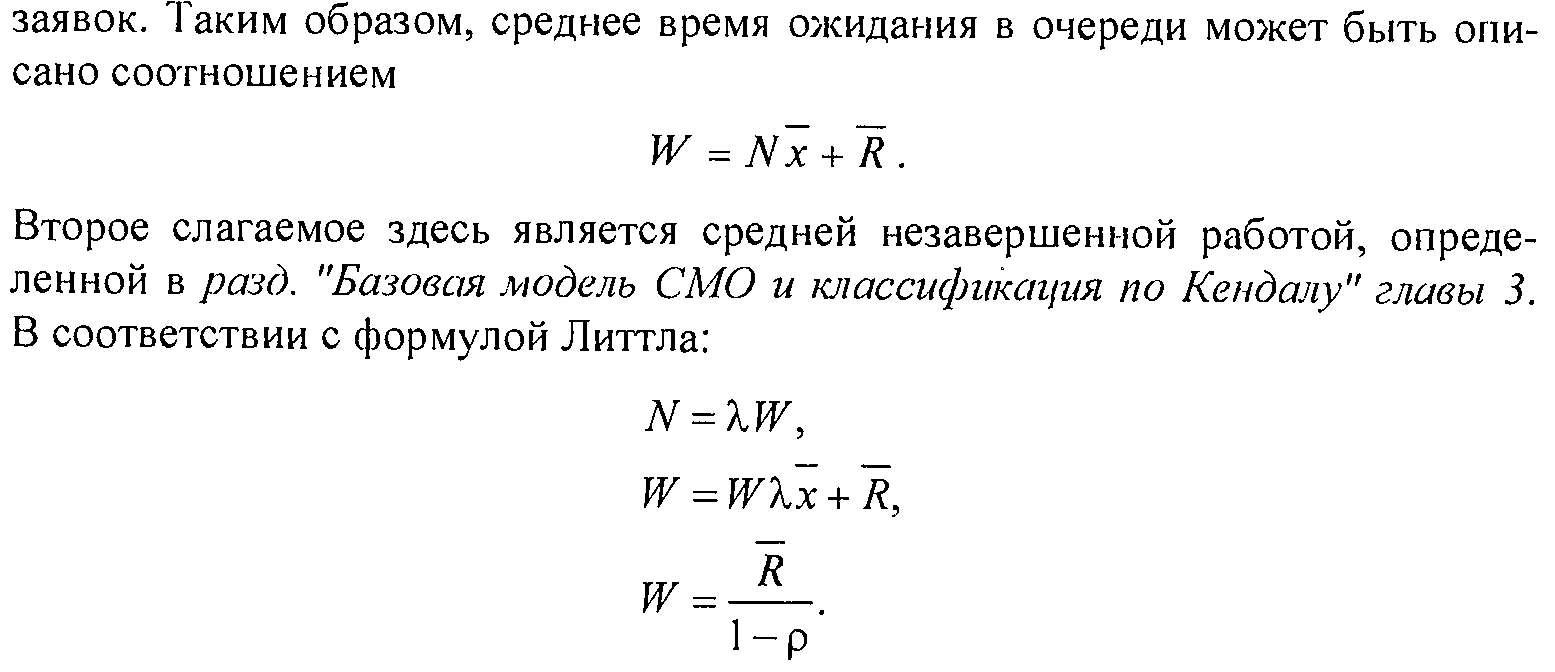
88. . Самоподобные (фрактальные) модели трафика.

Во всех рассмотренных ранее моделях потоков событий считалось, что веро­ятность появления следующего события зависит только от времени, прошед­шего с момента совершения предыдущего события, и не зависит от всей пре­дыстории появления событий ранее. Однако в некоторых случаях такие мо­дели не могут адекватно отразить реальный поток событий. Поэтому кроме потоков без последействия приходится рассматривать и такие, в которых ве­роятность появления следующего события зависит от наступления событий в предыдущих интервалах времени. Типичным примером таких потоков явт ляются потоки с ограниченным последействием. Для них задается конечный набор функций распределения для соседних интервалов т* между поступле­нием к событий. Одним из наиболее типичных потоков с ограниченным по­следействием является стационарный поток с запаздыванием — поток Паль-, ма. Функции распределения вероятности для интервалов между соседними событиями потока Пальма задаются через условную вероятность ф₀(t) отсут­ствия событий в интервале длиной /, если в начале этого интервала поступало событие, следующим образом:

Здесь величина X выражает интенсивность потока и равна, как обычно, об­ратной величине среднего промежутка времени между соседними события­ми. При экспоненциальной функции ф₀(0 = е~^ь поток Пальма превращается в пуассоновский. Иногда его называют потоком Эрланга первого порядка. Производя "просеивание" потока Пальма, т. е. отбрасывая каждое второе, каждое третье, каждое п-е событие, получают потоки, которые называют потоками Эрланга второго порядка, третьего порядка и, соответственно, п-го порядка. Для потока Эрланга порядка п функция распределения имеет вид:

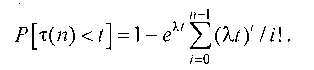
Введение моделей с последействием позволяет отразить свойства потоков с памятью, однако приведенные выше модели Пальма и Эрланга оказываются малоподходящими, если в потоке событий обнаруживается так называемая долгосрочная зависимость (long range dependent) или самоподобие (self­similarity). На интуитивном уровне это означает, что число событий на задан­ном временном интервале может зависеть от числа событий, поступивших в весьма отдаленные от него интервалы времени. При этом часто процесс но­сит пачечный (bursty) характер. Типичным способом измерения такой зави­симости для случайных процессов является определение функции корреляции. Будем рассматривать в качестве значения случайного процесса число собы­тий, поступающих в систему в единицу времени. Это, конечно, неотрица­тельная случайная величина. Случайный процесс будем рассматривать как дискретную последовательность таких случайных величин, т. е. аргументом будем считать порядковый номер такой единицы времени:

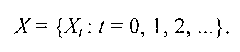
Положим, что все рассматриваемые далее случайные процессы относятся к стационарным случайным процессам с ограниченной ковариацией, т. е.

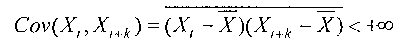
с дисперсией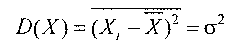

и автокорреляционной функцией

Для того чтобы охарактеризовать принадлежность процесса к классу процес­сов, имеющих долгосрочную зависимость или самоподобие, необходимо рас­смотреть агрегированные из него процессы, построенные с помощью усред­нения значений исходного процесса на непересекающихся временных интер­валах:

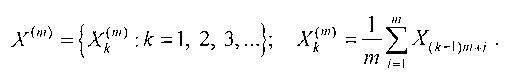
Очевидно, что агрегированные процессы также будут стационарны и имеют ограниченную ковариацию.

Как метео определил в своей работе [11] один из патриархов отечественной теории телетрафика В. И. Нейман, "три источника и три составные части тео­рии самоподобных процессов" выражены в медленном убывании дисперсии, долгосрочной зависимости и флуктуационном характере спектра мощности таких процессов.

Убывание дисперсии асимптотически описывается соотношением

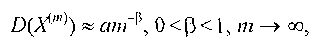(2.1)

т. е. вариация агрегированных процессов — средних выборок — уменьшается медленнее, чем величина, обратная размеру выборки.

Долгосрочной зависимостью в самоподобных процессах называют наличие расходимости автокорреляционной функции процесса:

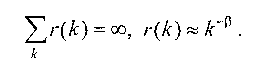(2.2)

Это означает, что спад автокорреляционной функции происходит гиперболи­чески медленно.

Наконец, говоря о флуктуационном характере спектра мощности, понимают под этим аналогию со спектром мощности флуктуаций электронного потока:

(2.3)

где

Наличие перечисленных выше свойств у случайного процесса означает, что его автокорреляционная функция совпадает с автокорреляционными функ­циями агрегированных процессов точно

или асимптотически

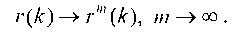
Собственно эти соотношения и определяют название самоподобного процес­са: корреляционные свойства такого процесса, усредненного на различных временных интервалах, остаются неизменными.

Важнейшим параметром, характеризующим "степень" самоподобности слу­чайного процесса, является параметр Хёрста (Hurst).

Для выборочного случайного набора Xj (J = 1, N) можно определить выбо­рочное среднее

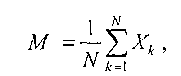
выборочную дисперсию

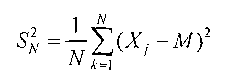
и интегральное отклонение

Определим изменчивость случайного процесса на интервале N как неубы­вающую функцию длины интервала

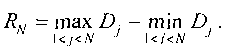
Херстом было показано, что для большинства естественных процессов отно­шение

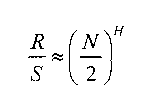
или иначе

при больших N.

Величина Н получила название параметра Херста и лежит в интервале 0,5 <H<1,0. Для процессов, не обладающих свойством самоподобия, величи­на параметра Херста равна 0,5. Для самоподобных процессов с долгосрочной зависимостью этот параметр изменяется в пределах 0,7—0,9. Параметр р, ко- , торый был введен выше для задания асимптотических свойств характеристик ! самоподобныхслучайных процессов, может быть выражен через параметр '^Херста:

Можно оценить другим способом степень самоподобия процесса, определив непосредственно величину β из соотношения (2.1):

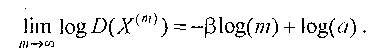
Таким образом, построив в логарифмическом масштабе зависимость отноше­ния R/S от логарифма числа выборок или зависимость логарифма дисперсии для агрегированных процессов от логарифма степени агрегирования, можно

Рис. 2.10. Аппроксимирующая кривая

Впервые на самоподобие процессов, описывающих трафик в пакетных сетях, обратили внимание в начале 90-х годов прошлого века. Лиланд (W. Е. Leland) и его коллеги (М. S. Taqqu, W. Willinger, D. V. Wilson) выступили с докладом и опубликовали статью [2], которая многократно цитировалась целое десяти­летие. В ней были приведены результаты экспериментального анализа тра­фика в пакетной сети и показано, что распределение числа пакетов в единицу времени очень хорошо описывается самоподобным случайным процессом с параметром Херста около 0,65—0,8. В начале этой статьи приводятся очень наглядные графики зависимости числа пакетов в единицу времени. Мы при­ведем некоторые из этих графиков (рис. 2.I I). По горизонтальной оси в них отложено текущее время, так что в дискретном представлении его макси­мальное значение равно одной тысяче единиц, а единица измерения времени на каждом графике различна: от 0,01 секунды до 100 секунд. Обычно эту ве­личину называют временной шкалой. По вертикальной оси отложено число пакетов в сети, поступившее за выбранную единицу времени.

Уже первый взгляд на графики и их сравнение наводят на мысль о чрезвы­чайном сходстве. Это и есть проявление самоподобия. Процессы, описываю­щие трафик в различных временных масштабах, шкалах, имеют близкие ста­тистические свойства.

Простейшими самоподобными процессами являются фрактальное броунов­ское движение и фрактальный гауссовский шум.

О 1000

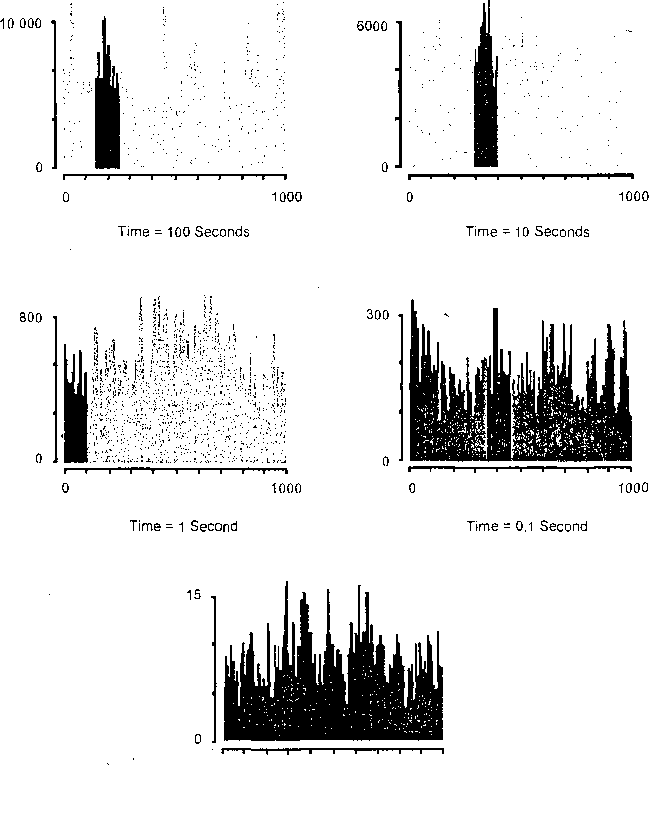
Time = 0,01 Second

Рис. 2.11. Экспериментальные данные о трафике в сети

Одним из основных свойств фракталов является самоподобие. В самом про­стом случае небольшая часть фрактала содержит информацию обо всем фрактале. Определение фрактала, данное Мандельбротом, звучит так: "Фрак­талом называется структура, состоящая из частей, которые в каком-то смысле подобны целому".

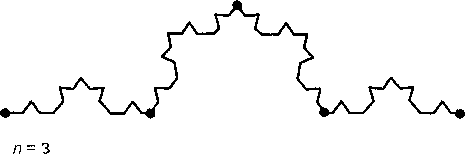
Простейший фрактал имеет вид, представленный на рис. 2.12.

За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменя­ется на ломаную, в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал. Наглядно увидеть рост фракталов можно, используя апплет на сайте: http:// «ww.shodor.org/master/fractaI/software/Snowflake.htmI.

Нормированное фрактальное броуновское движение (Fractal Brownian Mo­tion, fBM) с параметром Херста Н— это случайный процесс (X,), > ₀, обла­дающий следующими свойствами:

• X, имеет стационарные нормально распределенные случайные прира­щения;

• для любыхt1,t1;

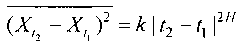• для любых t1 t2;

ОХ, — нормально распределенная случайная величина для любого / > 0.

Из последнего пункта также можно сделать следующий вывод:

Последовательность приращений fBM, т. е. его производная в определенном смысле, образует фрактальный гауссовский шум (Fractal Gaussian Noise,JGN).

Фрактальный гауссовский шум (черный шум) — этО| стационарный гауссов­ский процесс с заданными параметрами (т, сг) и автокорреляционной функ­цией

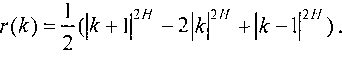
Исходя из самых общих соображений, можно показать, что параметр Херста сохраняется при суммировании любого конечного числа независимых само­подобных процессов с фиксированным параметром самоподобия.

Действительно, для суммы независимых случайных процессов функция кор­реляции равна сумме функций корреляции слагаемых, если каждая из функ­ций имела асимптотическое поведение в соответствии с выражением (2.1). Тем самым сохраняются все важнейшие характеристики самоподобия.

Одной из таких характеристик является величина выбросов процесса. Для самоподобных процессов характер выбросов сохраняется при рассмотрении процесса в различных масштабах времени. Это означает, что если вы будете записывать нагрузку на каком-либо элементе сети с дискретностью, напри­мер, 10 миллисекунд, то, рассматривая график изменения нагрузки во време­ни на интервалах 10 секунд, 10 минут или 10 часов, вы не заметите сущест­венных различий в поведении кривой. В этом смысле самоподобие графиков может быть охарактеризовано соотношением