51. Имитационные модели смо, основные задачи построения программы имитации

52. Условия, накладываемые на быстродействие алгоритмов имитации

В настоящее время имитационные модели строятся в виде программ, разра­батываемых на обычных языках программирования, таких как С, С++, Java, или на специализированных языках и в специализированной визуальной среде.

Построение программы имитации поведения СМО основано на программи­ровании цепочки событий, начиная от входных требований, поступающих в случайные моменты времени, занятия и освобождения серверов в соответст­вии со случайным характером длительности обработки каждого требования, помещения и чтения событий из очереди в соответствии с дисциплиной об­служивания и доступностью серверов. Итогом работы программы является получение статистических отчетов о процессах в системе. Поскольку интерес представляют некоторые усредненные характеристики типа среднего по всем требованиям времени нахождения в системе, то для получения устойчивых статистических оценок требуется проимитировать весьма большое количест­во рабочих циклов моделируемой системы. Пусть, например, анализируется система с блокировкой входящих требований. Если уровень блокировок в системе характеризуется величинами порядка Ю^-5, то для получения стати­стически устойчивых оценок (с точностью порядка 1%) придется имитиро­вать прохождение через систему не менее нескольких миллионов требований. Это накладывает условия на быстродействие алгоритмов имитации. Медлен­ные алгоритмы будут существенно снижать ценность имитационной модели и требовать повышенных вычислительных ресурсов.

Рассмотрим простейший алгоритм имитации системы с одним сервером, без приоритетов, с неограниченным размером входного накопителя. В алгоритме используются перечисленные ниже сущности и их атрибуты-переменные.

• Сущность SERVER имеет атрибут busy, который может принимать два значения busy=0, если SERVER находится в состоянии idle (свободен), и busy= 1, если SERVER находится в состоянии busy (занят). Другой атрибут сущности SERVER назовем ctime. Это момент времени, в который обслу­живание поступившего на сервер требования будет завершено. Если сер­вер свободен, то данный атрибут может считаться бесконечно большим и ему присваивается наибольшее машинное число.

• Сущность QUEUE имеет атрибутом число требований, находящихся в очереди, не считая того, которое находится на сервере на обслуживании. Обозначим соответствующую переменную qsize.

• Сущность AGEN — это механизм, определяющий моменты поступления в систему требований. Атрибут atime будет представлять текущий момент поступления очередного входного требования. Будем считать, что atime генерируется некоторым датчиком входного потока событий с помощью генератора случайных интервалов, описанного выше (см. paid. "Модели потоков событий" главы 2'), и считывается программой имитации.

□. Сущность SGEN — это механизм, определяющий случайное время обслу­живания требования, поступившего на сервер. Атрибут stime будет пред­ставлять случайную величину, задающую время обслуживания того тре­бования, которое находится в данный момент на сервере.

52. Условия, накладываемые на быстродействие алгоритмов имитации

55. Сети Петри – эффективная модель СМО.

56. Определение сети Петри. Графическая интерпретация сети Петри.

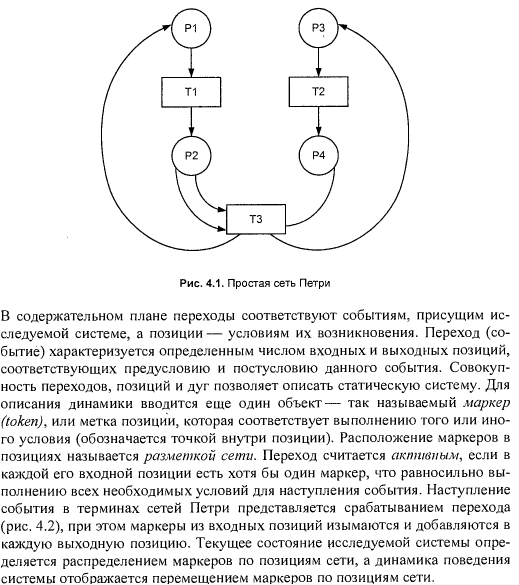
57. Приоритетные, структурированные и раскрашенные сети Петри, их назначение

58. Пример цветной сети Петри, моделирующая поведение отдельного абонента телефонной сети.

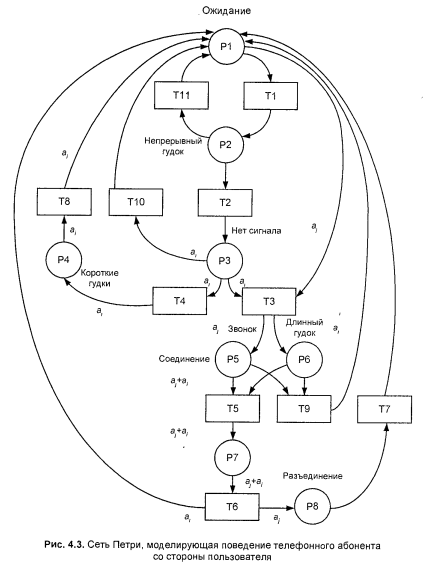
59. Стохастические сети Петри, пример работы такой сети

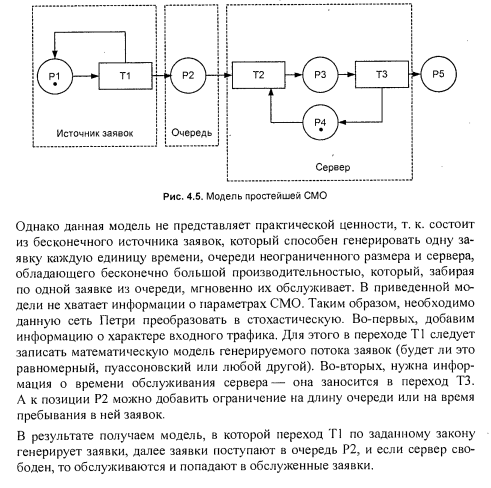
60. Средства программной реализации сетей Петри. Система Visual Petri.

61. Аналитические методы в теории телетрафика.

62. Вероятностная модель СМО.

63. Дискретные и непрерывные цепи Маркова.

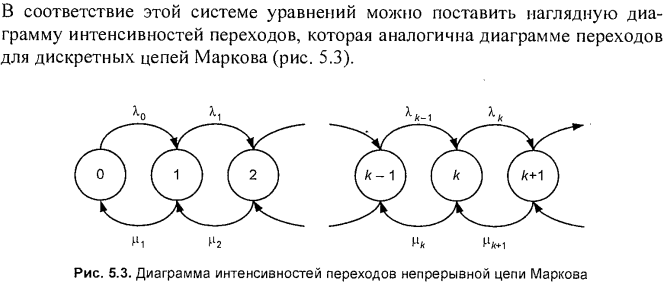
64. Определение однородной цепи Маркова, неприводимой цепи.

65. Различные виды состояний цепи: возвратное, невозвратное, поглощающее, периодическое, апериодическое.

но.

66. Пример изображения цепи Маркова с конечным числом состояний.

67. Уравнение Чепмена-Колмогорова для однородных цепей Маркова.

Можно показать, что эти вероятности связаны между собой, так называемым уравнениями Чепмена-Колмогорова.(Chapman - Kolmogorov)

.

Для однородных цепей Маркова эти уравнения упрощаются так как

.

И сводятся к анализируемым выше.