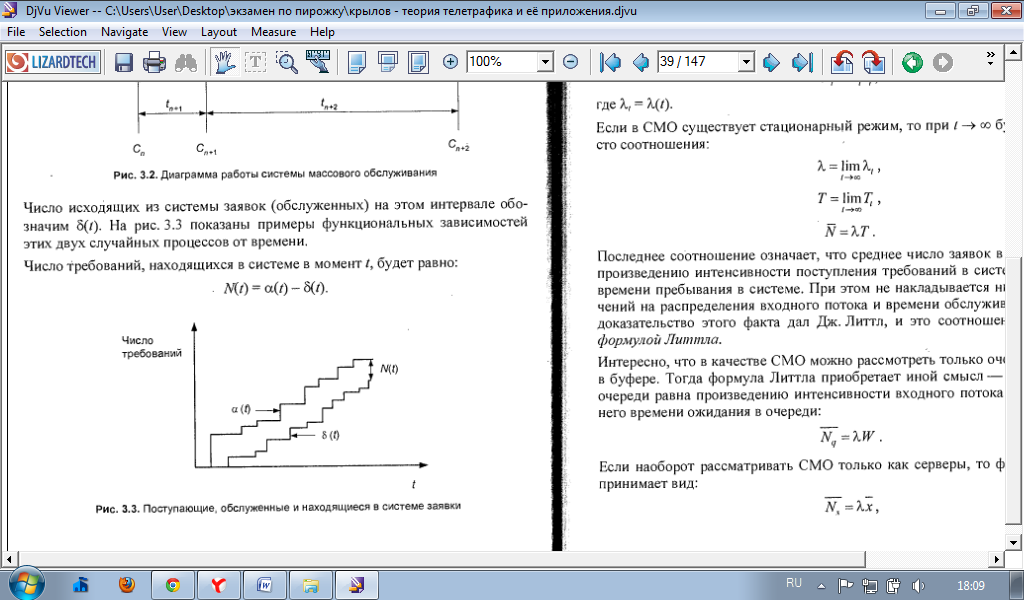
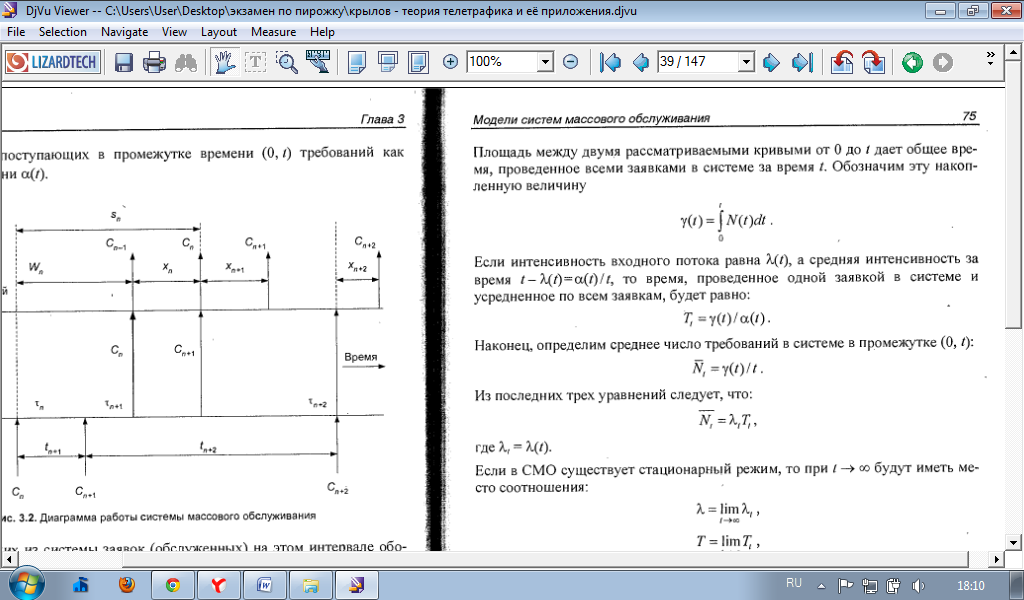
41. Формула Литла для определения среднего числа заявок в системе.

42. Определение коэффициента использования для описания работы СМО.

Одним из основных параметров, которые используются при описании СМО, является коэффициент использования. Это фундаментальный параметр, так как он определяется как отношение интенсивности входного потока к пропускной способности системы. Поскольку пропускная способность СМО содержащей m серверов может быть определена как: , то коэффициент использования может быть определен как:

.

Нетрудно видеть, что коэффициент использования равен в точности интенсивности нагрузки, если СМО с одним сервером и в m раз меньше для систем с m серверами. Величина коэффициента использования равна среднему значению от доли занятых серверов и .

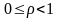Если в СМО типа G/G/1 существует стационарный режим и можно определить вероятность того, что в некоторый случайный момент сервер будет свободный, то

.

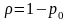43-44. Понятие остаточного времени обслуживания для функционирования СМО. Понятие незавершенной работы при функционировании СМО.

По определению незавершенная работа в каждый момент времени - это остаточное время, необходимое для освобождения системы от всех требований, находящихся в ней к этому моменту. Очевидно, что для системы G/G/1 значение незавершенной работы непосредственно перед поступлением n-го требования в точности равно времени w_n . Таким образом, последовательность этих значений будет образовывать дискретную марковскую цепь, вероятности переходов которой могут быть определены по характеристикам входного потока и времени обслуживания.

Иногда незавершённую работу называют виртуальным временем ожидания в момент времени t, так как при обслуживании в порядке поступления незавершённая работа показывает, как долго должно было ожидать начала обслуживания в очереди требование, поступившее в момент времени t.

Рассмотрим два случая поступления требования С_n в систему - поступление в занятую систему (Рис. 6.1) и в свободную систему (Рис. 6.2).

Рис. 6.1 Случай, когда требование C_n+1 поступает в занятую систему.

Рис. 6.2 Случай, когда требование C_n+1 поступает в свободную систему.

Нетрудно видеть, что для первого случая

.

Для второго случая .

Определим случайную величину, равную разности между временем обслуживания требования с номером n и промежутком времени между поступлениями n+1 и n-го требований .

Фундаментальное свойство этой случайной величины состоит в том, что для стабильных СМО, т.е. имеющих стационарное распределение вероятностей состояний, ее математическое ожидание должно быть отрицательным. Смысл этого утверждения понятен из определения. Очевидно, что в среднем время обслуживания должно быть меньше времени между поступлениями соседних требований

45. Смо с полнодоступными и неполнодоступными серверами.

Системы с несколькими серверами могут по-разному распределять их ресурс для обслуживания поступающих заявок. Если любой свободный сервер может обслуживать любую поступающую заявку, то говорят о полнодоступном включении серверов. Если за определенными серверами закрепляются заявки, поступающие только с определенных входных линий, то говорят о неполнодоступном включении серверов (НВ).

В уравнениях Чепмена-Колмогорова неполнодоступность можно отразить введением специальной функции, зависящей от состояния системы, значение которой определяет вероятность получения доступа к серверу. Иначе говоря, речь идет о том, что вероятность блокировки в неполнодоступных схемах включения серверов зависит не только от количества серверов, но и от способа их включения для обслуживания, т.е. определяется вероятностями занятия определенных, а не любых серверов.

Обозначим:

- функцию состояния k, значение которой равно вероятности обслуживания заявки, поступившей в СМО в этом состоянии. Стационарное распределение вероятностей в этом случае будет зависеть как от параметра входного потока, так и от значения .

Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением изображена на рисунке 1.21:

Рис. 1.21 Диаграмма интенсивностей переходов для СМО с m серверами, явными потерями и неполнодоступным включением.

Запишем уравнения баланса

.

Для нашего случая входной поток пуассоновский и можно положить

Тогда решение для стационарного распределения вероятностей состояний дается формулой

Полученное выражение называют третьим распределением Эрланга.