1. Определение средней интенсивности трафика. Единица измерения интенсивности трафика.

Интенсивность трафика. При этом чаще говорят о средней интенсивности трафика (нагрузки) на некотором заданном пуле (наборе) ресурсов. Если в каждый момент времени t из заданного интервала (t₁,t₂) число занятых обслуживанием трафика ресурсов из данного набора равно А(t), то средняя интенсивность трафика будет

Величина интенсивности трафика характеризуется как среднее число ресурсов, занятых обслуживанием трафика на заданном интервале времени. Единицей измерения интенсивности нагрузки является один Эрланг (1 Эрл, 1 Е)., т.е. 1 эрланг– это такая интенсивность трафика, которая требует полной занятости одного ресурса, или, иначе говоря, при которой ресурсом выполняется работа величиной в одно секундо-занятие за время в одну секунду. В американской литературе иногда можно встретить другую единицу измерения, называемую CCS– Centrum (or hundred) Calls Second (гектосекундозанятия). Число CCS отражает время занятия серверов в 100 секундных интервалов за 1 час. Интенсивность, измеренную в CCS, можно пересчитать в Эрланги по формуле 36CCS=1 Эрл.

Трафик, создаваемый одним источником и выраженный в часо-занятиях, равен произведению числа попыток вызовов с за определенный интервал времени Т на среднюю длительность одной попытки t: у = с t (ч-з). Трафик можно вычислить тремя разными способами:1) пусть число вызовов с в течение часа равно 1800, а средняя длительность занятия t = 3 мин, тогда Y = 1800 выз. /ч. 0,05 ч = 90 Эрл;

2) пусть в течение времени Т фиксируются длительности t_i всех n занятий выходов некоторого пучка, тогда трафик определяют так:

3) пусть в течение времени Т выполняется наблюдение через равные промежутки времени за количеством одновременно занятых выходов н екоторого пучка, по результатам наблюдений строят ступенчатую функцию времени x(t).

Трафик в течение времени Т может быть оценен как среднее значение х(t) за это время:

2. Измерения трафика. Диаграмма Ганта. Нахождение объема пропущенного трафика. Средняя интенсивность трафика.

Сначала рассмотрим, как можно отображать работу СМО, имеющую несколько ресурсов, которые одновременно обслуживают некоторый трафик. Одним из наиболее наглядных и часто употребляемых способов изображения процесса обслуживания заявок пулом серверов является диаграмма Ганта (Gantt). Эта диаграмма представляет собой прямоугольную систему координат, ось абсцисс которой изображает время, а на оси ординат помечаются дискретные точки, соответствующие серверам пула.

Далее, каждый интервал времени, когда сервер занят обслуживанием заявки из входного потока, отмечается отрезком жирной горизонтальной прямой.

На рис. изображена диаграмма Ганта для системы с тремя серверами. В первые три интервала времени (будем считать их для определенности секундой) заняты первый и третий серверы, следующие две секунды — только третий, затем одну секунду работает только второй, потом, две секунды второй и первый, и последние две секунды работает только первый.

П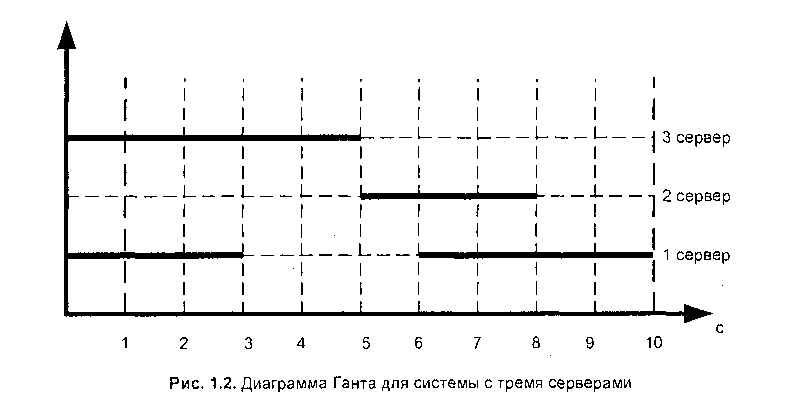 остроенная диаграмма позволяет произвести расчеты объема трафика и его интенсивности. Сразу заметим, что построенная диаграмма Ганта отражает только обслуженный или пропущенный трафик (traffic carried), поскольку ничего не говорит о том, поступали ли в систему заявки, которые не смогли быть обслужены серверами. При построении диаграммы Ганта для поступающего трафика (traffic offered) нужно строить горизонтальные отрезки, ассоциируя их начала с моментами поступления заявки, длины — с требуемым временем обслуживания и располагая их по оси ординат таким образом, чтобы такие отрезки не пересекались.

В любом случае, объем трафика вычисляется как суммарная длина всех отрезков диаграммы Ганта. Разность между объемами поступающего и пропущенного трафиков называется объемом избыточного трафика (overflow traffic). Приведенная выше диаграмма позволяет найти объем пропущенного трафика за время в 10 секунд

Свяжем с каждым временным интервалом, отложенным по оси абсцисс, це­лое число, равное количеству серверов, занятых на этом единичном интерва­ле. Эта величина была нами ранее обозначена как A(t)— мгновенная интен­сивность. Для нашего примера, где дискретность измерения составляет 1 секунду, можно представить мгновенную интенсивность следующей после­довательностью:

А0)={2, 2, 2, 1, 1, 1,2, 2, 1, 1}.

Найдем теперь среднюю за период в 10 секунд интенсивность трафика. В соответствии с приведенной выше формулой получим

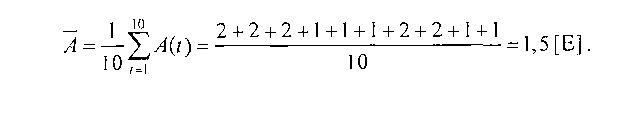
Разность между объемами поступающего и пропущенного трафиков называется объ­емом избыточного трафика (overflow traffic).

Средняя интенсивность потока требований – соотношение количества не обработанных заявок в длине интервала времени. Эту величину принято обозначать Отрезки, представляющие собой интервалы занятости (обслуживания) имеют различную, случайную длину. Поскольку число таких отрезков равно в точности п, то можно суммарную длину этих отрезков (обозначим ее s) записать в виде произведения где х — средняя длительность занятия (обслуживания).

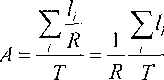
Единицей измерения интенсивности трафика здесь также является эрланг.