33.Пропорциональная система «Модулор» и ее применение в творчестве Ле Корбюзье

Проблему согласования метрических мер с пропорциональной системой, в основе которой лежали бы размеры человека, изучал
 Ле Корбюзье. Свою линейку пропорций он назвал модулером. По его
 словам «Модулор» — это средство измерения, основой которого являются рост человека И математика»

О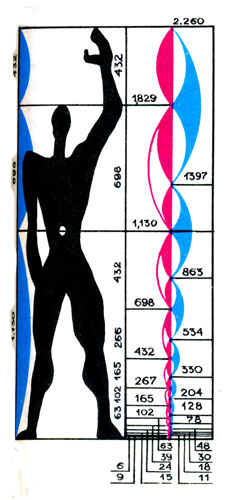 снову шкалы модулора составляют пропорции человеческого тела и математические вычисления. Они являются исходными размерами для строительства, позволяя размещать архитектурные элементы соразмерно человеческой фигуре. С одной стороны, по человеку с поднятой рукой определяются точки занятого пространства: нога - солнечное сплетение, солнечное сплетение - голова, голова - кончик пальцев поднятой руки - три интервала (триада), обуславливающие серию золотого сечения, называемую рядом Фибоначчи. С другой стороны, создается простой квадрат, его удвоение и два золотых сечения. Объекты строительства представляют собой весьма различные вместилища человека или продолжение его жестов (например, машина, мебель, книга). Модулор помогает выбрать наиболее оптимальные размеры объекта и его составляющих, соответствующие росту и пропорциям человека

В основу своей пропорциональной системы Ле Корбюзъе положил

средний рост мужчины—шесть футов (1,83 м). Приняв его за исходную величину, он построил «золотой ряд»: 1,829; 1,13: 0,699: 0,432; 0,267; 0,165; 0.102... м, который назвал «красной шпалой», В основу
 второй, «синей шкалы» была положена высота человека с поднятой
 рукой — 2.26 м. Соответственно, второй «золотой ряд» выражается
 в следующих числах: 2,26; 1,397; 0,863; 0,534; 0,83; 0,204: 0,126... ж. Причем каждый член «синей шкалы» может быть подучен удвоением
 предыдущего члена «красной шкалы» Достоинством этих взаимосвязанных золотых рядов является то. что
 их числовые величины согласуются со всеми основными параметрами


человека и следовательно их применение в проектировании упрощает
взаимосвязь строительных габаритов с размерами человека

На базе модулера Ле Корбюзье спроектировал жилой дом в Марселе,


завод около Сен-Дью и другие сооружения

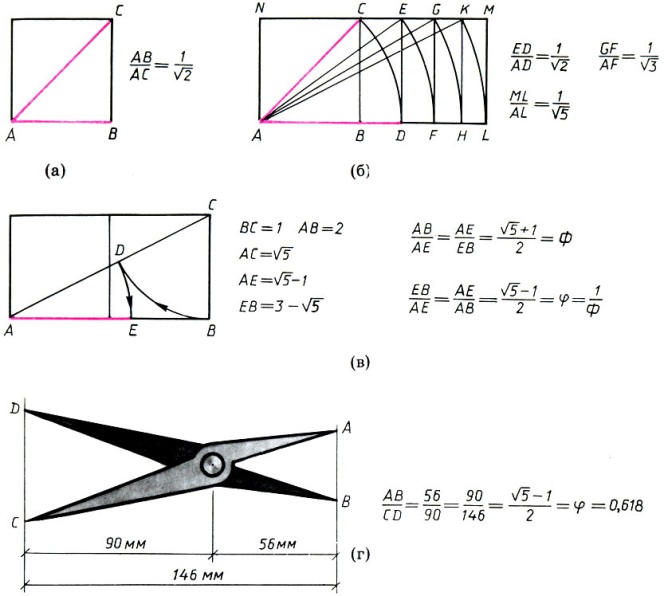
34.Иррациональные пропорции в архитектуре Квадрат и его производные служили основой для многих пропорциональных систем. На базе двух квадратов можно с помощью несложных геометрических построений получить большинство иррациональных отношений, которые употреблялись в архитектуре:

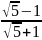—-~0,382… 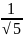=0,447…; 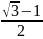=0,618; =0,704..; =0,809;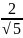 =0,894

Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе 'двойной квадрат' (в). Помпейскйй пропорциональный циркуль, установленный на золотое сечение (г)

35.Рациональные пропорции в архитектуре

Учение, о числах как основе соразмерности зародилось еще в Месопотамии и Египте, обладавших высокой строительной культурой. Дальнейшее развитие науки о числи как основе рационального познания


мира связано с Пифагорейской школой (VI в. до я. о,— VI в. к. э.),


согласно которой вселенная представляет собой гармоническую систему


чисел и ил отношений. Многие пифагорейны имели непосредственное


отношение к практическим требованиям архитектуры и художественного ремесла и стремились найти удобные приемы для гармонизации


произведений искусства и архитектуры.

Пропорциональные системы позволяли зодчим без масштабного


чертежа определять размеры возводимых частей здания, исходя из


принципа, положенного в основу разбивки плана. Таким образом, про-


порционнровапие для зодчих древности служило прежде всего рабочим


методом, дающим возможность заранее, на основе арифметической закономерности или геометрического построения, определять будущие


размеры здания.