Согласно выражению (3) передаточная
функция ЛНСС имеет вид рациональной
функции, т.е. отношения двух полиномов
от s. В соответствии
с теоремой о разложении многочлена
каждый многочлен степени n
может быть единственным образом
представлен (факторизован) в виде
произведения постоянной и n
линейных множителей
где sk
– корни многочлена, корню sk
кратности mk
соответствует mk
множителей (s-sk).
При этом для многочленов с действительными
коэффициентами комплексные корни
обязательно встречаются как комплексно
- сопряженные пары. Иначе соответствующие
коэффициенты многочлена не будут
действительными. Очевидно, что каждая
такая пара множителей
Здесь
Полюса и нули передаточной функции
![]() ,
,![]() перемножением может быть объединена
в действительный квадратичный множитель
перемножением может быть объединена
в действительный квадратичный множитель
![]() .
Таким образом, рациональная передаточная
функция системы с действительными
коэффициентами может быть представлена
в виде
.
Таким образом, рациональная передаточная
функция системы с действительными
коэффициентами может быть представлена
в виде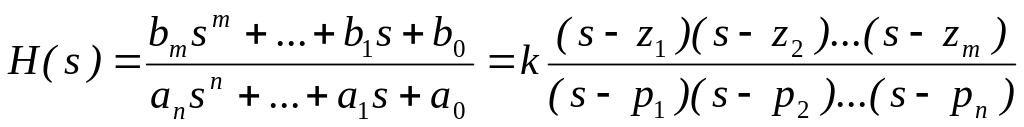 . (6)
. (6)![]() - корни многочлена – числителя, они
называются нулями H(s),
- корни многочлена – числителя, они
называются нулями H(s),![]() - корни многочлена – знаменателя
называются полюсами H(s),
- корни многочлена – знаменателя
называются полюсами H(s),
![]() -
усиление системы (gain).
В точке полюса
-
усиление системы (gain).
В точке полюса
![]() .
При этом каждая
пара множителей с комплексно-сопряженными
корнями можем быть объединена в один
квадратичный член.
.
При этом каждая
пара множителей с комплексно-сопряженными
корнями можем быть объединена в один
квадратичный член.
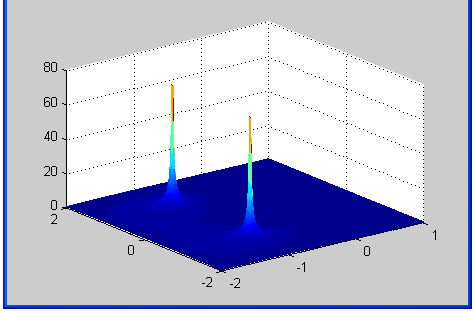
Пример. Система второго порядка с
передаточной функцией
График передаточной функции.
Код:
[x,y]=meshgrid(-2:0.01:1, -2:0.01:2); s=x+y*j;
H=(s+0)./((s+1).^2+1);
mesh(x,y,abs(H))
![]() .
Нули и полюса:
.
Нули и полюса:
![]()

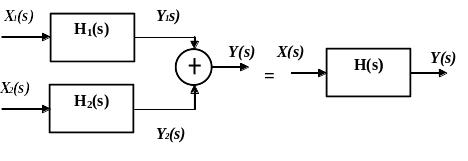
Последовательное соединение систем:
Передаточная функция
Параллельное соединение систем:
Передаточная функция
Таким образом, ПФ последовательного
соединения систем равна произведению,
параллельного соединения – сумме
передаточных функций отдельных систем.
Передаточные функции соединений систем

![]()
![]()

Y1(s)
Y(s)
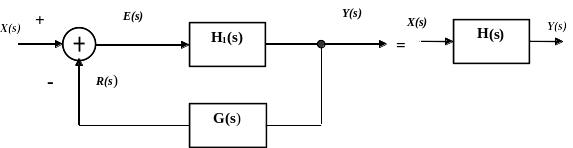
Передаточная функция системы с замкнутой
отрицательной обратной связью (ООС)
Отсюда
т.е. передаточная функция системы с ООС
равна отношению передаточной функции
канала прямой передачи H1(s)
к (1 - петлевое усиление цепи обратной
связи). В данной схеме петлевое
усиление цепи обратной связи есть
При
Аналогичный вид имеют выражения для
частотных характеристик систем,
поскольку
![]()
![]()
![]() ,
,![]() .
.![]()
![]() - зависит только от обратной связи.
- зависит только от обратной связи.![]() .
.

Поэтому передаточную функцию реальной
системы можно представить в виде
каскадного (последовательного) соединения
систем первого и/или второго порядка
с вещественными коэффициентами, т.е. в
виде
где Hi(s)
– передаточная функция системы второго
или первого порядка
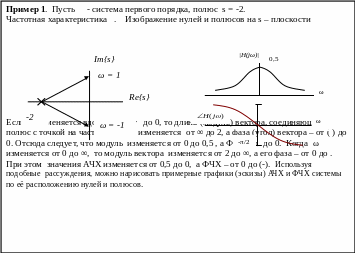
Для системы первого порядка
Если
Следовательно, АЧХ
Фазо - частотная характеристика
равна сумме углов нулей системы минус
сумма углов полюсов. Углы отсчитываются
от действительной оси плоскости s.
![]() ,
,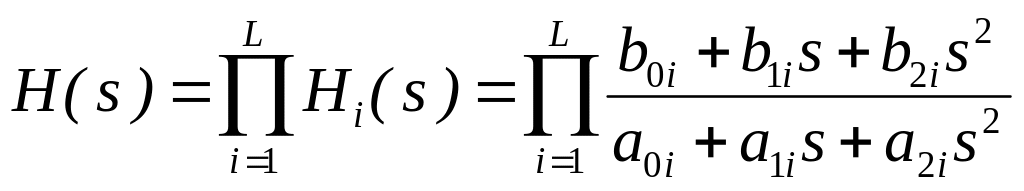 .
.
![]() .
.![]() ,
то из выражения (6) для ПФ системы
получаем её частотную характеристику
,
то из выражения (6) для ПФ системы
получаем её частотную характеристику
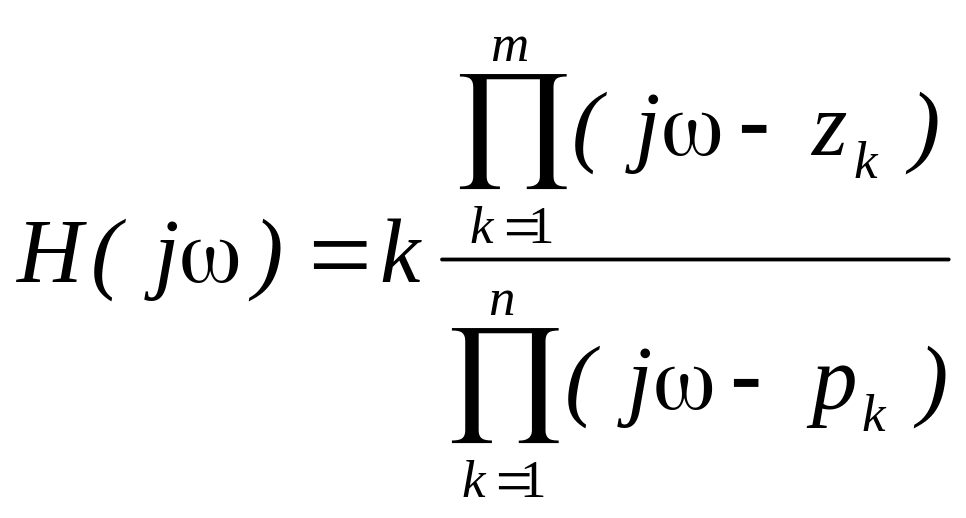 .
.
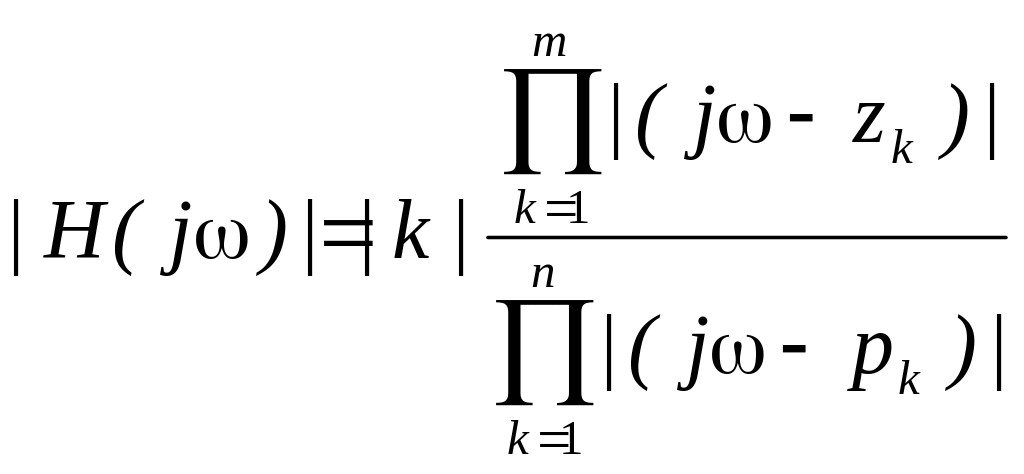 равна произведению/отношению длин
векторов, каждый из которых равен
разности значения частоты и нуля/полюса.
равна произведению/отношению длин
векторов, каждый из которых равен
разности значения частоты и нуля/полюса.
![]()
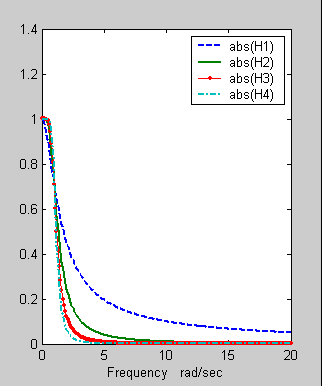
Пример 2. Иллюстрация зависимости
поведения АЧХ системы от количества и
расположения полюсов
Из этого примера очевидно, что увеличение
числа полюсов приводит к более крутому
спаду АЧХ системы, т.е. к улучшению
поведения фильтра (системы). Поэтому
выбор числа и положения полюсов –
основной способ получения фильтра с
необходимой АЧХ.
w=0:0.1:20; % частотная
шкала
% Система 1-го
порядка с одним полюсом
p=-1;
H1=1./(j*w-p);
% Система 2-го
порядка с двумя полюсами p1=-0.707+j*0.707;
p2=-0.707-j*0.707;
H2=1./(j*w-p1)./(j*w-p2);
% Система 3-го
порядка с тремя полюсами
p31=-0.5+j*0.866;
p32=-0.5-j*0.866;
p33=-1;
H3=1./(j*w-p31)./(j*w-p32)./(j*w-p33);
% Система 4-го
порядка с четырьмя полюсами
p41=-0.383+j*0.924;
p42=-0.383-j*0.924;
p43=-0.924+j*0.383;
p44=-0.924-j*0.383
H4=1./(j*w-p41)./(j*w-p42)./(j*w-p43)./(j*w-p44); plot(w,
abs(H1),'--',w,abs(H2), w, abs(H3),'.-',w,abs(H4))
legend('abs(H1)','abs(H2)','abs(H3)',
'abs(H4)' )
xlabel('Frequency rad/sec')