Одностороннее преобразование Лапласа (one sided or unilateral Laplace Transformation)

. (1)

Для функций , т.е. для каузальных функций, оно аналогично двустороннему преобразованию. Обычно какой- либо сигнал (процесс) начинается в конечный момент времени, который можно принять за начало отсчета. Затем сигнал существует в течение какого-то промежутка времени, теоретически до . Поэтому на практике как правило используется одностороннее преобразование Лапласа.

В дальнейшем в этой части курса рассматривается только одностороннее преобразование Лапласа. Нотация ,

x(t) - функция – оригинал, X(s) – функция – изображение.

Преобразование Лапласа имеет смысл только для тех значений s, где интеграл сходится. Если , т.е. функция x(t) возрастает не быстрее экспоненты с показателем a, то преобразование Лапласа сходится для Re(s)> a. Область плоскости s = σ +jω, где преобразование Лапласа сходится, называется областью сходимости (ОС).

Пример 1.

Пример 2. ,

Пример 3. ,

Заметим, что преобразование Фурье для единичной ступенчатой функции u(t) не существует, так как эта функция не удовлетворяет условию абсолютной интегрируемости . Преобразование же Лапласа сходится из-за множителя : .

Пример 4.

. Аналогично .

Пример 5. . Подобные примеры можно продолжить. В специальной литературе существует большое количество справочных таблиц для различных функций – оригиналов и их изображений. Эти таблицы используются для нахождения прямого и обратного преобразований Лапласа.

В MATLAB имеется функция laplace() для символьных (аналитических) вычислений преобразования Лапласа и Ilaplace() для обратного преобразования. Пример:

>> syms a t >> laplace(exp(-a*t)) Результат ans = 1/(s+a).

Свойства преобразования Лапласа

Преобразование Лапласа имеет свойства, аналогичные преобразованию Фурье. Ниже они приведены без доказательства. Сами доказательства аналогичны доказательствам свойств преобразования Фурье (НВПФ), рассмотренным в лекции № 7.

1. Свойство линейности. Если , то .

2. Свойство временного сдвига. Если , то .

3. Свойство сдвига в s – плоскости. Если , то .

4. Свойство временного масштабирования. Если , то .

5. Свойство свертки. Если , то

6. Свойство дифференцирования в временной области. Если , то . Обобщение свойства для производной n –го порядка .

Благодаря этому свойству дифференциальное уравнение может быть преобразовано в алгебраическое уравнение. Далее находится решение алгебраического уравнения и выполняется обратное преобразование Лапласа.

7. Свойство дифференцирования в частотной области. Если , то .

8. Свойство интегрирования во временной области. Если , то .

9. Теорема о начальном значении .

10. Теорема о конечном значении Эти свойства очень часто используются в различных практических задачах, связанных с использованием преобразования Лапласа.

Обратное преобразование Лапласа

Обратное преобразование Лаплас позволяет найти функцию – оригинал x(t) по изображению X(s). Общее выражение обратного преобразования Лапласа

(2)

представляет собой контурный интеграл в комплексной s – плоскости. В большинстве случаев его вычисление - достаточно сложная задача с использованием теоремы о вычетах. На практике для перехода во временную область используются таблицы преобразования Лапласа и вычисления с использованием разложения дробно - рационального выражения X(s) на простые дроби (см. файл «Разложение дробно - рациональной функции на простейшие дроби» в справочно – информационных материалах по курсу).

В Matlab для символьного вычисления обратного преобразования Лапласа служит функция Ilaplace().

Пример. Найдем оригинал для

>> syms s a >> ilaplace(1/(s-a)^2)

ans =

t*exp(a*t)

Передаточная функция линейной непрерывной стационарной системы (лнсс)

Предварительно докажем свойство дифференцирования преобразования Лапласа.

Если . Доказательство: интегрируем по частям

. По условию , при t =0 . Поэтому .

Для нулевых начальных условий (н.н.у.) x(0)=0, поэтому L{x’(t)}=sX(s).

Аналогично рассуждая, получим ,

и для н.н.у. .

Передаточная функция (ПФ) линейной непрерывной стационарной системы –

это отношение преобразований Лапласа выходного и входного сигналов системы при нулевых начальных условиях.

Дифференциальное уравнение ЛНСС .

Возьмем преобразование Лапласа от левой и правой частей уравнения при нулевых начальных условиях.

С учетом свойства дифференцирования и свойства линейности получаем . Отсюда ПФ

(3)

Другое название ПФ (transfer function) – системная функция (system function).

Связь выхода и входа системы в области комплексной переменной s

. (4)

Т.е., преобразование Лапласа выходного сигнала равно преобразованию Лапласа входного сигнала, умноженному на передаточную функцию системы.

Переход во временную область осуществляется с помощью обратного преобразования Лапласа .

Пусть входной сигнал - дельта-функция. Ему соответствует отклик в виде импульсной характеристики (ИХ) системы . В s - плоскости для δ(t) и . Следовательно, связь ИХ и ПФ системы

(5)

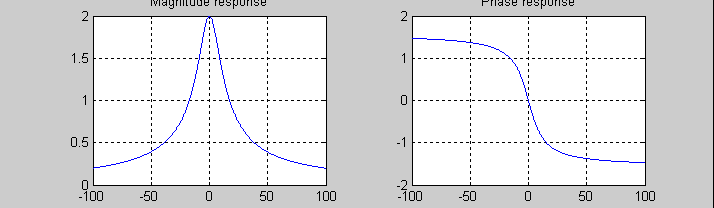
Графики АЧХ, ФЧХ и передаточной функции рассматриваемого фильтра

w=-100:0.1:100; H=20./(10+j*w); plot(w,abs(H)) subplot(121), plot(w,abs(H))

grid, xlabel('Frequency, rad/sec'), title('Magnitude response')

subplot(122), plot(w,angle(H))

grid, xlabel('Frequency, rad/sec'), title('Phase response')

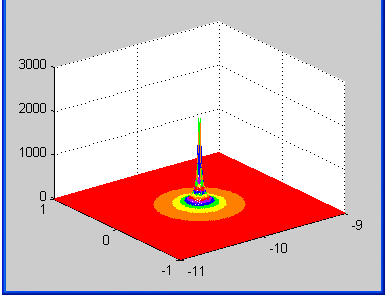
[x,y]=meshgrid(-11:0.01:-9, -1:0.01:1);

s=x+y*j;

H=20./(s+10);

mesh(x,y,abs(H))

Пояснение. Передаточная функция является функцией переменной , состоящей из действительной и мнимой части.

Т.е. - функция 2-х переменных. График её модуля – трехмерный.