
Пользовательская
функция для вычисления ДПФ по выражению
(1)
на
языке
MATLAB:
function
X
= dft(x)
% функция вычисления
дискретного преобразования Фурье X
% обращение y
= dft(x),
x-
вектор сигнала
N = length(x);
X=zeros(N,1);
n = 0:N-1;
for
k=0:N-1
X(k+1) =
sum(exp(-j*2*pi*k*n/N).
*x);
end
Но на практике для
вычисления ДПФ и ОДПФ эта простая
функция применяется редко, а используются
соответственно функции Matlab
fft()
и ifft(),
основанные
на
алгоритмах
быстрого преобразования Фурье
(БПФ).
БПФ – это не отдельная разновидность
преобразования Фурье, это особый быстрый
алгоритм вычисления ДПФ. Функции dft()
и fft()
с точностью до погрешности вычислений
дают одинаковый результат, но они
имеют очень разное время вычисления.
Функция fft()вычисляет
ДПФ в десятки – тысячи раз быстрее, в
зависимости от значения N.
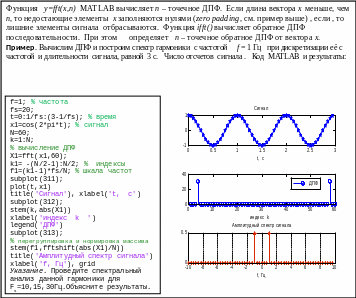
Для представления
сигнала в частотной области необходимо
соответствующее масштабирование шкалы
частот для получения правильных
значений частоты. Пусть последовательность
из N
точек получена дискретизацией сигнала
с частотой отсчетов
Например, если
ДПФ
может быть представлено в матричной
форме как произведение матрицы A
на вектор x
X
= A
x
где x- вектор – столбец
значений сигнала, x’
=
А – матрица преобразования
вектора x в вектор
X, имеющая вид
Выражение для элемента матрицы,
расположенного в n-ом
столбце и m-ой строке,
может быть вычислено по формуле
В Matlab для вычисления
матрицы А служит функция A
= dftmtx(N).
Самостоятельно выполните и проанализируйте
пример A=dftmtx(8).
Матричная запись дает более ясное
представление о характере вычисления
ДПФ.
Из X
= A
x,
как
и из выражения
Вычисления дпф и одпф в matlab
![]() .
Частота Fk
и
порядковый номер (индекс) отсчета k
в частотной
области связаны соотношением (см. (1))
.
Частота Fk
и
порядковый номер (индекс) отсчета k
в частотной
области связаны соотношением (см. (1))![]() k
= 0,1,.., N-1.
k
= 0,1,.., N-1.
![]() - частотное разрешение
анализа.
- частотное разрешение
анализа.![]() ,
то
,
то
![]() .
.Матричная запись дпф
![]()
![]() - вектор-строка,
- вектор-строка,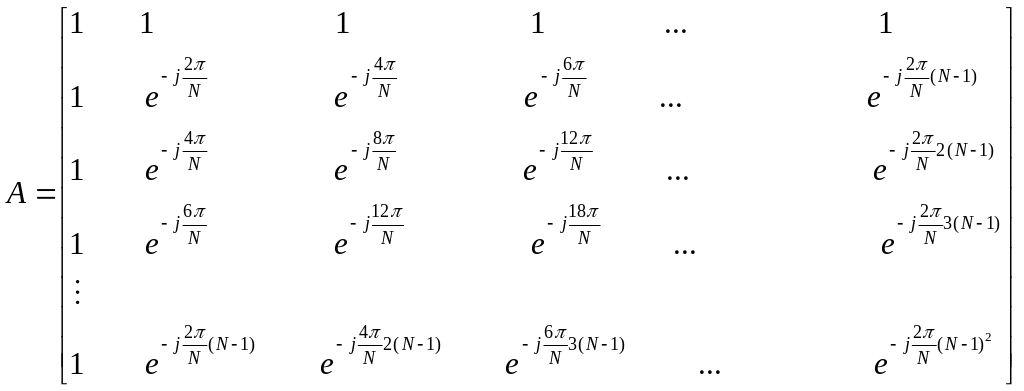
![]()
![]() следует, что прямое вычисление XN[k]
для
требует N2
комплексных умножений и
следует, что прямое вычисление XN[k]
для
требует N2
комплексных умножений и
![]() комплексных
сложений.
комплексных
сложений.
Рассмотрим наиболее
часто используемые на практике свойства
этого преобразования. Часть
из этих
свойств аналогична соответствующим
свойствам НВПФ (лекция № 7).
1. Свойство
периодичности.
ДПФ и ОДПФ, определяемые выражениями
(1) и (2), являются периодическими
последовательностями с периодом N.
Это следует из периодического характера
комплексной экспоненты
Поэтому
Следовательно,
и
Т.о., и прямое и
обратное ДПФ размера
N
являются
периодическими
с периодом N.
2. Свойство
линейности.
Если
Доказательство –
простое, основывается на определении
ДПФ.
Свойство комплексной
сопряженности.
Если x[n]
– действительная последовательность,
то
Свойства дпф
![]() .
.![]()
![]()
![]() .
.![]()
![]() и
и
![]() ,
то
,
то
![]()
![]() .
Доказательство:
.
Доказательство:
![]() .
В то же время
.
В то же время
![]() .
.

N=4
k
Значит,
Поэтому модуль
4. Свойство
симметрии:
Т.е.,
Доказательство:
Следовательно,
Индекс
Следствие:
чтобы получить ДПФ последовательности
x[n],
достаточно вычислить только первые
![]() и
и
![]() .
.![]() - четная функция k,
фаза
- четная функция k,
фаза
![]() - нечетная функция k.
- нечетная функция k.![]()
![]()
![]() .
Умножим правую часть на
.
Умножим правую часть на
![]() .
.![]() .
.
![]() соответствует т.н. частоте
Найквиста:
соответствует т.н. частоте
Найквиста:
![]()
![]() отсчетов
отсчетов
![]() для
для
![]() .
Значения второй половины для
.
Значения второй половины для
![]() можно найти из соображений симметрии,
поскольку
можно найти из соображений симметрии,
поскольку![]()
![]()
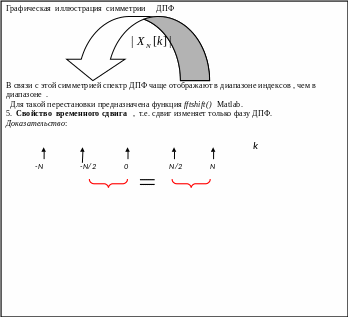
N/2
– индекс
частоты Найквиста
6. Свойство
свертки.
Если
Свойство свертки
широко используется в задачах цифровой
обработки сигналов, фильтрации, анализе
временных рядов и др. приложениях.
ДПФ, как и непрерывное
преобразование Фурье, обладает
дуальностью (двойственности) между
временной и частотной областью. Поэтому
для ДПФ имеется также свойство свертки
в частотной области. Согласно этому
свойству свертке ДПФ сигналов в частотной
области соответствует произведение
последовательностей во временной
области
![]() ,
то
,
то
![]() ,
т.е. дискретной свертке (символ операции
,
т.е. дискретной свертке (символ операции
![]() )
последовательностей во временной
области соответствует произведение
их ДПФ в частотной области.
Доказательство:
)
последовательностей во временной
области соответствует произведение
их ДПФ в частотной области.
Доказательство: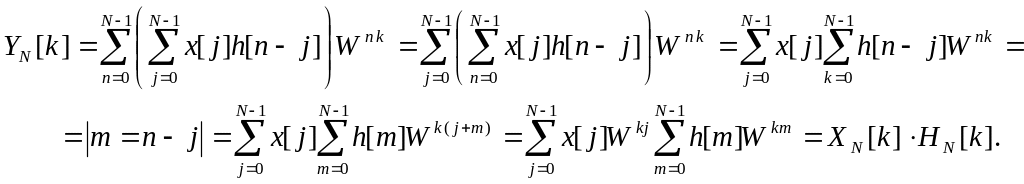
![]()
