
Преобразование
Фурье непрерывного сигнала x(t)
(лекции 6,7 курса)
ставит в соответствие
сигналу x(t)
его спектральную плотность X(jω),
т.е.
Спектральная
плотность X(jω)
характеризует
частотную структуру сигнала x(t).
Но вычислить X(jω)
аналитически можно только для простых
сигналов (функций), например, прямоугольных,
экспоненциальных, треугольных, их
комбинаций и некоторых других сигналов
с простой формой. На практике для
вычисления преобразования Фурье
приходится применять, главным образом,
численные методы, основанные на
дискретном преобразовании Фурье (ДПФ).
Выражение прямого
ДПФ (DFT)
для последовательности x[n]
(сигнала) из N
отсчетов (чисел)
Получим это выражение
из классического преобразования Фурье.
Пусть из непрерывного
по времени сигнала
x(t)
конечной длительности берутся отсчеты
с интервалом TS.
Сигнал равен нулю за пределами интервала
[0, (N-1)TS],
при этом N
– число отсчетов,
TSN
– продолжительность (длина) сигнала.
Преобразование Фурье (НВПФ) такого
сигнала можно представить приближенно
в виде интегральной суммы
Приближенные
значения НВПФ на частотах

Определение и примеры вычисления дискретного преобразования Фурье
![]()
![]() .
.
![]() .
. .
.![]() ,
,
![]() (1)
(1)
Следовательно,
НВПФ сигнала на частотах
приближенно равно
ДПФ, умноженному на значение интервала
отсчетов ТS,
т.е.
Преобразование
Нотация:
Обратное (инверсное)
дискретное преобразование Фурье
(ОДПФ, англ. IDFT)
определяется выражением
Нотация
Выражения (2) и (3)
являются парными относительно
преобразования. Подстановка XN[k]
из (2) в (3) дает снова сигнал x[n].
Это можно строго доказать.
![]()
![]() .
Такая аппроксимация (приближение) тем
точнее, чем меньше интервал отсчетов
TS,
в пределах которого сигнал не должен
существенно измениться.
.
Такая аппроксимация (приближение) тем
точнее, чем меньше интервал отсчетов
TS,
в пределах которого сигнал не должен
существенно измениться.
![]() называется
N
– точечным
дискретным
преобразованием Фурье
(ДПФ, англ. discrete
Fourier
transform,
DFT)
или просто ДПФ последовательности
(сигнала) x[n],
n
- номер отсчета.
Здесь k
– индекс значения ДПФ в частотной
области (индекс частоты). С использованием
для комплексной экспоненты обозначения
называется
N
– точечным
дискретным
преобразованием Фурье
(ДПФ, англ. discrete
Fourier
transform,
DFT)
или просто ДПФ последовательности
(сигнала) x[n],
n
- номер отсчета.
Здесь k
– индекс значения ДПФ в частотной
области (индекс частоты). С использованием
для комплексной экспоненты обозначения
![]() его можно записать более компактно
в виде
его можно записать более компактно
в виде![]() . (2)
. (2)![]() ,или
,или
![]() ,
или
,
или
![]() ,
N
– длина (размер) ДПФ.
,
N
– длина (размер) ДПФ.![]() .
(3)
.
(3)![]() или
или
![]() .
.
Преобразование Фурье непрерывного
сигнала x(t)
ставит в соответствие функции x(t)
её спектральную плотность X(jω).
Для сигналов дискретного аргумента
x(nΔt)=x[n],
Δt = 1/FS
преобразование Фурье имеет некоторые
особенности и свойства, обусловленные
дискретизацией. Эту разновидность
называют дискретно – временным
преобразованием Фурье (ДВПФ).
Для его получения представим интеграл
в виде приближения - интегральной суммы
Здесь
Для
Правая часть получившегося выражения
и есть дискретно – временное
преобразование Фурье (англ. Discrete
Time Fourier
Transform, DTFT)
дискретного сигнала
Оно имеет для дискретных сигналов x[n]
тот же смысл, что обычное прямое
преобразование Фурье для непрерывных
сигналов x(t).
Нотация
Определение дискретно – временного преобразования Фурье
![]()
![]() .
.![]() имеет смысл интервала отсчетов.
имеет смысл интервала отсчетов.![]()
![]() .
.
![]() ,
которое определяется следующим
образом
,
которое определяется следующим
образом
![]() – прямое ДВПФ, выражение анализа.
– прямое ДВПФ, выражение анализа.![]() .
.
Если сравнить
выражение (2) с полученным в лекции 5
выражением коэффициента ДВРФ
то получим, что
ДПФ XN[k]
в общем случае
– комплексное выражение, имеющее
действительную и мнимую часть, т.к.
При этом
Пример 1.
Найдем ДПФ единичного импульса. По
сравнению с теоретическим определением
единичного импульса здесь предполагаем
последовательность конечной длины
N
ДПФ такого сигнала
Пример 2.
Найдем ДПФ сигнала
![]() ,
(4)
,
(4)![]() ,
т.е. XN[k]
и сk
отличаются только константой - множителем
N.
,
т.е. XN[k]
и сk
отличаются только константой - множителем
N.![]() .
Его можно представить в алгебраической
или показательной (экспоненциальной)
форме :
.
Его можно представить в алгебраической
или показательной (экспоненциальной)
форме :
![]() - ДПФ - амплитудный спектр сигнала
x[n],
- ДПФ - амплитудный спектр сигнала
x[n],![]() - ДПФ - фазовый
спектр x[n].
- ДПФ - фазовый
спектр x[n].![]()
![]() ,
,
![]() - равно константе 1.
- равно константе 1.![]() для длин N
= 5 и N
= 7.
а) N
= 5
для длин N
= 5 и N
= 7.
а) N
= 5
![]()
Для k
от от 0 до
4 получим

![]()
|X5[k]|
Амплитудный спектр
Фазовый спектр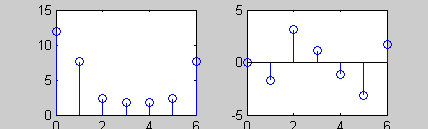
X7[k]
Пример
3.
Определим ДПФ сигнала показательного
сигнала
(функция an
- собственная функция ЛДС)
По формуле суммы
конечной геометрической прогрессии
Сигнал
Амплитудный спектр
Фазовый спектр
Другие примеры
вычисления ДПФ см. в файле «Задачи_4»
методических материалов по курсу.
Обучающие и
демонстрационные материалы по ДПФ в
Интернет:
http://www.fourier-series.com/fourierseries2/DFT_tutorial.html
Демонстрация
MATLAB: Demos|Toolboxes|Signal
Processing|Transforms|Discrete Fourier Transform
![]()
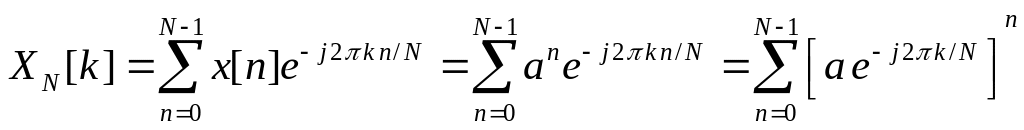 .
.![]() получаем для
получаем для
![]()
![]() .
Графики сигнала и спектров для
N=16,
a=0,9:
.
Графики сигнала и спектров для
N=16,
a=0,9:
