1.3.4. Моменты функций от случайных величин
Очевидно, что любая нетривиальная функция от случайной величины есть также случайная величина. Пусть определена взаимно однозначная функция = f(). Если случайная величина задана в виде
,
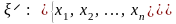то случайная величина будет представлена своими значениями и их вероятностями следующим образом:
,
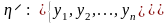где
.
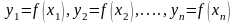Моменты случайной величины записываются очевидным образом:
начальные
;
центральные
.
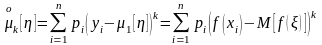Рассмотрим полезный для приложений частный случай линейной функции случайной величины, а именно функцию = a + b.
.
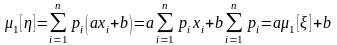Полученное выражение показывает, что математическое ожидание линейной функции от случайной величины есть функция от математического ожидания этой величины:
.
Найдем второй центральный момент, то есть дисперсию этой функции:
.
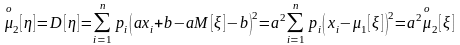В терминах и в обозначении дисперсий это соотношение имеет вид:
D[a
+ b]
=
.
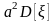Как и следовало ожидать, из этого выражения следует, что смещение значений случайной величины не влияет на ее дисперсию.
Пусть
.
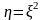Тогда
.
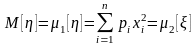Пусть
.
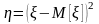Тогда 
.
1.3.5. Производящая функция моментов
Производящей функцией моментов случайной величины называется математическое ожидание функции y() = exp(), где – аргумент производящей функции моментов:
.
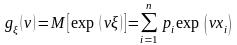Производящая функция моментов обладает рядом полезных свойств.
1)
;
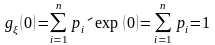2)
Первая производная от
по аргументу
:
,
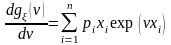при
= 0 получим
;
3) Вторая производная от по аргументу :
,
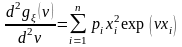при
= 0 получим
;
4) k -я производная от по аргументу :
,
при
= 0 получим
.
Таким образом, чтобы получить значение k-го начального момента, достаточно продифференцировать производящую функцию моментов k раз по и подставить в полученную производную = 0.
П р и м е р. Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.
.
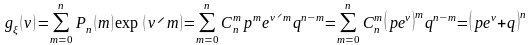Первая производная от по
.
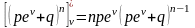Вторая производная от по
.
Вычислим эти производные при = 0:
,
.
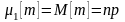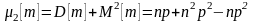Окончательно получим: M[m] = np, D[m] = np(1 – p) = npq.
Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают.
З а м е ч а н и е о сходимости распределений вероятности и производящих функций моментов.
Пусть
имеется последовательность распределений
вероятностей дискретной случайной
величины
.
Пусть
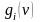– производящие функции соответствующих
распределений
из этой последовательности, которые
также образуют последовательность
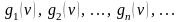
Если
последовательность
сходится, имеет предел и пределом этой
последовательности является распределение
,
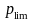то последовательность
также сходится, имеет предел, и ее
пределом является производящая функция
моментов предельного распределения.
Справедливо и обратное утверждение.
Обратим внимание на то, что конструкция производящей функции моментов близка конструкции обратного дискретного преобразования Фурье, отсюда вытекают полезные свойства производящих функций моментов и близость их свойств свойствам дискретного преобразования Фурье.